更新日志
20250122:开工。
思路
我们定义 \(z_i\) 表示从 \(i\) 开始的后缀与整个字符串的最长公共前缀长度。
考虑它的作用,假如我们要字符串匹配,将模式串接在前面并以特殊字符分隔,然后 \(O(n)\) 遍历原串,当 \(z_i=|T|\)(\(T\) 为模式串)时,这个位置就是一个匹配上的位置的开始。
然后我们考虑如何快速求出 \(z\)。
我们考虑储存最大的 \(i+z_i\) 信息,称作 \(zbox\),也就是匹配上的最大右边界。比如:
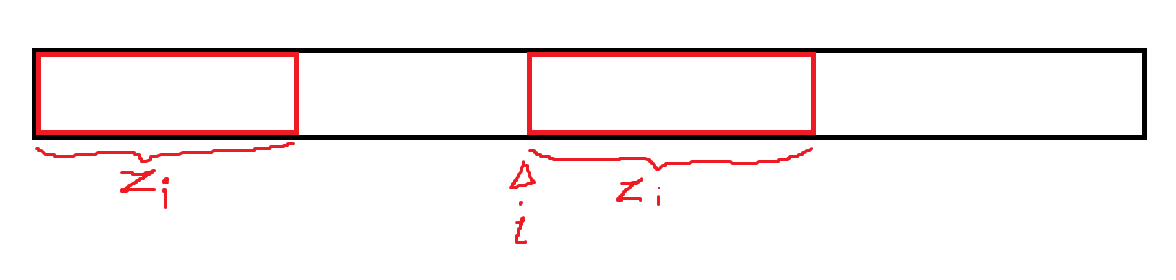
假如这一段(右侧,左边的是与其相同部分)就是 \(zbox\)。
下面我们考虑 \(i\),也就是当前需要的。
如果 \(i\) 位于 \(zbox\) 内(在 \(zbox\) 外暴力即可),那我们可以找出其在左侧的对应位置。
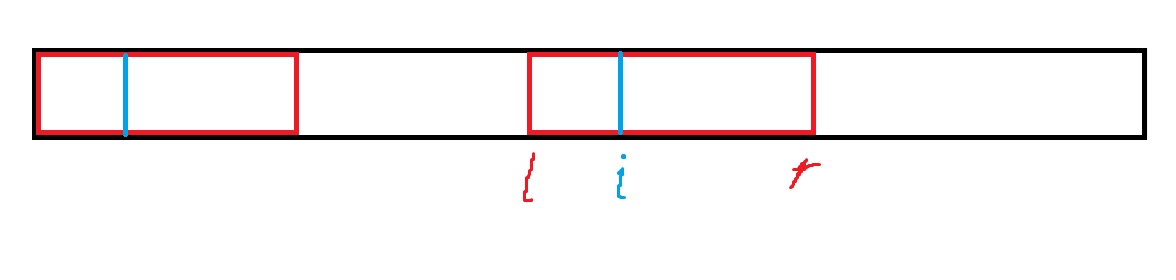
如果对应位置的 \(z\) 在对应的 \(r\) 以内(相等不算),那么显然 \(z_i=z_j\)(\(j\) 为对应位置),因为下一位是相等的,上一段不行,这一段一样的不行。
不然,下一位就是不相等的,就得暴力了。但是,我们可以把 \(zbox\) 以内的部分直接 \(O(1)\) 加过来。
更新 \(zbox\) 部分就不说了,判右边界即可。
这样不难发现每个点只会被暴力一次,复杂度 \(O(n)\)。
模板
string a,b;
int z[N],l,r;
void getz(string s){z[0]=l=r=0;repl(i,1,s.size()){if(i<=r&&z[i-l]<r-i+1)z[i]=z[i-l];else{z[i]=max(0,r-i+1);while(i+z[i]<s.size()&&s[i+z[i]]==s[z[i]])z[i]++;}if(i+z[i]-1>r)l=i,r=i+z[i]-1;}
}
例题
LG5410
代码
#include<bits/stdc++.h>
using namespace std;typedef long long ll;
typedef unsigned long long ull;
typedef __int128 i128;
typedef double db;
typedef long double ld;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
typedef pair<int,ll> pil;
typedef pair<ll,int> pli;
template <typename Type>
using vec=vector<Type>;
template <typename Type>
using grheap=priority_queue<Type>;
template <typename Type>
using lrheap=priority_queue<Type,vector<Type>,greater<Type> >;
#define fir first
#define sec second
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define chmax(a,b) a=max(a,b)
#define chmin(a,b) a=min(a,b)
#define rep(i,x,y) for(int i=(x);i<=(y);i++)
#define repl(i,x,y) for(int i=(x);i<(y);i++)
#define per(i,x,y) for(int i=(x);i>=(y);i--)const int inf=0x3f3f3f3f;
const ll INF=0x3f3f3f3f3f3f3f3f;
const int mod=998244353;const int N=4e7+5;string a,b;
int z[N],l,r;
void getz(string s){z[0]=l=r=0;repl(i,1,s.size()){if(i<=r&&z[i-l]<r-i+1)z[i]=z[i-l];else{z[i]=max(0,r-i+1);while(i+z[i]<s.size()&&s[i+z[i]]==s[z[i]])z[i]++;}if(i+z[i]-1>r)l=i,r=i+z[i]-1;}
}ll ans1,ans2;int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>a>>b;a=b+' '+a;getz(a);z[0]=b.size();repl(i,0,b.size())ans1^=((ll)(i+1)*(z[i]+1));repl(i,b.size()+1,a.size())ans2^=((ll)(i-b.size())*(z[i]+1));cout<<ans1<<"\n"<<ans2;return 0;
}