### 枚举与搜索
- 枚举:框定一个范围,遍历其中的所有东西。比如枚举左右端点成为一个区间。
- 搜索:从一个初始状态出发,一步一步走到相邻的状态,遍历能走到的所有东西。比如走迷宫。
本质都是**用各种各样的策略去找东西**
#### 枚举优化
1. 改变枚举对象:比如说从枚举左右端点改成枚举最值,从枚举因数改成枚举倍数。
2. 改变枚举顺序:比如说倒着枚举。
3. 减少枚举量:比如说通过观察发现有东西是不需要枚举的。
---
##### 例1
$n$ 的序列,有 $c_i(1\le c_i\le n)$ 个颜色,对于所有区间颜色个数求和。
考虑对于每一个颜色 $c[i]$,其贡献由以下两部分组成:
- 从当前位置 $i$ 到之前出现该颜色的位置之间的区间长度。
- 当前区间长度,即从位置 $i$ 到数组末尾的长度。
第二个就是 $n - i + 1$,第一个就是用当前位置的颜色减去颜色 $ c[i] $ 从 $1$ 到 $ i-1 $ 的位置已经出现的次数,即 $i - \text{vis}[c[i]]$。
求得就是
$$
\sum_{i=1}^{n} (i - \text{vis}[c[i]]) (n - i + 1)
$$
代码:
过于简单,略
---
##### 例2
给定 $n$ 个正整数 $a_i$,请你在其中选出三个数 $i, j, k$($i \ne j$,$i \ne k$,$j \ne k$),使得 $(a_i + a_j) \bmod a_k$ 的值最大。
暴力是 $O(n^3)$,考虑优化首先 $k$ 可以在for循环最外层。
发现
1. 相同出现过的数字只枚举一次即可。
2. 从大到小枚举 $a_k$, 然后记录一个答案 $p$。一旦 $a_k\le p$ 则不再枚举。
---
##### 例3
有 $n$ 个人正在打模拟赛,模拟赛有 $n$ 道题目。
定义第 $i$ 个人会的题目的集合为 $S_i$ ,即当 $S_x\cap S_y\neq\varnothing\land S_x\not\subseteq S_y\land S_y\not\subseteq S_x$ 时,第 $x$ 人和第 $y$ 人会讨论。
本质是让你找集合,发现YES难,**正难则反**,判断NO。
如图,$vis[i]$ 表示上个会 $i$ 道题人的序号,判断即可。
---
### DFS与BFS
- DFS:用递归实现,“一条路走到黑”,好写。
- BFS:用队列+循环实现,“大水漫灌”,适合一部分“最小化”问题,例如熟悉的最短路问题。
搜索过程其实就是**状态转移**。
#### 可行性剪枝
观察:朴素搜索太蠢了!一些明显会使得接下来不合法的策略可以舍弃。也就是在搜索树上“回头”,避开了一些无用的分支,“剪枝”因此得名。
简单来说,如果你一眼望过去全都不合法,那就不要继续走下去了。
---
##### 例1
把一个正整数 $n$ 拆分为 $m$ 个 $<=k$ 的正整数相加,求所有方案。例如 $11 = 1 + 1 + 4 + 5$ 就是把 $11$ 拆分为 $4$ 个数相加。(要求数字从小到大排序)
朴素的搜索:
```cpp
void dfs(int num, int i, int last){
if(i == m + 1 && num == 0){
for(int i = 1; i <= m; i++)cout << dc[i] << ' ';
cout << '\n';
return ;
}
for(int d = last; d <= k; d++){
if(num - d >= 0)
dc[i] = d,dfs(num - d, i + 1, d);
}
```
考虑去掉“一眼望过去”显然不合法的状态。
```cpp
void dfs(int num, int i, int last){
if(i == m + 1 && num == 0){
for(int i = 1; i <= m; i++)cout << dc[i] << ' ';
cout << '\n';
return ;
}
for(int d = last; d <= k; d++){
if(num - d * (m - i + 1) >= 0 && num - d - k * (m - i) <= 0)
dc[i] = d,dfs(num - d, i + 1, d);
}
```
---
### 启发式搜索与A*
观察2:
一些状态比另一些状态“更容易”到达最优解。如果我们能给每一个状态评一个价值,就能够优先走那些“更好”的状态。
具体来说,使用一个数 $h$ 去代表当前这个状态到达最终状态的理论最优秀代价。那么它目前的代价 $g$ 加上这个理论最优代价 $h$ 就得到了这个点的估计价值 $f=g+h$。
有了这个 $f$ 我们能干点啥?
1. 如果 $f >$当前 $ans$ ,那么你还愣着干什么,赶快回头!(最优性剪枝)
2. 如果我能走到好多个状态,那肯定是优先走f更小的那个啊!(A*)
如果把 $h=0$,就变成了dijskra。
---
##### 例1
首先设计一个最朴素的搜索:先枚举从下往上数第一层的半径,然后一层一层向上搜索。
接下来开始剪枝:
可行性剪枝:从上往下第 $i$ 层的高和半径至少为 $i$ 。体积的最小值和最大值都可以计算。
最优性剪枝:将 $h$ 设置为尽可能小地放蛋糕,不考虑体积为 $N\pi$ 这一限制的情况下,得到的代价。
加入这两个剪枝之后足以通过本题。
```cpp
#include<bits/stdc++.h>
using namespace std;
int n, m;
const int manx = 1e6;
int ans = 987654321;
int mins[manx],minv[manx];
inline void dfs(int c,int v, int s,int h,int r) {
if(c == 0){
if(v == n) ans = min(ans ,s);
return;
}
if(v + minv[c] > n) return;
if(s + mins[c] > ans) return;
if(s + 2 *(n-v) / r > ans ) return;
for (int i = r - 1; i >= c; --i)
{
if(c == m) s = i * i;
int Maxh = min(h - 1,(n - v - minv[c - 1])/(i * i));
for (int j = Maxh; j >= c; --j)
dfs(c - 1, v + i * i * j, s + 2 * i * j,j,i);
}}
int main() {
scanf("%d%d", &n, &m);
int MaxR = sqrt(n);
for(int i = 1;i <= n; i++){
minv[i] = minv[i-1] + i * i * i;
mins[i] = mins[i-1] + 2 * i * i;
}
dfs(m,0,0,n,MaxR);
if(ans == 987654321)
cout<<-1<<endl;
else cout<<ans<<endl;
return 0;
}
```
---
### 记忆化搜索
如果你走迷宫,走进一个屋子,经历了一番波折(dfs)后终于返回这个屋子,在墙上写下“从这里走到终点至少需要100步”,那么等你下次走到相同的屋子时,你大可不必再走一遍,而是直接掉头走人。
这便是“记忆化搜索”在干的事情,我们开一个数组 $res[u]$,记录 $u$ 这个状态出发到达最终状态的代价。那么我们走到每个点的次数就会大大减少了。
但是另一方面,如果你拿着一把钥匙重新走进了这个房间,你可能就不能根据房间上的字去做判断了——手中的钥匙改变了之后有可能作出的判断,也就是动态规划里提到的“后效性”。
---
##### 例1
记忆化搜索模板题,我们以每一个位置为起点开始搜索。
记 $f[x][y]$ 表示以 $(x,y)$ 为起点,最长的滑雪路径。
```cpp
#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <vector>
#include <cstring>
#include <cstdio>
#include <set>
#include <map>
#include <unordered_map>
#include <bitset>
using namespace std;
const int MAXX = 1e5 + 10, MAXN = 1e9 + 10;
inline int read(){
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int n, m;
int h[233][233], f[233][233];//f[i][j]代表从(i, j)这个位置出发 最远能滑多远
bool g[233][233];//g[i][j]代表f[i][j]算过没
int dx[10] = {-1, 1, 0, 0};//上下左右
int dy[10] = {0, 0, -1, 1};//dx[i], dy[i]代表的是在第i个方向下x的坐标和y坐标的偏差值
const int M = 250 * 250;
pair<int, int> z[M];//z[i]代表一个坐标
bool cmp(pair<int, int> a, pair<int, int> b){
return h[a.first][a.second] > h[b.first][b.second];
}
int main(){
n = read(), m = read();
int k = 0;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
h[i][j] = read();//每个位置的高度
k++;
z[k] = make_pair(i, j);
}
}
sort(z + 1, z + k + 1, cmp);
for(int a = 1;a <= k;a++){
int i = z[a].first;
int j = z[a].second;
//取出当前坐标
//int h = ::h[i][j];
//取出当前坐标高度
f[i][j] = max(f[i][j], 1);
for(int d = 0;d < 4;d++){
int x = i + dx[d];
int y = j + dy[d];
//从 (i,j)沿着方向d走一格会走到(x, y)
if(x >= 1 && x <= n && y >= 1 && y <= m)//判断(x, y)是否合法
if(h[i][j] > h[x][y])//(i, j)高度比(x, y)高度更高
f[x][y] = max(f[x][y], f[i][j] + 1);
}
}
int ans = -1;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
ans = max(ans, f[i][j]);
cout << ans << endl;
return 0;
}
```
---
#### 双向广搜
观察3:对一张图的广搜而言,单向搜索不如“双向奔赴”。因此我们不妨从起点和终点同时或者分别开始广搜,接着检查是否到达了相同的点。
稍微分析一下这样做的复杂度:假设搜索树分叉为 $k$ ,从起点到终点要m步,那么双向广搜实际上将一个 $O(k^m)$ 的朴素广搜变成了一个 $O(k^{m/2})$ 的搜索,复杂度直接开方!
与这个搜索类似的算法叫做meet in middle。

---
### 枚举子集
有些时候我们写搜索其实就是为了枚举所有可能的情况,此时如果一个for循环就能解决我们的问题,那么会极大地提高代码书写与运行的效率。
枚举子集就是这样的一个情况。
考虑一个集合 {1,2,3,…,n},我们需要枚举这个集合的所有子集,怎么办?
```cpp
void dfs(int idx) {
if (idx == n + 1) {
// do something...
return ;
}
num[++tot] = idx;
dfs(idx + 1);
num[tot--] = 0;
dfs(idx + 1);
}
```
```cpp
void subset() {
for (int s = 0; s < (1 << n); s++) {
for (int i = 0; i < n; i++) {
if (s >> i & 1) {
// do something...
}
}
}
}
```
上述是朴素的暴力。
将一个数视为一个二进制串, $ 0 $ 表示没选 $ 1 $ 表示选了,那么一个 $ [0,2^n) $ 范围内的数,就会唯一对应一个长度为n的二进制串,也就唯一对应一个选择方案。
使用位运算 $ (s>>i)\&1 $ 获取这个二进制串从小到大的第 $ i(0≤i<n) $ 位。
复习一下位运算:两个选法并起来,交起来,把第i位设置为 $ 0/1 $ ,让第 $ i $ 位从 $ 0 $ 变 $ 1 $ ,从 $ 1 $ 变 $ 0 $ 。判断子集 $ A $ 是否包含子集 $ B $ 。
判断子集 $ A $ 是否包含子集 $ B $有两种方法。
1. `if(a & b == a)` 即 $ a $ 交 $ b $ 为 $ b $
2. `if(a | b == b)` 即 $ a $ 并 $ b $ 为 $ a $
另外还有一个操作是枚举子集的子集。
```cpp
void subsubset() {
for (int s = 0; s < (1 << n); s++) {
for (int ss = s; ss; ss = (ss - 1) & s) {
// do something...
}
}
}
```
如图:


#### 复杂度
朴素dfs: $ O(2^n) $
枚举子集: $ O(2^n) $
枚举子集的子集: $ O(3^n) $
提问:现在 $ n=26 $ ,求所有子集的异或和之和。 $ (2^26 * 26) $ 过不去哦~
答案:使用 $ dfs $ ,或者使用 $ \text{lowbit}(x) = x \& (-x) $ 获得 $ x $ 的最低位。
```cpp
int log[(1 << 25) + 1]
for (int i = 0; i <= 25; i++) {
log[1 << i] = i;
}
int lowbit(int x) { return x & (-x);
}
int f[(1 << 26)]; // 这个数组 f[S]表示 S 中所有数的^
// a[i] 表示第i个数。
int ans = 0;
for (int s = 1; s < (1 << n); s++) {
f[s] = f[s - lowbit(s)] ^ a[log[lowbit(s)]];
ans += f[s];
}
cout << ans;
int wupin[1232133], tot;
void dfs(int cur) {
if (cur == n + 1) {
// 搜完了
return ;
}
wupi[++tot] = cur;
dfs(cur + 1);
tot--;
dfs(cur + 1);
}
```
---
### 序列分治&逆序对
所谓归并排序,就是先递归到左边,排一下序,再递归到右边,排一下序,最后两个有序序列通过双指针合并,就得到答案。
而求逆序对,就是在每一层中考虑越过分界点的所有逆序对。
因为两边的序列已经有序了,我们只需要一个双指针就可以统计出所有逆序对了。
---
### 序列分治
其实所谓序列分治,就是像归并排序一样的思路:
1. 合并:将分治的两边处理完之后,在本层合并,有时候就是简单相加。
2. 统计:统计完分治两边的答案后,统计跨过分治中心的答案。
这一部分内容会在接下来的数据结构中有详细的拓展。
另外,之所以加上“序列”的前缀,是因为实际上还有“点分治”,“根号分治”等等更广义的分治,大家将会在以后学到。
---
##### 例1
给定平面上 $n$ 个点,找出其中的一对点的距离,使得在这 $n$ 个点的所有点对中,该距离为所有点对中最小的
首先,把所有点按照 $x$ 坐标从小到大排序,紧接着,考虑分治。
我们将整个平面关于分治中心的横坐标竖着分成两半,然后分别对左右两边进行递归,得到答案 $d$,接着,考虑跨越分治中心的点对。
1. 如果点 $ i $ 距离分治中心的距离比d大,那么它一定不会对答案造成贡献。
2. 如果点 $ i $ 与点 $ j $ 对答案造成贡献,那么它们的纵坐标之差不会大于d。
3. 如果两个点 $ i $ 和点 $ j $ 在同侧,那么它们的距离一定大于等于 $ d $。
于是,我们考虑把所有满足 $ 1 $ 条件的点按照纵坐标排序,紧接着对于每一个点 $ i $,能够与它作贡献的点不会多于 $ 5 $ 个,暴力枚举即可。
如图


---
##### 例2
给定一个 $n \times n$ 的棋盘,其中有 $n$ 个棋子,每行每列恰好有一个棋子。
对于所有的 $1 \leq k \leq n$,求有多少个 $k \times k$ 的子棋盘中恰好有 $k$ 个棋子,输出其总和。
$n \le 3 \times 10^5$。
把它转化成一个排列,求所有满足:$max(l~r)-min(l~r) = r-l$的排列数量。
我们考虑分治:每次只需要统计跨过区间中点的所有区间,那么我们只需要对于每个 $l$,找到所有满足条件的r即可。
将区间分为四类:最大最小值均在左侧,均在右侧,最大值在左而最小值在右,以及最大值在右而最小值在左。
如果是前两类,相当于另一个端点的前缀最大/最小值不能大于/小于某个数,这个限制是简单的。
如果是后两类,以第三类为例,我们枚举左端点,则右端点的最大值要比左端点的小,而右端点的最小值要比左端点的小,因此呈现出个区间,我们需要对于每一个l统计答案,开一个桶即可。
```cpp
#include <cstdio>
#include <cstring>
#include <algorithm>
typedef long long ll;
const int N = 3e5 + 9;
int n, p[N], mx[N], mn[N], buk[N << 1];
#define mid (l + r >> 1)
ll cdq(int l, int r) {
if (l == r) return 1;
ll ret = cdq(l, mid) + cdq(mid + 1, r);
mx[mid] = mn[mid] = p[mid];
for (int i = mid - 1; i >= l; --i) mx[i] = std::max(mx[i + 1], p[i]), mn[i] = std::min(mn[i + 1], p[i]);
mx[mid + 1] = mn[mid + 1] = p[mid + 1];
for (int i = mid + 2; i <= r; ++i) mx[i] = std::max(mx[i - 1], p[i]), mn[i] = std::min(mn[i - 1], p[i]);
int j;
for (int i = l; i <= mid; ++i) {
j = i + mx[i] - mn[i];
if (j <= r && j > mid && mx[j] < mx[i] && mn[j] > mn[i]) ++ret;
}
for (int i = mid + 1; i <= r; ++i) {
j = i - mx[i] + mn[i];
if (j >= l && j <= mid && mx[j] < mx[i] && mn[j] > mn[i]) ++ret;
}
int k = mid + 1; j = mid + 1;
for (int i = mid; i >= l; --i) {
while (j <= r && mn[j] > mn[i]) buk[j - mx[j] + n]++, ++j;
while (k < j && mx[k] < mx[i]) buk[k - mx[k] + n]--, ++k;
ret += buk[i - mn[i] + n];
}
while (k < j) buk[k - mx[k] + n]--, ++k;
k = mid, j = mid;
for (int i = mid + 1; i <= r; ++i) {
while (j >= l && mn[j] > mn[i]) buk[j + mx[j]]++, --j;
while (k > j && mx[k] < mx[i]) buk[k + mx[k]]--, --k;
ret += buk[i + mn[i]];
}
while (k > j) buk[k + mx[k]]--, --k;
return ret;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
int r, c;
scanf("%d %d", &r, &c);
p[r] = c;
}
printf("%lld\n", cdq(1, n));
return 0;
}
```
---
### 贪心
所谓贪心其实就是不断地找当前的最优解,最后发现刚刚好是全局最优解!
所以贪心也是一种搜索,只不过我们每次只走眼下最好的一条路,因此如何合理地说明(众所周知,OI不需要证明,但是我们需要感受)眼下最好的路(局部最优解)一定可以带领我们走向答案(全局最优解)就是我们需要考虑的。
因此我们做贪心题的时候,做的事情是:
1. 找到一个贪心算法
2. 检验它的正确性
我们可以通过例题总结一下常见的贪心套路。
---
##### 例1
在一个果园里,多多已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。
每一次合并,多多可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。可以看出,所有的果子经过 $(n - 1)$ 次合并之后, 就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。
因为还要花大力气把这些果子搬回家,所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为 $1$,并且已知果子的种类数和每种果子的数目,你的任务是设计出合并的次序方案,使多多耗费的体力最少,并输出这个最小的体力耗费值。
思路:
选择让最小果实的先合并。
---
##### 例2
春春幼儿园举办了一年一度的“积木大赛”。今年比赛的内容是搭建一座宽度为 $n$ 的大厦,大厦可以看成由 $n$ 块宽度为 $1$ 的积木组成,第 $i$ 块积木的最终高度需要是 $h_i$。
在搭建开始之前,没有任何积木(可以看成 $n$ 块高度为 $0$ 的积木)。接下来每次操作,小朋友们可以选择一段连续区间 $[l, r]$,然后将第 $L$ 块到第 $R$ 块之间(含第 $L$ 块和第 $R$ 块)所有积木的高度分别增加 $1$。
小 M 是个聪明的小朋友,她很快想出了建造大厦的最佳策略,使得建造所需的操作次数最少。但她不是一个勤于动手的孩子,所以想请你帮忙实现这个策略,并求出最少的操作次数。
思路:每次选择一个区间,左右两边能延伸就延伸。
---
##### 例3
现在各大 oj 上有 $n$ 个比赛,每个比赛的开始、结束的时间点是知道的。
yyy 认为,参加越多的比赛,noip 就能考的越好(假的)。
所以,他想知道他最多能参加几个比赛。
由于 yyy 是蒟蒻,如果要参加一个比赛必须善始善终,而且不能同时参加 $2$ 个及以上的比赛。
思路:
按右端点排序每次能选就选。
---
##### 例4
线段完全覆盖:
思路:
按左端点排序每次选能选的当中右端点最长的。
---
##### 例5
区间点覆盖
思路:
区间按右端点排序,每次取第一个没有被覆盖的线段的右端点。
---
##### 例6
给出一个长度为 $n$ 的序列 $a$,选出其中连续且非空的一段使得这段和最大。
思路:
每次能选则选,和0取max。
---
##### 例7
恰逢 H 国国庆,国王邀请 $n$ 位大臣来玩一个有奖游戏。首先,他让每个大臣在左、右手上面分别写下一个整数,国王自己也在左、右手上各写一个整数。然后,让这 $n$ 位大臣排成一排,国王站在队伍的最前面。排好队后,所有的大臣都会获得国王奖赏的若干金币,每位大臣获得的金币数分别是:排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数,然后向下取整得到的结果。
国王不希望某一个大臣获得特别多的奖赏,所以他想请你帮他重新安排一下队伍的顺序,使得获得奖赏最多的大臣,所获奖赏尽可能的少。注意,国王的位置始终在队伍的最前面。
思路:
交换相邻两项计算权值。
---
##### 例8
Jasio 是一个只有三岁的小男孩,他喜欢玩玩具车。他有 $n$ 辆玩具车被保存在书架上。
架子上的玩具车 Jasio 拿不到,但地板上的他可以拿到。Jasio 的母亲会帮 Jasio 拿架子上的玩具车到地板上。
地板最多只能放 $k$ 辆玩具车。
当地板已经放了 $k$ 辆玩具车时,Jasio 的母亲都会从地板上先拿走一个玩具车放回书架,再拿来 Jasio 想要的玩具车。
现在 Jasio 一共想依次玩 $p$ 个玩具车,问 Jasio 的母亲最少需要拿几次玩具车。(只算拿下来的,不算拿上去的)
贪心策略:每次放回去接下来最晚用到的玩具车。
怎么确定每个玩具车接下来第一次用是什么时间?
记数组next[i]表示第i个位置与它相同的下一个位置是哪个位置,这个倒着扫一遍就可以预处理出来。
接下来只需要维护一个堆,不过我们需要让堆支持删除,但是这个没必要,因为有新的next[]在,旧的next[]就不会来到堆顶,因此我们让它留在那里就行,只需要k++即可。
```cpp
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
const int N = 5e5 + 9;
int n, k, p, a[N], b[N], nxt[N], dist[N];
struct Node {
int id, val;
Node(int id_ = 0, int val_ = 0) : id(id_), val(val_) {}
bool friend operator<(Node a, Node b) { return a.val < b.val; }
};
std::priority_queue<Node> q;
int vis[N];
int main() {
scanf("%d %d %d", &n, &k, &p);
for (int i = 1; i <= p; ++i) {
scanf("%d", &a[i]);
nxt[b[a[i]]] = i;
b[a[i]] = i;
}n
for (int i = 1; i <= p; ++i) if (!nxt[i]) nxt[i] = 0x3f3f3f3f;
int ans = 0, add = 0;
for (int i = 1; i <= p; ++i) {
if (vis[a[i]]) {
++k;
q.push(Node(i, nxt[i]));
continue;
}
if (q.size() < k) { ++ans; q.push(Node(i, nxt[i])); vis[a[i]] = 1; continue; }
Node ret = q.top();
q.pop();
++ans;
vis[a[ret.id]] = 0;
vis[a[i]] = 1;
q.push(Node(i, nxt[i]));
}
printf("%d\n", ans);
return 0;
}
```
---
### 二分
如果想要写对二分,就要认识到二分本质上是**在做一个“找分界点”的事情**。
模板
```cpp
int main(){
cin.tie(0) -> sync_with_stdio(0);
int l = 0, r = 210, mid, ans = 0;
while(l <= r){//[l,r]
mid = (l + r) >> 1;
if(check(mid)){
ans = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
cout << ans;
return 0;
}
```
---
##### 例1
我们需要处理接下来 $n$ 天的借教室信息,其中第 $i$ 天学校有 $r_i$ 个教室可供租借。共有 $m$ 份订单,每份订单用三个正整数描述,分别为 $d_j,s_j,t_j$,表示某租借者需要从第 $s_j$ 天到第 $t_j$ 天租借教室(包括第 $s_j$ 天和第 $t_j$ 天),每天需要租借 $d_j$ 个教室。
我们假定,租借者对教室的大小、地点没有要求。即对于每份订单,我们只需要每天提供 $d_j$ 个教室,而它们具体是哪些教室,每天是否是相同的教室则不用考虑。
借教室的原则是先到先得,也就是说我们要按照订单的先后顺序依次为每份订单分配教室。如果在分配的过程中遇到一份订单无法完全满足,则需要停止教室的分配,通知当前申请人修改订单。这里的无法满足指从第 $s_j$ 天到第 $t_j$ 天中有至少一天剩余的教室数量不足 $d_j$ 个。
现在我们需要知道,是否会有订单无法完全满足。如果有,需要通知哪一个申请人修改订单。
思路:
二分从哪个申请人开始会有订单无法满足。那么绿色部分代表的是“可以满足所有订单”,红色部分代表“不能满足所有订单”。我们要找红色部分的最左边那个哥们。
确定了 $1\sim mid$ 作为所有申请人之后,利用差分可以得到每天的教室需求。只需要判断需求量 $ sum $ 与 $ r[i] $ 的关系即可。
---
##### 例2
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度,计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
第一个问题要求我们计算最长不上升子序列的长度。
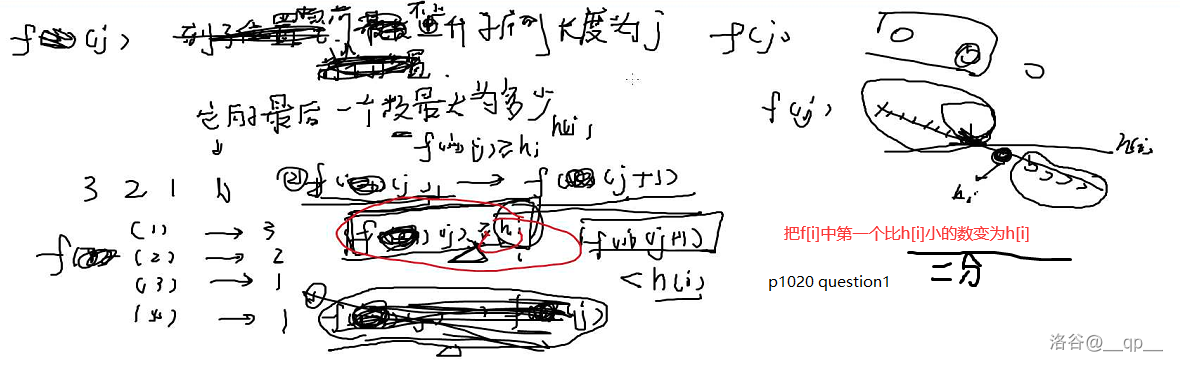
开一个f[j]数组,代表到第i个位置为止,长度为j的不上升子序列,最后一个位置最大是多少。
我们从1到n依次枚举i,考虑利用h[i]更新f[]数组,即我们希望找到一个以h[i]结尾的不上升子序列。
1. $f[] $ 数组本身应该是单调不上升的。
2. 如果 $ f[j] >= h[i] $,那么它们可以与 $ h[i] $ 拼成一个不上升子序列,结尾为 $ h[i] $,可以用来更新 $ f[j+1] $。
3. 如果 $ f[j] < h[i] $,那么它们不能与 $ h[i] $ 拼成一个不上升子序列。
4. 如果 $ f[j]>=h[i] $,那么它们没有必要被 $ h[i] $ 更新。
综上所述,我们需要找到第一个小于 $ h[i] $ 的 $ f[j] $,将它的值改为 $ h[i] $,二分即可。
对于第二问,我们考虑一个贪心。每次选取当前能覆盖它的导弹当中,高度最低的那个。如果没有这样的导弹,那么新开一个。
也就是我们要二分找到高度 $>=h[i]$ 的所有导弹中,高度最低的那个,同样可以二分。
发现这样求出来的结果与最长上升子序列的求法本质相同。
如图