P10814 【模板】离线二维数点
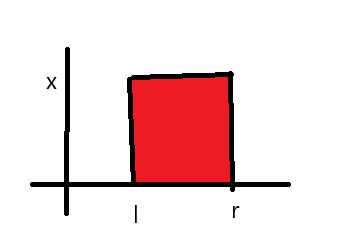
询问区间 \([l,r]\) 内,在值域为 \([0,x]\) 中数的个数。
想象这是个二维平面,我们要求的就是矩形内点的个数。
通常用 cdq 做,将询问拆成两个点,将点按照x坐标排序,按照y坐标加入到树状数组中(为了满足第二条限制),这时就依次加入点,并用树状数组进行前缀和相减,用两个前缀求区间信息,并且两个前缀都是在满足限制的情况下计算的。
P2163 [SHOI2007] 园丁的烦恼
同样二维数点题目,不过查询区间改为了矩形,我们同样用二维前缀和的做法,容斥掉多余的部分。
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define int ll
#define ls p<<1
#define rs p<<1|1
#define re register
#define pb push_back
#define pir pair<int,int>
#define f(a,x,i) for(int i=a;i<=x;i++)
#define fr(a,x,i) for(int i=a;i>=x;i--)
#define lb(x) x&(-x);
using namespace std;
const int N=5e5+10;
const int B=1e6+5;
const int M=8e6+10;
const int mod=1e9+7;int n,m;struct ss{int x,y,id,op,w;
}a[M];//点坐标struct sss{int x,y,z,h;
}q[N];int ans[N];//答案int cnt=1;int b[M],tot=0;//离散化
int len=0;int xx[N],yy[N];bool cmp(ss g,ss h){if(g.x!=h.x) return g.x<h.x;if(g.y!=h.y) return g.y<h.y;return g.w>h.w;
}int t[N+10];
void add(int x,int k){while(x<=len+10){t[x]+=k,x+=lb(x);}
}
int query(int x){int sum=0;while(x){sum+=t[x],x-=lb(x);}return sum;
}
void solve(){// freopen("a.in","r",stdin);// freopen("a.out","w",stdout); cin>>n>>m;for(int i=1;i<=n;i++){int x,y;cin>>x>>y;xx[i]=x;yy[i]=y;b[++tot]=x;b[++tot]=y;}for(int i=1;i<=m;i++){int x,y,z,h;cin>>x>>y>>z>>h;q[i]={x,y,z,h};b[++tot]=x;b[++tot]=y;b[++tot]=z;b[++tot]=h;}sort(b+1,b+1+tot);len=unique(b+1,b+1+tot)-b-1;for(int i=1;i<=n;i++){int x,y;x=lower_bound(b+1,b+1+len,xx[i])-b+2;y=lower_bound(b+1,b+1+len,yy[i])-b+2;a[cnt++]={x,y,0,1,1};}for(int i=1;i<=m;i++){int x,y,z,h;x=lower_bound(b+1,b+1+len,q[i].x)-b+2;y=lower_bound(b+1,b+1+len,q[i].y)-b+2;z=lower_bound(b+1,b+1+len,q[i].z)-b+2;h=lower_bound(b+1,b+1+len,q[i].h)-b+2;a[cnt++]={x-1,y-1,i,1,0};a[cnt++]={x-1,h,i,-1,0};a[cnt++]={z,y-1,i,-1,0};a[cnt++]={z,h,i,1,0};}cnt--;sort(a+1,a+cnt+1,cmp);for(int i=1;i<=cnt;i++){add(a[i].y,a[i].w);if(a[i].w==0){int sum=a[i].op*query(a[i].y);ans[a[i].id]+=sum; }}for(int i=1;i<=m;i++){cout<<ans[i]<<"\n";}
}
signed main(){ios::sync_with_stdio(0);cin.tie(nullptr);int t=1;// cin>>t;while(t--){solve();}return 0;
}








