算法学习笔记：扫描线-编程知识

算法学习笔记：扫描线

news/2025/1/30 13:13:05/文章来源:https://www.cnblogs.com/P2441M/p/18690820

前言

之前没什么理解，一做就废，最近集训讲了这个，感觉认识深刻了很多，遂写笔记。

这里讲的扫描线，更精确来说指的是离线二维数点，即用扫描线维护一维，DS 维护另一维。

概念

我们把二维数点放到平面上来，那么一个询问或限制就对应平面上的一个矩形，定义这个矩形的 $\text{side}$ 数为其被限制的边界数（不将坐标轴或上限的直线视为限制）。

裸题

Luogu P10814 【模板】离线二维数点

题意

给出长度为 $n$ 的序列 $a$，有 $m$ 次询问，每次询问给出 $l,r,x$，求出 $\sum_{i=l}^r[a_i\leq x]$。

对于所有数据，$1\leq n,m,a_i,l,r,x\leq 2\times 10^6$。

题解

模板题。以 $i$ 为一维，$a_i$ 为另一维建立平面。那么每次询问就是一个 $l\leq i\leq r \land a_i\leq x$ 的 $\text{3-side}$ 矩形。于是我们可以对 $a_i$ 维做扫描线，把 $(i,a_i)$ 的点挂到 $a_i$ 上，把 $(l,r,x)$ 的询问挂到 $x$ 上，每次扫到某个 $x$ 时取出所有挂在 $x$ 上的点 $(i,x)$，做单点加，然后回答所有挂在 $x$ 上的询问 $(l,r,x)$。需要支持单点加、区间查询，上 BIT 即可。时间复杂度 $O(n\log{n})$。

当然我们也可以对 $i$ 这一维做扫描线，换成权值 BIT 回答询问。这种写法貌似更常见。

实现 & 代码

讲讲实现。扫描线一般都有两种写法，一种是按要扫的维度排序，然后双指针移动；另一种是直接对要扫的维度的每一处都开一个 vector，每次更新信息或询问时，直接从对应的 vector 中取出相应的挂在当前位置的点或询问。前者常数优于后者。

这里给出第一种写法的实现：

#include <iostream>
#include <algorithm>
#include <vector>using namespace std;#define lowbit(x) ((x) & -(x))
#define chk_min(x, v) (x) = min((x), (v))
#define chk_max(x, v) (x) = max((x), (v))
typedef long long ll;
typedef pair<int, int> pii;
const int N = 2e6 + 5, M = 2e6 + 5, V = 2e6 + 5;namespace FastIO {const int S = 20 + 5;int szb;char buf[S];int read() {int s = 1; char ch = getchar();for (; ch < '0' || ch > '9'; ch = getchar())if (ch == '-') s = -1;int x = 0;for (; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + (ch ^ 48);return s * x;}void write(int x, char sep = '\n') {if (x < 0) putchar('-'), x = -x;do { buf[++szb] = x % 10 + '0', x /= 10; } while (x);while (szb) putchar(buf[szb--]);putchar(sep);}
}
using namespace FastIO;int n, m, sz, a[N], ans[M];
struct Query {int id, x, v, tp;bool operator<(const Query &q) const { return x < q.x; };
} q[M << 1];struct BIT {int c[V];int query(int x) {int s = 0;for (; x; x -= lowbit(x)) s += c[x];return s;}void add(int x, int v) { for (; x <= V - 5; x += lowbit(x)) c[x] += v; }
} ft;int main() {ios::sync_with_stdio(false); cin.tie(nullptr);n = read(), m = read();for (int i = 1; i <= n; ++i) a[i] = read();for (int i = 1; i <= m; ++i) {int l = read(), r = read(), v = read();if (l > 1) q[++sz] = { i, l - 1, v, -1 };q[++sz] = { i, r, v, 1 };}sort(q + 1, q + sz + 1);for (int i = 1, j = 1; i <= n; ++i) {ft.add(a[i], 1);while (j <= sz && q[j].x <= i) ans[q[j].id] += ft.query(q[j].v) * q[j].tp, ++j;}for (int i = 1; i <= m; ++i) write(ans[i]);return 0;
}

Luogu P1972 [SDOI2009] HH的项链

题意

给出长度为 $n$ 的序列 $a$，有 $m$ 次询问 $l,r$，求区间的颜色数，即区间内本质不同的数的个数。

对于所有数据，$1\leq n,m,a_i\leq 10^6$。

题解

典得不能再典的题。对于颜色数相关的问题，考虑预处理每个位置 $i$ 前面第一个与 $a_i$ 值相同的位置 $pre_i$，然后对于一个区间的询问，我们让所有第一次出现的位置产生贡献，那么总贡献就是颜色数，而区间内某个位置 $i$ 的数是第一次出现的充要条件就是 $pre_i<l$。于是以 $i$ 为一维，$pre_i$ 为另一维建立平面，那么每个询问就是查询一个 $\text{3-side}$ 矩形内的点数。和上一题一样有两种扫法，对 $pre_i$ 做扫描线，或者对 $i$ 做扫描线，并对 $pre_i$ 建立一个权值 BIT。时间复杂度依然是 $O(n\log{n})$ 的。

对询问建立平面

对于区间询问，分别以 $q_l$ 和 $q_r$ 为坐标轴建立平面也是一个很典的 trick。具体地，我们通常考虑怎样的询问 $(l,r)$ 对答案具有贡献，“有贡献”的限制在平面上表现为某类矩形，然后变成了平面上矩形加/覆盖之类的操作，查询则变成了单点查询。

CodeForces 522D Closest Equals

题意

给出长度为 $n$ 的序列 $a$，有 $m$ 次询问 $l,r$，求 $a[l,r]$ 中距离最近的相同元素。定义距离为下标之差的绝对值。

对于所有数据，$1\leq n,m\leq 5\times 10^5$。

题解

套路题。我们找出所有极近的相同元素的位置对 $(i,j)$，那么若 $l\leq i\land r\geq j$，则该位置对对询问区间有 $j-i$ 的 $\operatorname{chkmin}$ 贡献。问题转化成 $\text{2-side}$ 矩形 $\operatorname{chkmin}$ 和单点查询。随便对一维扫描线，我们当然可以 Segment Tree Beats 做。但是显然我们是前/后缀 $\operatorname{chkmin}$，对于这种特殊的最值操作，我们有更简单的实现方式：对于 $\operatorname{chkmin}$ 操作，我们做一种类似 tag 的方法，直接在单点上做最值修改，单点查询时查询后/前缀 $\min$ 就是答案。BIT 维护即可。时间复杂度 $O(n\log{n})$。

UOJ #637 【美团杯2021】A. 数据结构

题意

给出长度为 $n$ 的序列 $a$，有 $m$ 次询问 $l,r$，求出给 $a[l,r]$ 区间加 $1$ 后的全局颜色数。询问间相互独立。

对于所有数据，$1\leq a_i\leq n$，$1\leq n,m\leq 10^6$。

题解

挺有意思的题。正难则反，考虑对于每种颜色 $x$ 怎样的询问区间可 $(l,r) $以消去它的贡献。简单分析，显然需要同时满足以下条件：

所有的 $x$ 都被加 $1$；
所有的 $x-1$ 都没被加 $1$。

对于第 $1$ 个条件，我们预处理出 $x$ 第一次/最后一次出现的位置 $st_x/ed_x$，那么 $l\leq st_x \land r\geq ed_x$。对于第 $2$ 个条件，考虑 $x-1$ 所有极近的位置对 $i,j$，每个位置对都是一个限制 $l\geq i+1\land r\leq j-1$，对所有这样的限制取并集就是条件 $2$ 的限制。最终的限制就是两种限制的交集，放到平面上考虑，第 $1$ 种限制就是一个 $\text{2-side}$ 矩形，而第 $2$ 种限制则是一组点点相接的矩形。取交集就是在 $x-1$ 的出现位置的序列 $pos_{x-1}$ 中查找 $st_x$ 的前驱 $prv$ 和 $ed_x$ 的后继 $nxt$，然后得到 $prv+1\leq l\leq st_x\land ed_x\leq r\leq nxt-1$ 的 $\text{4-side}$ 矩形交。

问题转化为若干个 $\text{4-side}$ 矩形加（当然也有 $\text{2-side}$ 的，我们取限制最强的）和单点查询。这是很典的，对其中任意一维做扫描线，差分一下，让加的值在扫到入边时产生贡献，在扫完出边之后删除贡献，那就变成了序列上的区间加和单点查询，BIT 维护差分数组即可。

代码

需要一些讨论，所以放一下主要部分。代码比较古早时写的，所以写了 vector 的实现版本。

void addr(int lmn, int lmx, int rmn, int rmx) {ops[lmn].push_back({ rmn, rmx, 1 });ops[lmx + 1].push_back({ rmn, rmx, -1 });
}int main() {ios::sync_with_stdio(false); cin.tie(nullptr);cin >> n >> m;for (int i = 1; i <= n; ++i) cin >> a[i];for (int i = 1, l, r; i <= m; ++i) cin >> l >> r, qr[l].push_back({ i, r });for (int i = 1; i <= n; ++i) pos[a[i]].push_back(i);cnt = n + 1;for (int i = 1; i <= n + 1; ++i) {int lmn = 1, lmx = INF, rmn = -INF, rmx = n;if (pos[i].empty()) {if (!pos[i - 1].empty()) {addr(1, pos[i - 1].front() - 1, 1, pos[i - 1].front() - 1);addr(pos[i - 1].back() + 1, n, pos[i - 1].back() + 1, n);for (int j = 0; j < pos[i - 1].size() - 1; ++j) {int l = pos[i - 1][j], r = pos[i - 1][j + 1];addr(l + 1, r - 1, l + 1, r - 1);}} else --cnt;continue;}int st = pos[i].front(), ed = pos[i].back();int l = 1, r = n;bool suc = true;for (int &p : pos[i - 1]) {if (st <= p && p <= ed) { suc = false; break; }if (p < st) l = max(l, p + 1);if (p > ed) r = min(r, p - 1);}if (suc) addr(l, st, ed, r);}for (int i = 1; i <= n; ++i) {for (Op &op : ops[i]) {int l = op.l, r = op.r, v = op.v;ft.add(l, v); ft.add(r + 1, -v);}for (Query &q : qr[i]) ans[q.id] = ft.query(q.x);}for (int i = 1; i <= m; ++i) cout << cnt - ans[i] << '\n';return 0;
}

对区间右端点扫描线

另一种套路就是我们扫描线扫区间的右端点，然后用 DS 维护出所有左端点到当前右端点的答案。逆序扫区间左端点也是可以的。

QOJ #8672 排队

题意

给出 $n$ 个区间 $[l_i,r_i]$，定义 $f_i(x)=x+[x\in[l_i,r_i]]$。$q$ 次询问 $L,R$，求出 $f_R(f_{R-1}\cdots f_L(0)))$。

对于所有数据，$1\leq n,q\leq 10^6$。

题解

这不是我们的 ABC389F 吗？

我们对右端点做扫描线，然后维护所有 $a_L=f_R(f_{R-1}\cdots f_L(0)))$ 的值。考虑当 $R\leftarrow R+1$ 时 $a$ 怎么变化，显然若 $a_L\in[l_R,r_R]$，则 $a_L\leftarrow a_L+1$。而 $a_L$ 显然关于 $L$ 单调不增，因此我们可以将产生变化的位置是连续的，并且我们可以二分出来。于是需要支持区间加和单点查询，线段树上二分或树状数组上倍增都可以 $O(n\log{n})$ 的解决这题。不过这题不卡双 $\log$。

CodeForces 793F Julia the snail

题意

有一个长为 $n$ 的杆，上面有 $m$ 条绳子，每条绳子可以让蜗牛从 $l_i$ 爬到 $r_i$（中途不能离开）。蜗牛也可以自然下落。现在有 $q$ 次询问 $x,y$，你需要求出从高度 $x$ 出发，途中高度不能低于 $x$ 或高于 $y$，最高能爬到的高度。

对于所有数据，$1\leq n,m,q\leq 10^5$，保证 $r_i$ 互不相同。

题解

~~这破题也是 3000？？？~~
还是对右端点 $R$ 做扫描线，维护所有 $f_L$ 表示高度限制在 $[L,R]$ 内时能爬到的最大高度。当 $R\rightarrow R+1$ 时，考虑以 $R$ 为右端的绳子 $[L',R]$，那么我们对于所有 $f_L\geq L'$，显然可以让蜗牛从 $f_L$ 自然滑落到 $L'$，然后爬到 $R$，所以此时令 $f_L\leftarrow R$。我们上 Segment Tree Beats 就 $O(n\log{n})$ 地做完了。

CodeForces 1083D The Fair Nut's getting crazy

题意

给出长度为 $n$ 的序列 $a$。你需要从该序列中选出两个非空的子段，这两个子段满足：

两个子段非包含关系；
两个子段存在交且位于两个子段交中的元素在每个子段中只能出现一次。

求共有多少种不同的子段选择方案。输出总方案数对 $10^9 + 7$ 取模后的结果。

选择子段 $[a, b],[c, d]$ 与选择子段 $[c, d],[a, b]$ 被视为是相同的两种方案。

对于所有数据，$1\leq n\leq 10^5, -10^9\leq a_i\leq 10^9$。

题解

设 $a<c\leq b<d$。一个很 naive 的想法就是枚举交集区间 $[c,b]$，预处理每个位置 $i$ 前面/后面第一个与 $a_i$ 值相同的位置 $pre_i/nxt_i$，我们有 $a\geq\max_{i=c}^b\{pre_i\}+1$ 和 $d\leq \min_{i=c}^b\{nxt_i\}-1$，所以此时能选出的子段方案数即为 $((c-1)-mx)(mn-(b+1))$。

扫描线优化一下。我们对 $R$ 做扫描线，然后对每个 $L$ 维护交集区间为 $[L,R]$ 时的子段方案数，然后用线段树维护区间和累计到答案上。我们需要维护

\[\begin{align*} &\sum ((L-1)-mx)(mn-(R+1)) \\ =&\sum (L-1)mn-(L-1)(R+1)-mx\times mn+(R+1)mx \\ =&\sum (L-1)mn-(R+1)\sum(L-1)-\sum mx\times mn+(R+1)\sum mx \end{align*} \]

所以我们需要在线段树的每个节点上维护 $\sum (L-1)mn,\sum mx,\sum mn,\sum mx\times mn$。

$R\leftarrow R+1$ 后 $mn$ 和 $mx$ 会对应发生变化，对于这类变化有经典的套路：注意到我们需要维护后缀最值，考虑单调栈，以 $mx$ 为例，当我们加入一个数 $a_R$ 时，$mx$ 是成段变化的，具体来说，我们维护一个栈内元素单调递减的单调栈，设栈顶为 $top$，那么实际上它蕴含了一个后缀最值信息

\[\max_{i=stk_{top-1}+1}^{stk_{top}}=a_{stk_{top}} \]

当 $a_{stk_{top}}\leq a_R$ 时，我们弹出栈顶，同时更新这一段的 $mx\leftarrow a_R$，这样就可以正确地维护好 $mx$ 了，$mn$ 同理。我们只在弹出栈顶时进行 $1$ 次区间覆盖，因此区间覆盖的总次数为 $O(n)$。

扫描线的过程中还要双指针求出最长的不存在相同元素的交集区间，然后线段树和单调栈相配合就做完了。时间复杂度 $O(n\log{n})$。

代码

代码不是很好写，所以放一下主要部分。

struct SegTree {
#define ls(p) (p << 1)
#define rs(p) (p << 1 | 1)struct Node { ll sum[4], tg[2]; } nodes[(N << 2) + 5];void push_up(int p) {for (int i = 0; i < 4; ++i)nodes[p].sum[i] = (nodes[ls(p)].sum[i] + nodes[rs(p)].sum[i]) % MOD;}void make_change(int p, int l, int r, ll v, int tp) {nodes[p].sum[2] = nodes[p].sum[tp ^ 1] * v % MOD;nodes[p].sum[tp] = v * (r - l + 1) % MOD;if (!tp) nodes[p].sum[3] = v * (1ll * (l + r) * (r - l + 1) / 2 % MOD) % MOD;nodes[p].tg[tp] = v;}void push_down(int p, int l, int r) {int mid = (l + r) >> 1;for (int i = 0; i <= 1; ++i) {if (!nodes[p].tg[i]) continue;make_change(ls(p), l, mid, nodes[p].tg[i], i),make_change(rs(p), mid + 1, r, nodes[p].tg[i], i);nodes[p].tg[i] = 0;}}ll query(int p, int l, int r, int x, int y, int tp) {if (x <= l && y >= r) return nodes[p].sum[tp];push_down(p, l, r);int mid = (l + r) >> 1;ll res = 0;if (x <= mid) res = query(ls(p), l, mid, x, y, tp);if (y > mid) res = (res + query(rs(p), mid + 1, r, x, y, tp)) % MOD;return res;}void change(int p, int l, int r, int x, int y, ll v, int tp) {if (x <= l && y >= r) { make_change(p, l, r, v, tp); return; }push_down(p, l, r);int mid = (l + r) >> 1;if (x <= mid) change(ls(p), l, mid, x, y, v, tp);if (y > mid) change(rs(p), mid + 1, r, x, y, v, tp);push_up(p);}
#undef ls
#undef rs
} sgt;int main() {ios::sync_with_stdio(false); cin.tie(nullptr);cin >> n;for (int i = 1; i <= n; ++i) cin >> a[i], da[++sz] = a[i];sort(da + 1, da + sz + 1); sz = unique(da + 1, da + sz + 1) - (da + 1);for (int i = 1; i <= n; ++i) {a[i] = lower_bound(da + 1, da + sz + 1, a[i]) - da;pre[i] = pos[a[i]] + 1; pos[a[i]] = i;}for (int i = 1; i <= sz; ++i) pos[i] = n + 1;for (int i = n; i; --i) nxt[i] = pos[a[i]] - 1, pos[a[i]] = i;for (int i = n; i; --i) {while (top && pre[stk[top]] < pre[i]) --top; fp[i] = top ? stk[top] : n + 1; stk[++top] = i; }top = 0; for (int i = n; i; --i) {while (top && nxt[stk[top]] > nxt[i]) --top; fn[i] = top ? stk[top] : n + 1; stk[++top] = i; }for (int l = n, r = n; l; --l) {if (l < fp[l]) sgt.change(1, 1, n, l, fp[l] - 1, pre[l], 0);if (l < fn[l]) sgt.change(1, 1, n, l, fn[l] - 1, nxt[l], 1); ++cnt[a[l]];while (cnt[a[l]] > 1) --cnt[a[r--]];ans = (ans + sgt.query(1, 1, n, l, r, 1) * l % MOD) % MOD; ans = (ans + sgt.query(1, 1, n, l, r, 3)) % MOD; ans = (ans - sgt.query(1, 1, n, l, r, 2)) % MOD; ans = (ans - 1ll * l * (1ll * (l + r) * (r - l + 1) / 2 % MOD)) % MOD; }cout << (ans + MOD) % MOD;return 0;
}

区间子区间问题

还有一类问题，多次询问一个区间，让我们求出这区间内所有子区间的贡献的累计值。

首先你要会我们唐唐的【模板】线段树 3，也就是区间历史最值/版本和。我们还是考虑对 $R$ 做扫描线，此时对于一个询问 $[L,R]$，若我们查询 $[L,R]$ 的区间和，得到的是区间中所有以 $R$ 为右端点的子区间的贡献之和。但如果我们查询 $[L,R]$ 的区间历史版本和呢？其实就是询问区间内所有子区间的贡献之和了。

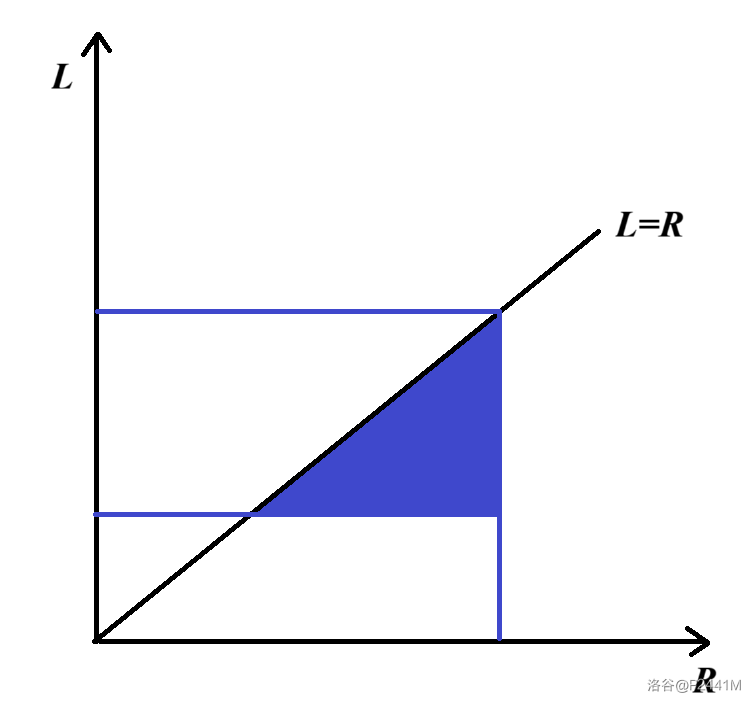
如上图所示，我们要求的是蓝色区域内的贡献之和，而查询区间历史版本和实际上查询的是蓝色边界内的 $\text{3-side}$ 矩形内的贡献和，但这依然是正确的，注意我们有 $L\leq R$，也就是所有区间表示的点都落在直线 $L=R$ 下方，所以我们多查询的那个部分内没有合法区间。

Luogu P3246 [HNOI2016] 序列

题意

给出长度为 $n$ 的序列 $a$，$q$ 次询问 $l,r$，求出 $a[l,r]$ 内所有子区间的最小值之和。

对于所有数据，$1\leq n,q\leq 10^5$。

题解

奶龙题。对 $r$ 做扫描线，用前面的单调栈的套路维护出所有的 $\min_{i=l}^r\{a_i\}$。那么就是一个简单的区间加和区间历史版本和了。时间复杂度 $O(n\log{n})$。

CodeForces 997E Good Subsegments

题意

给出长度为 $n$ 的排列 $p$。定义一个区间 $[l,r]$ 是好的当且仅当 $p[l,r]$ 在值域上是连续的。$q$ 次询问 $l,r$，求出 $a[l,r]$ 中有多少个子区间是好的。

对于所有数据，$1\leq n,q\leq 1.2\times 10^5$。

题解

因为是排列，所以一个区间是好的等价于 $mx-mn+1=r-l+1$，所以我们在扫描线的过程中维护 $mx-mn+l$，然后观察到 $mx-mn+l\ge r$，因此我们记录最小值和出现次数，并且维护出现次数的历史版本和即可。时间复杂度 $O(n\log{n})$。

代码

主要放线段树的部分。

双倍经验

struct SegTree {
#define ls(p) (p << 1)
#define rs(p) (p << 1 | 1)struct Node { ll mn, cmn, hcmn, tg_add, tg_cnt; } nodes[N << 2];void push_up(int p) {nodes[p].mn = min(nodes[ls(p)].mn, nodes[rs(p)].mn);nodes[p].cmn = 0;if (nodes[ls(p)].mn == nodes[p].mn) nodes[p].cmn += nodes[ls(p)].cmn;if (nodes[rs(p)].mn == nodes[p].mn) nodes[p].cmn += nodes[rs(p)].cmn;}void make_add(int p, ll add, ll cnt) {nodes[p].mn += add; nodes[p].tg_add += add;nodes[p].tg_cnt += cnt; nodes[p].hcmn += cnt * nodes[p].cmn;}void push_down(int p) {ll &add = nodes[p].tg_add, &cnt = nodes[p].tg_cnt;ll mn = min(nodes[ls(p)].mn, nodes[rs(p)].mn);make_add(ls(p), add, nodes[ls(p)].mn == mn ? cnt : 0);make_add(rs(p), add, nodes[rs(p)].mn == mn ? cnt : 0);add = cnt = 0;}void build(int p, int l, int r) {nodes[p].tg_add = nodes[p].tg_cnt = 0;nodes[p].mn = l; nodes[p].cmn = 1;if (l == r) return;int mid = (l + r) >> 1;build(ls(p), l, mid); build(rs(p), mid + 1, r);push_up(p);}void add(int p, int l, int r, int x, int y, ll v) {if (x <= l && y >= r) { make_add(p, v, 0); return; }push_down(p);int mid = (l + r) >> 1;if (x <= mid) add(ls(p), l, mid, x, y, v);if (y > mid) add(rs(p), mid + 1, r, x, y, v);push_up(p);}ll query(int p, int l, int r, int x, int y) {if (x <= l && y >= r) return nodes[p].hcmn;push_down(p);int mid = (l + r) >> 1; ll res = 0;if (x <= mid) res = query(ls(p), l, mid, x, y);if (y > mid) res += query(rs(p), mid + 1, r, x, y);return res;}
#undef ls
#undef rs
} sgt;

Luogu P10822 [EC Final 2020] Prof. Pang's sequence

题意

给出长度为 $n$ 的序列 $a$，$m$ 次询问 $l,r$，求出 $a[l,r]$ 中有多少个子区间的颜色数为奇数。

对于所有数据，$1\leq n,m\leq 5\times 10^5$。

题解

注意到子区间的颜色数为奇数的个数等价于所有子区间的颜色数 $\bmod 2$ 的和。扫描线维护子区间颜色数 $\bmod 2$，相当于维护一个 $0/1$ 序列，考虑 $R\leftarrow R+1$ 时，$[pre_R+1,R]$ 的颜色数都会 $+1$，表现在 $0/1$ 序列上就是区间反转。所以我们需要支持区间反转和历史版本和，对打/没打 $rev$ 的 tag 的状态分别记录历史版本和的更新标记的个数即可。时间复杂度 $O(n\log{n})$。

代码

还是放线段树代码。

struct SegTree {
#define ls(p) (p << 1)
#define rs(p) (p << 1 | 1)struct Node { ll sum, hsum, cnt0, cnt1, tg; } nodes[N << 2];void push_up(int p) {nodes[p].sum = nodes[ls(p)].sum + nodes[rs(p)].sum;nodes[p].hsum = nodes[ls(p)].hsum + nodes[rs(p)].hsum;}void make_tg(int p, int l, int r, int cnt0, int cnt1, int tg) {nodes[p].hsum += nodes[p].sum * cnt0 + (r - l + 1 - nodes[p].sum) * cnt1;if (nodes[p].tg) nodes[p].cnt0 += cnt1, nodes[p].cnt1 += cnt0;else nodes[p].cnt0 += cnt0, nodes[p].cnt1 += cnt1;if (tg) nodes[p].tg ^= 1, nodes[p].sum = r - l + 1 - nodes[p].sum;}void push_down(int p, int l, int r) {int mid = (l + r) >> 1;make_tg(ls(p), l, mid, nodes[p].cnt0, nodes[p].cnt1, nodes[p].tg);make_tg(rs(p), mid + 1, r, nodes[p].cnt0, nodes[p].cnt1, nodes[p].tg);nodes[p].cnt0 = nodes[p].cnt1 = nodes[p].tg = 0;}void build(int p, int l, int r) {if (l == r) return;int mid = (l + r) >> 1;build(ls(p), l, mid); build(rs(p), mid + 1, r);push_up(p);}ll query(int p, int l, int r, int x, int y) {if (x <= l && y >= r) return nodes[p].hsum;push_down(p, l, r);int mid = (l + r) >> 1; ll res = 0;if (x <= mid) res = query(ls(p), l, mid, x, y);if (y > mid) res += query(rs(p), mid + 1, r, x, y);return res;}void rev(int p, int l, int r, int x, int y) {if (x <= l && y >= r) { make_tg(p, l, r, 0, 0, 1); return; }push_down(p, l, r);int mid = (l + r) >> 1;if (x <= mid) rev(ls(p), l, mid, x, y);if (y > mid) rev(rs(p), mid + 1, r, x, y);push_up(p);}
#undef ls
#undef rs
} sgt;

换维扫描线

对于很常规的 DS 问题，我们通常的做法就是沿时间顺序进行操作。考虑以序列一维，时间一维建立平面，那么我们这么做等价于对时间维做扫描线。而对于一些更复杂的操作，有时这么做略显吃力，那么我们能不能对序列维做扫描线呢？答案是可以的。这种做法就被叫做换维扫描线。面对一些单点查询和修改操作可差分的情形下，可以考虑换维扫描线。

Luogu P7560 [JOISC 2021 Day1] フードコート

题意

有 $n$ 个队列。给出值域 $m$，进行 $q$ 次操作，操作有以下三种：

向编号在 $[l,r]$ 中的队列的尾部加入 $k$ 个 $c$；
把编号在 $[l,r]$ 中的队列的前 $k$ 个数删去，若队列大小不足 $k$ 则清空队列；
查询编号为 $a$ 的队列中从队头开始的第 $b$ 个数，若队列大小不足 $b$ 则返回 $0$。

对于所有数据，$1\leq c\leq m$，$1\leq n,m,q\leq 2.5\times 10^5$。

题解

发现这个操作看上去很难维护的样子，但是是经典的单点查询和可差分修改，所以考虑换维扫描线，在这题中，我们对队列的编号做扫描线，用 DS 维护时间轴上的信息。然后对操作 $1,2$ 差分一下，让它在 $L$ 处产生 $k$ 的贡献，在 $R+1$ 处删除贡献。

先考虑没有操作 $2$ 怎么做，显然直接在时间轴上把最小的前缀和 $\ge b$ 的位置二分出来，对应的插入的数就是答案。那有操作 $2$ 之后，这个方法为什么不能沿用呢？因为删除操作破坏了前缀和的单调性使得我们不能二分求出答案。

我们再尝试弱化一下，发现这个清空使得我们要对 $0$ 取 $\max$，有点烦，考虑前缀和始终 $\ge 0$ 怎么做。容易观察到，此时我们把删除操作全部延后不影响正确性，那么我们记录当前询问操作之前操作 $2$ 的贡献和 $\sum{del}$，然后在只考虑操作 $1$ 的操作序列上把前缀和 $\ge b+\sum{del}$ 的最小位置二分出来就是答案。

最后回到前缀和可能触底 $<0$ 的情况，这时考虑当前询问前的最后一次触底的时刻，在这个时刻之后，我们套用上面的做法就是正确的！

key observation：最后一次触底的时刻就是前缀和最小的时刻。

证明：注意到在时刻 $i$ 触底之后再一次在时刻 $j$ 触底等价于 $sum_j-sum_i<0$，显然得证。

想想我们现在需要支持什么操作。首先需要支持查询 $[1,b)$ 的前缀和最小值，而修改操作已经被换维扫描线转化成了单点加操作，因此维护前缀和序列，查询时查询 $[1,b)$ 的前缀最小值，单点加转化为后缀加即可。找到前缀最小值的位置 $p$ 后，我们需要在只考虑操作 $1$ 的操作序列的 $(p,t]$ 子区间上，二分出前缀和 $\ge b+\sum{del}$ 的最小位置，其中 $t$ 为当前询问的时间。我们用线段树维护贡献和 $\sum{sum}$ 和只考虑操作 $1$ 的贡献和 $\sum{add}$，此时 $\sum{del}=\sum{add}-\sum{sum}$，询问时做线段树二分即可。

所以开两颗线段树就能维护出所有需要的信息。时间复杂度 $O(q\log{q})$。

代码

实现时注意一些特判。我把两颗线段树合并在一起了。

双倍经验

#include <iostream>
#include <algorithm>using namespace std;#define lowbit(x) ((x) & -(x))
#define chk_min(x, v) (x) = min((x), (v))
#define chk_max(x, v) (x) = max((x), (v))
typedef long long ll;
typedef pair<int, int> pii;
const int Q = 5e5 + 5;int n, m, q, num[Q];
ll ans[Q];
int cnt_qr, cnt_ops;
struct Query {ll num, id, a, b;bool operator<(const Query &x) const { return a < x.a; }
} qr[Q];
struct Op {ll id, tp, a, k;bool operator<(const Op &x) const { return a < x.a; }
} ops[Q];struct SegTree {
#define ls(p) (p << 1)
#define rs(p) (p << 1 | 1)struct Node { ll sum, add_sum, mn, amn, tg; } nodes[Q << 2];void push_up(Node &p, Node &lp, Node &rp) {p.sum = lp.sum + rp.sum; p.add_sum = lp.add_sum + rp.add_sum;p.mn = min(lp.mn, rp.mn);p.amn = rp.mn <= lp.mn ? rp.amn : lp.amn;}void push_up(int p) { push_up(nodes[p], nodes[ls(p)], nodes[rs(p)]); }void make_add(int p, int l, int r, ll v) { nodes[p].tg += v; nodes[p].mn += v; }void push_down(int p, int l, int r) {if (!nodes[p].tg) return;int mid = (l + r) >> 1;make_add(ls(p), l, mid, nodes[p].tg); make_add(rs(p), mid + 1, r, nodes[p].tg);nodes[p].tg = 0;}void build(int p, int l, int r) {if (l == r) { nodes[p].amn = l; return; }int mid = (l + r) >> 1;build(ls(p), l, mid); build(rs(p), mid + 1, r);push_up(p);}Node query(int p, int l, int r, int x, int y) {if (x <= l && y >= r) return nodes[p];push_down(p, l, r);int mid = (l + r) >> 1;if (x <= mid && y > mid) {Node lres = query(ls(p), l, mid, x, y);Node rres = query(rs(p), mid + 1, r, x, y), res;return push_up(res, lres, rres), res;}return x <= mid ? query(ls(p), l, mid, x, y) : query(rs(p), mid + 1, r, x, y);}int find(int p, int l, int r, int x, ll &v) {if (r < x) return 0;push_down(p, l, r);if (x <= l) {if (nodes[p].add_sum < v) { v -= nodes[p].add_sum; return 0; }if (l == r) return l;}int mid = (l + r) >> 1;int res = find(ls(p), l, mid, x, v);return res ? res : find(rs(p), mid + 1, r, x, v);}void add(int p, int l, int r, int x, int y, ll v) {if (x <= l && y >= r) { make_add(p, l, r, v); return; }push_down(p, l, r);int mid = (l + r) >> 1;if (x <= mid) add(ls(p), l, mid, x, y, v);if (y > mid) add(rs(p), mid + 1, r, x, y, v);push_up(p);}void add2(int p, int l, int r, int x, ll v, int tp) {if (l == r) {nodes[p].sum += v;if (tp) nodes[p].add_sum += v;return;}push_down(p, l, r);int mid = (l + r) >> 1;if (x <= mid) add2(ls(p), l, mid, x, v, tp);else add2(rs(p), mid + 1, r, x, v, tp);push_up(p);}
#undef ls
#undef rs
} sgt;
using Node = SegTree::Node;int main() {ios::sync_with_stdio(false); cin.tie(nullptr);cin >> n >> m >> q;for (int i = 1, tp; i <= q; ++i) {cin >> tp;if (tp == 1) {ll l, r, k; cin >> l >> r >> num[i] >> k;ops[++cnt_ops] = { i, 1, l, k }; ops[++cnt_ops] = { i, 1, r + 1, -k };} else if (tp == 2) {ll l, r, k; cin >> l >> r >> k;ops[++cnt_ops] = { i, 0, l, -k }; ops[++cnt_ops] = { i, 0, r + 1, k };} else {ll a, b; cin >> a >> b; ++cnt_qr;qr[cnt_qr] = { cnt_qr, i, a, b };}ans[i] = m + 1;}sort(ops + 1, ops + cnt_ops + 1); sort(qr + 1, qr + cnt_qr + 1);sgt.build(1, 1, q);for (int i = 1, j = 1, k = 1; i <= n; ++i) {while (j <= cnt_ops && ops[j].a == i)sgt.add(1, 1, q, ops[j].id, q, ops[j].k), sgt.add2(1, 1, q, ops[j].id, ops[j].k, ops[j].tp), ++j;while (k <= cnt_qr && qr[k].a == i) {if (qr[k].id == 1) { ans[qr[k++].num] = 0; continue; }Node res = sgt.query(1, 1, q, 1, qr[k].id - 1);int p = res.mn >= 0 ? 0 : res.amn;Node res2 = sgt.query(1, 1, q, p + 1, qr[k].id);ll del = res2.add_sum - res2.sum, val = qr[k].b + del;int pos = sgt.find(1, 1, q, p + 1, val);ans[qr[k].num] = (!pos || pos > qr[k].id) ? 0 : num[pos];++k;}}for (int i = 1; i <= cnt_qr; ++i) cout << ans[i] << '\n';return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/876104.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！