Cow Checkups 题解
题目大意:
对于每一个 \(c=0…n\),求出区间 \([l, r]\) 能使得翻转此区间后满足 \(\sum_{i=1}^n (a_i = b_i)\) 的值恰好为 \(c\) 的数量。
解法:
首先,我们定义两个二维数组:
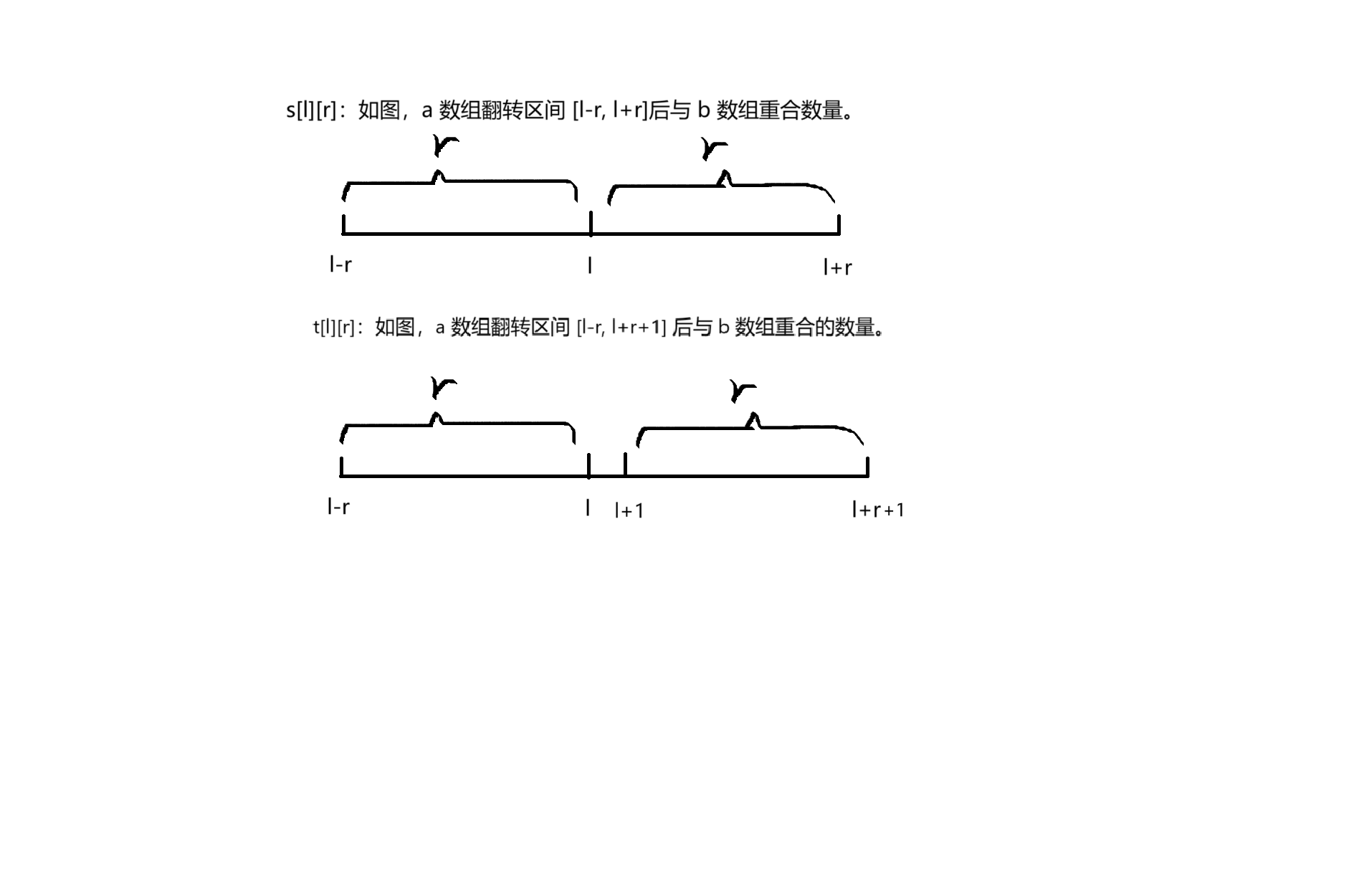
- \(s_{l, r}\) : 以 \(l\) 为中点 左右长度为 \(r\),即区间 \([l - r, l + r]\) 翻转后的重合数量
- \(t_{l, r}\) : 以 \(l, l + 1\) 为中点 左右长度为 \(r\),即区间 \([l - r, l + r + 1]\) 翻转后的重合数量
这样方便处理每个奇、偶数长度的区间。
为了方便大家理解这两个数组,我来用样例讲解一下。
\(input:\)
7
1 3 2 2 1 3 2
3 2 2 1 2 3 1
第一,\(s_{3, 2}\) 等于?
根据定义,翻转区间 \([3-2,3+2] = [1,5]\) 后 \(a\) 数组成为了:\(\textcolor{red}{1,2,2,3,1},3,2\)。
与 \(b\) 数组重合的位置有 \(2,3\),故 \(s_{3,2} = 2\)。
第二,\(t_{4,1}\) 等于?
根据定义,翻转区间 \([4-1,4+1+1] = [3,6]\) 后 \(a\) 数组成为了:\(1,3,\textcolor{red}{3,1,2,2},2\)。
与 \(b\) 数组重合的位置有 \(4,5\),故 \(t_{4,1} = 2\)。
数据范围是 \(n \le 7500\),那么我们求这两个数组的时间复杂度只能控制在 \(\mathcal{O}(n^2)\)。
由此,一个优秀的算法浮现在了我们的脑海中。
首先,初始化:
\(s_{i,0} = (a_i == b_i)\)
\(t_{i,0} = (a_i == b_{i+1}) + (a_{i + 1} == b_i)\)
so easy,就不多说了。
然后,怎么转移?
其实也不难。
\(s_{i,j} = s_{i,j-1} + (a_{i-j} == b_{i+j}) + (a_{i+j} == b_{i-j})\)
相当于 \(s_{i,j}\) 在 \(s_{i,j-1}\) 的基础上左右各增加了一个数,只需再算左右两数翻转后是否满足 \(a_i == b_i\) 即可。
\(t_{i,j}\) 也同理。
\(t_{i,j} = t_{i,j-1} + (a_{i + j + 1} == b_{i - j}) + (a_{i - j} == b_{i + j + 1})\)
最后,就可以统计答案了。
对 \(a_i==b_i\) 做一个前缀和。
枚举要翻转的区间 \([l,r]\),用 \(s\) 与 \(t\) 数组去计算翻转后的值。
而区间 \([1,l-1]\) 与 \([r+1,n]\) 则用前缀和计算即可。
讲一下怎么实现:
求出区间中点 \(mid = (l+r+1) \div 2\)。
若区间长度为奇数,答案就是 \(s_{mid, mid-l}\)
若区间长度为偶数,答案就是 \(t_{mid, mid-l}\)
自己想一想,建议画图去理解一下。其实并不难。
Code:
由上面的分析,敲出了以下代码:
#include <bits/stdc++.h>
#define ll long long
#define pii pair <int, int>
using namespace std;
const int N = 7.5e3 + 10;
int a[N], b[N]; ll s[N][N], t[N][N], pre[N], ans[N];
// s[l][r] : 以 l 为中点 左右长度为 r reverse 后的重合数量
// t[l][r] : 以 l, l + 1 为中点 左右长度为 r reverse 后的重合数量
signed main() {ios::sync_with_stdio(false);cin.tie(nullptr); cout.tie(nullptr);int n; cin >> n;for (int i = 1; i <= n; ++i)cin >> a[i];for (int i = 1; i <= n; ++i)cin >> b[i];for (int i = 1; i <= n; ++i) {s[i][0] = (a[i] == b[i]);for (int j = 1; j <= min(i - 1, n - i); ++j)s[i][j] = s[i][j - 1] + (a[i + j] == b[i - j]) + (a[i - j] == b[i + j]);}for (int i = 1; i < n; ++i) {t[i][0] = (a[i] == b[i + 1]) + (a[i + 1] == b[i]);for (int j = 1; j <= min(i - 1, n - i - 1); ++j)t[i][j] = t[i][j - 1] + (a[i + j + 1] == b[i - j]) + (a[i - j] == b[i + j + 1]);}for (int i = 1; i <= n; ++i)pre[i] = pre[i - 1] + (a[i] == b[i]);for (int l = 1; l <= n; ++l) {for (int r = l; r <= n; ++r) {int mid = (l + r) / 2;int ret = 0;if ((r - l + 1) & 1) {ret = (s[mid][mid - l]) + pre[l - 1] + pre[n] - pre[r];} else {ret = (t[mid][mid - l]) + pre[l - 1] + pre[n] - pre[r];}ans[ret] ++;}}for (int i = 0; i <= n; ++i)cout << ans[i] << "\n";return 0;
}
样例本地全过,交上去就 \(MLE\) 了,一分没有。
怎么办?难道要前功尽弃吗?不,先卡卡常。
不必要的 \(long\ long\) 去掉。\(s\),\(t\) 数组可以只留一个(即先求长度为奇数的区间,再求偶数区间)。
又写出以下代码:
#include <bits/stdc++.h>
#define ll long long
#define pii pair <int, int>
using namespace std;
const int N = 7.5e3 + 10;
int a[N], b[N];
int s[N][N], pre[N], ans[N];
// s[l][r] : 以 l 为中点 左右长度为 r reverse 后的重合数量
// s2[l][r] : 以 l, l + 1 为中点 左右长度为 r reverse 后的重合数量
signed main() {ios::sync_with_stdio(false);cin.tie(nullptr); cout.tie(nullptr);int n; cin >> n;for (int i = 1; i <= n; ++i)cin >> a[i];for (int i = 1; i <= n; ++i)cin >> b[i];for (int i = 1; i <= n; ++i) {s[i][0] = (a[i] == b[i]);for (int j = 1; j <= min(i - 1, n - i); ++j)s[i][j] = s[i][j - 1] + (a[i + j] == b[i - j]) + (a[i - j] == b[i + j]);}for (int i = 1; i <= n; ++i)pre[i] = pre[i - 1] + (a[i] == b[i]);for (int l = 1; l <= n; ++l) {for (int r = l; r <= n; ++r) {int mid = (l + r) / 2;int ret = 0;if ((r - l + 1) & 1) {ret = (s[mid][mid - l]) + pre[l - 1] + pre[n] - pre[r];ans[ret] ++;} else ;}}for (int i = 1; i < n; ++i) {s[i][0] = (a[i] == b[i + 1]) + (a[i + 1] == b[i]);for (int j = 1; j <= min(i - 1, n - i - 1); ++j)s[i][j] = s[i][j - 1] + (a[i + j + 1] == b[i - j]) + (a[i - j] == b[i + j + 1]);}for (int l = 1; l <= n; ++l) {for (int r = l; r <= n; ++r) {int mid = (l + r) / 2;int ret = 0;if ((r - l + 1) & 1) ;else {ret = (s[mid][mid - l]) + pre[l - 1] + pre[n] - pre[r];ans[ret] ++;}}}for (int i = 0; i <= n; ++i)cout << ans[i] << "\n";return 0;
}
不出所料,通过了。
总结:
这是一道很好的铜组题目,我的这种方法稍微需要动脑,不知道是否有更简单的做法。
另外,这题也是新手练题的极佳选择。Good!









