简单图论与构造
A
考虑把权值为 2 的点看作给权值为 1 的点加一,
所以整个问题被拆成了两个部分:构造树和给节点加一
事实上,在第一部分时我们将树构造的尽量平衡是有好处,这个结论在第二个步骤中会得到证明
构造:
Process DFS(father,ch,u,size):if size==0 then returnson[father][ch]=usize=size-1DFS(u,0,v,size/2)DFS(u,1,v',size-size/2)然后考虑分配加一的点数,具体的需要注意到:
给一个节点加一对子树内的平衡性是不产生影响的
所以考虑从上往下贪心的分配,每次给自己加一后优先给小的子树分配一个
然后再对半分,而由于树是尽量平衡的,所以每个节点和自己的兄弟的差至多是一,是满足这个贪心的分配结构的
B
递归构造,假如某个节点的所有的子树都已经构造出了答案,
对于每个儿子 \(v\) 的答案为 \(array[v]=\{v_{state_1},v_{state_2},v_{state_3} ...\}\) ,那么考虑多元组:
经历如下过程:
i: 1 -> xthen j: 1 -> 2i: x -> 1then j: 2 -> 3
...then j: y-1 -> ythen k: 1 -> 2
i: 1 -> xthen j: y -> y-1...
即可
C
转化一下题意,把每次给出来的二元组看成边,那么就是要给边配对,使得配对的两条边是共用顶点的
那么我们先考虑联通图的情形,
如果是一棵树,我们考虑归纳构造:
在以 \(u\) 为根的子树内的边相互匹配,那么如果子树里有偶数个边,那么一定存在一种恰好匹配完的方式
如果有奇数个边,那么一定有一种是使得剩下的那个边是 \(u\) 连向自己的父亲的,然后放到父亲那里继续匹配(\(u\) 的兄弟节点之间匹配)
图的情况是一致的,因为在 DFS 生成树上,非树边一定是反祖边,一起放到父亲那里考虑即可
D
对于前 \(n\over 2\) 份作业,我们钦定他们谁都不能打爆谁,对于后 \(n\over 2\) 份作业,我们钦定靠前的一定能打爆靠后的,容易发现,这样的能够构造出
次的比对,符合要求
E
简单等积变形即可
首先可以知道 \(k | n \times m \times 2\) ,然后设 \(x=\frac{n \times m \times 2} k\) 。
假如 \(n \ge x\) ,那么直接令底为 \(x\) ,令高为 \(1\)。
假如 \(n < x\) ,那么令底为 \(n\) ,然后就可以得知高为 \(\frac x n\) ,但是这个可能是一个小数,因此就需要用等积变形把它变成一个整数的坐标。现在三角形的底是平行于坐标轴的,如下:
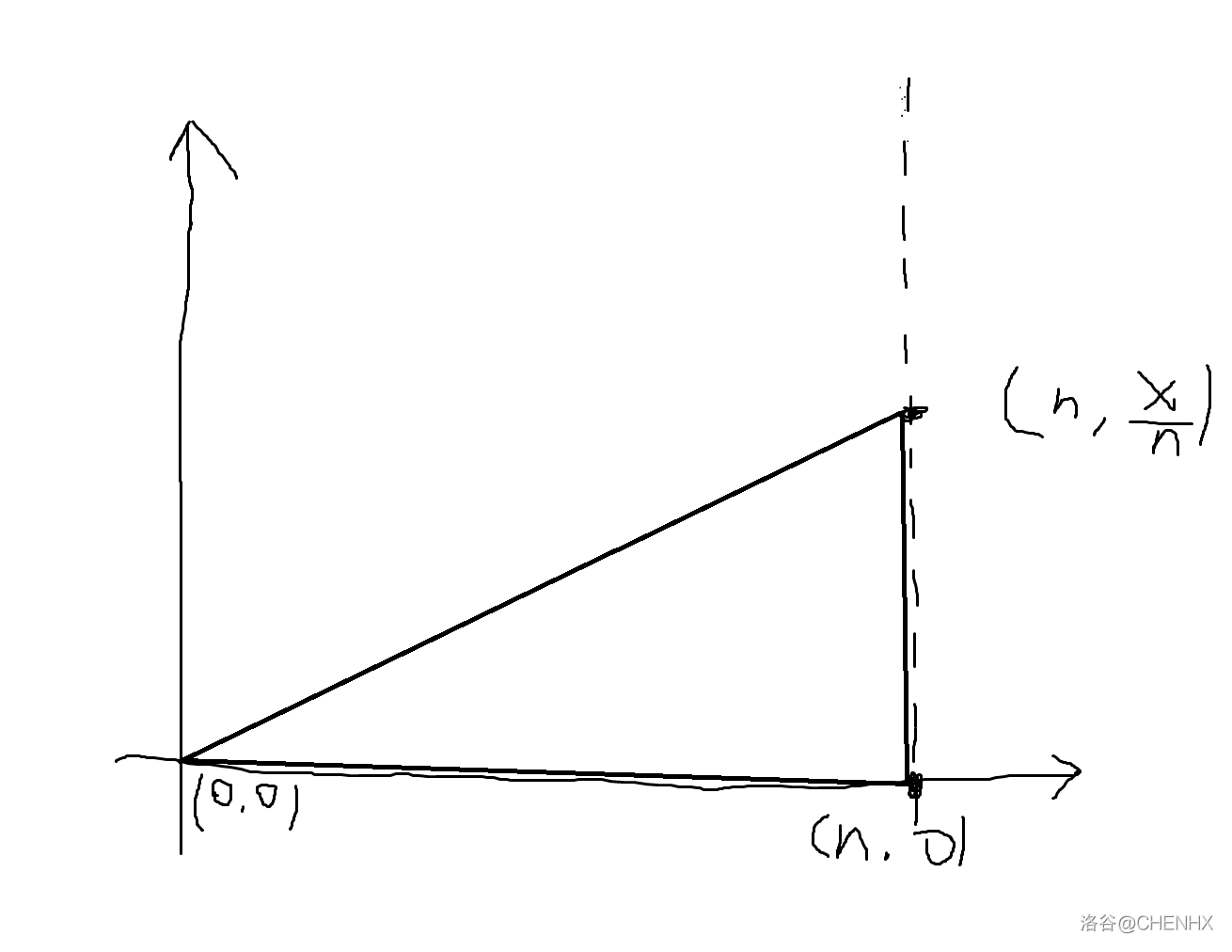
然后把 \((0,0)\) 抬高一个点,这样子这个三角形的底边就是倾斜的了,如下
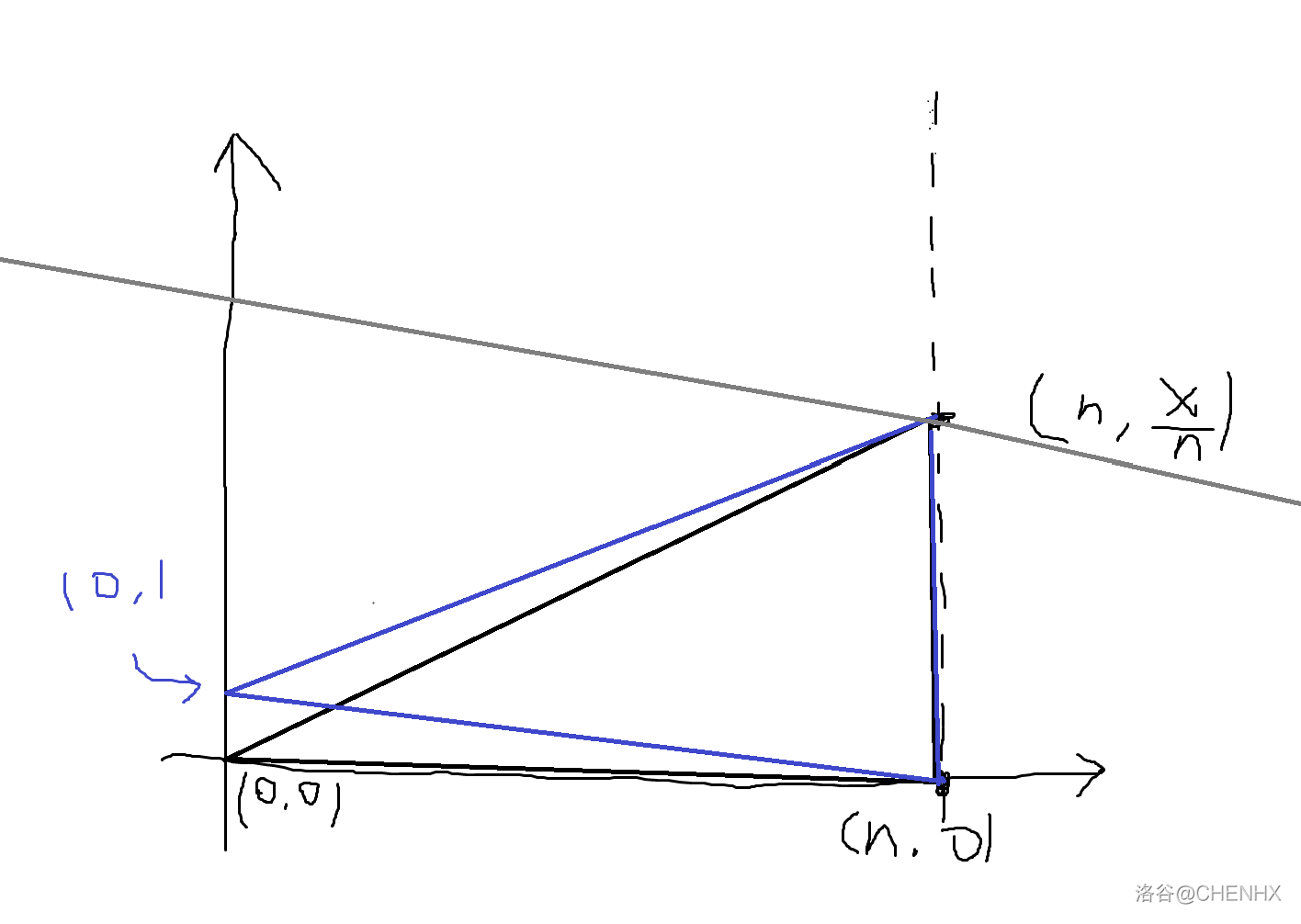
接着右上角的那一个点就可以在灰线上乱滑了,由于斜线的斜率为 \(\frac{1}{n}\) ,就意味着这个点每向 \(x\) 轴挪一个整点,纵坐标就增加了 \(\frac{1}{n}\) 。就这样可以把 \(y\) 坐标调整到 \(\lceil \frac{x}{n} \rceil\) ,如下
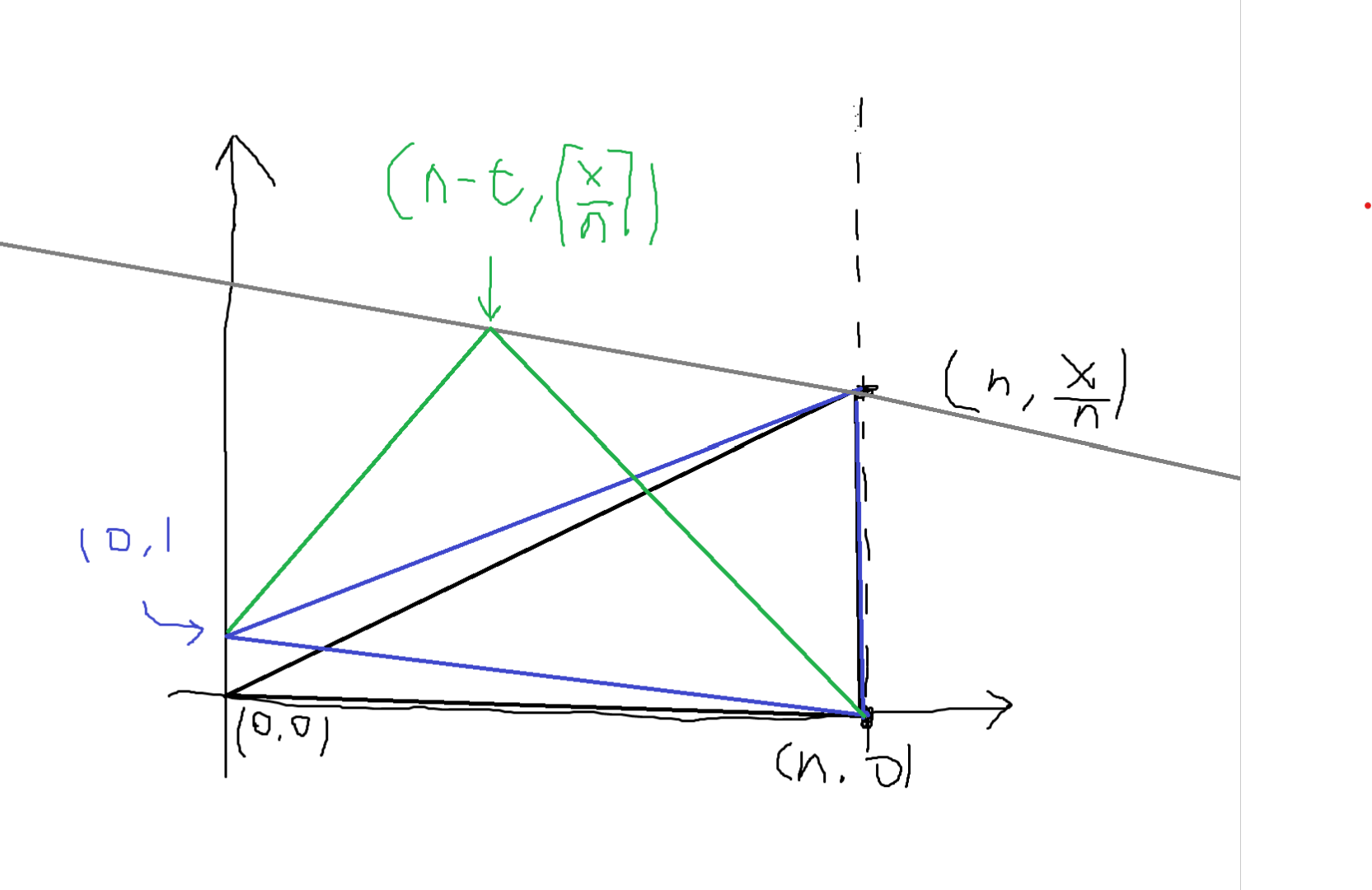
其中 \(t\) 就是向左滑行的量,$t = (\lceil \frac{x}{n} \rceil - \frac{x}{n})\times n $,显然这个 \(t\) 是小于 \(n\) 的,因为 \(\lceil x \rceil - x < 1\) ,然后这个三角形的面积就是 \(\frac x 2\) 的,和题目要求一致。
F
考虑存在偶数边长的情形,那么如下构造
<--even-->
1111111111
1*1*1*1*11
11*1*1*1*1
1*1*1*1*11
1111111111
如果长和宽都是奇数的情形,如果还像上面那样构造,就会出现 \(11*11\) 的情形
这个时候考虑把某个乘号换成加号即可
1 1 1 1 1 1 1 1 1
1 * 1 * 1 * 1 * 1
1 1 + 1 * 1 * 1 1
1 * 1 * 1 * 1 * 1
1 1 * 1 + 1 * 1 1
1 * 1 * 1 * 1 * 1
1 1 * 1 * 1 + 1 1
1 * 1 * 1 * 1 * 1
1 1 1 1 1 1 1 1 1
G
简单网络流,就是二分图匹配,考虑每个左边的点向右边的自己的因子连边权为一边,然后右边的每个数向超级汇点连一个边权为一的边即可
H
最小割,把每个 \(x\) 节点拆成三个点 \(x_1,x_2,x_3\) 然后连边:
对于所有的指向 \(x\) 的边,通过如下方式确定其终点:
-
如果检查站设置在 \(x\) ,那么这个边的指向 \(x_1\)
-
否则这个边指向 \(x_3\)
对于所有从 \(x\) 出发的边,通过如下方式确定其起点:
- 如果检查站设置在 \(x\) ,那么这个边的起点是 \(x_2\)
- 否则这个边的起点是 \(x_3\)
对于每个边,我们有唯一的方式确定了其起点和终点,所以图是确定的(定义是良性的)
然后跑最小割即可。另外注意算法的常数,传说有人的 dinic 被卡了
I
先考虑一个强连通分量里的情形,一个强连通分量能在自身内无限循环的充要条件是
- 在该强连通分量内存在一条边权和不为零的回路
所以可以把这个强连通分量抽出来跑 dfs 生成树即可
然后显然一个强连通分量能无限循环的条件为以下二者之一或者二者全部:
- 这个强连通分量能自身无限循环
- 这个强连通分量能去到无限循环的强连通分量
所以简单跑一下 tarjan 即可
J
我们把每段圆弧看作向量:
那么要做的就是给每个向量的两个分量安排正负使得所有向量之和为零向量
然后先看要求光滑连接这个条件,实际上就是要求 \(n\) 是偶数,因为你总是以正负交替的方式来安排各个圆弧的方向
那么实际上就是要在这 \(n\) 个 \(r\) 中选取若干个使得:
然后你要两个分量都有的选,所以总共要有至少 4 种不同的选法才行,所以就是背包计数
K
分层图+最短路即可