C++专题三学习日记
stack(栈)
仅支持查询或删除最后一个加入的元素(栈顶元素)
| 函数名 | 功能 | 时间复杂度 |
|---|---|---|
| top() | 返回栈顶元素 | O(1) |
| empty() | 判断是否为空 | O(1) |
| size() | 返回元素个数 | O(1) |
| push() | 在栈顶插入元素 | O(1) |
| pop() | 删除栈顶元素 | O(1) |
queue(队列)
仅支持查询或删除第一个加入的元素(队首元素)
| 函数名 | 功能 | 时间复杂度 |
|---|---|---|
| front() | 返回队首元素 | O(1) |
| back() | 返回队尾元素 | O(1) |
| empty() | 判断是否为空 | O(1) |
| size() | 返回元素个数 | O(1) |
| push() | 在队尾插入元素 | O(1) |
| pop() | 删除队首元素 | O(1) |
priority_queue
优先队列 std::priority_queue 是一种堆,一般为二叉堆。
| 函数名 | 功能(默认大根堆) | 时间复杂度 |
|---|---|---|
| top() | 返回最大元素 | O(1) |
| empty() | 判断是否为空 | O(1) |
| size() | 返回元素个数 | O(1) |
| push() | 插入元素 | O(log n) |
| pop() | 删除最大元素 | O(log n) |
priority_queue<int> a;//默认大根堆(从大到小排)
priority_queue<int,vector<int>,greater<int>> a;//小根堆(从小到大排)
ST表
倍增思想,需要预处理log_2和f[i][j]
预处理log_2:
int log_2[N];
log_2[1]=0;
for(int i=2;i<=n;i++){log_2[i]=log_2[i/2]+1;
}
预处理f[i][j]
int f[N][20];
for(int j=1;j<=20;j++){for(int i=1;i<=N;i++){f[i][j]=f[f[i][j-1]][j-1]; //借鉴国旗运动例题,具体情况具体分析}
}
例1):给定n个数,m个询问,对于每个询问了l,r,需要回答区间[l, r]中的最大值或最小值。
ST表基于倍增的思想,可以实现O(nlogn)下进行预处理,并在O(1)时间内回答每个询问。
此题中f[i][j]表示区间[i,i+(2^j)-1]的最大值
#include <bits/stdc++.h>
using namespace std;
const int N=5e6;
int smax[N][31],log_2[N];
int main(){int n,m;cin>>n>>m;log_2[1]=0;for(int i=2;i<=n;i++){log_2[i]=log_2[i/2]+1;//预处理log2}//也可以直接用以下函数计算log2,头文件为#include <cmath>//_lg(m):计算以2为底的对数,接受一个整数,返回一个整数//log2(m):计算以2为底的对数,接受一个参数(不一定要是整型),返回一个double、float 或for(int i=1;i<=n;i++){cin>>smax[i][0];//smax[i][0]即区间(i,i)的最大值,即i}for(int j=1;j<=log_2[n];j++){for(int i=1;i+(1<<j)-1<=n;i++){smax[i][j]=max(smax[i][j-1],smax[i+(1<<(j-1))][j-1]);}}int l,r;for(int i=1;i<=m;i++){cin>>l>>r;int s=log_2[r-l+1];cout<<max(smax[l][s],smax[r-(1<<s)+1][s])<<endl;}return 0;
}
做题日记
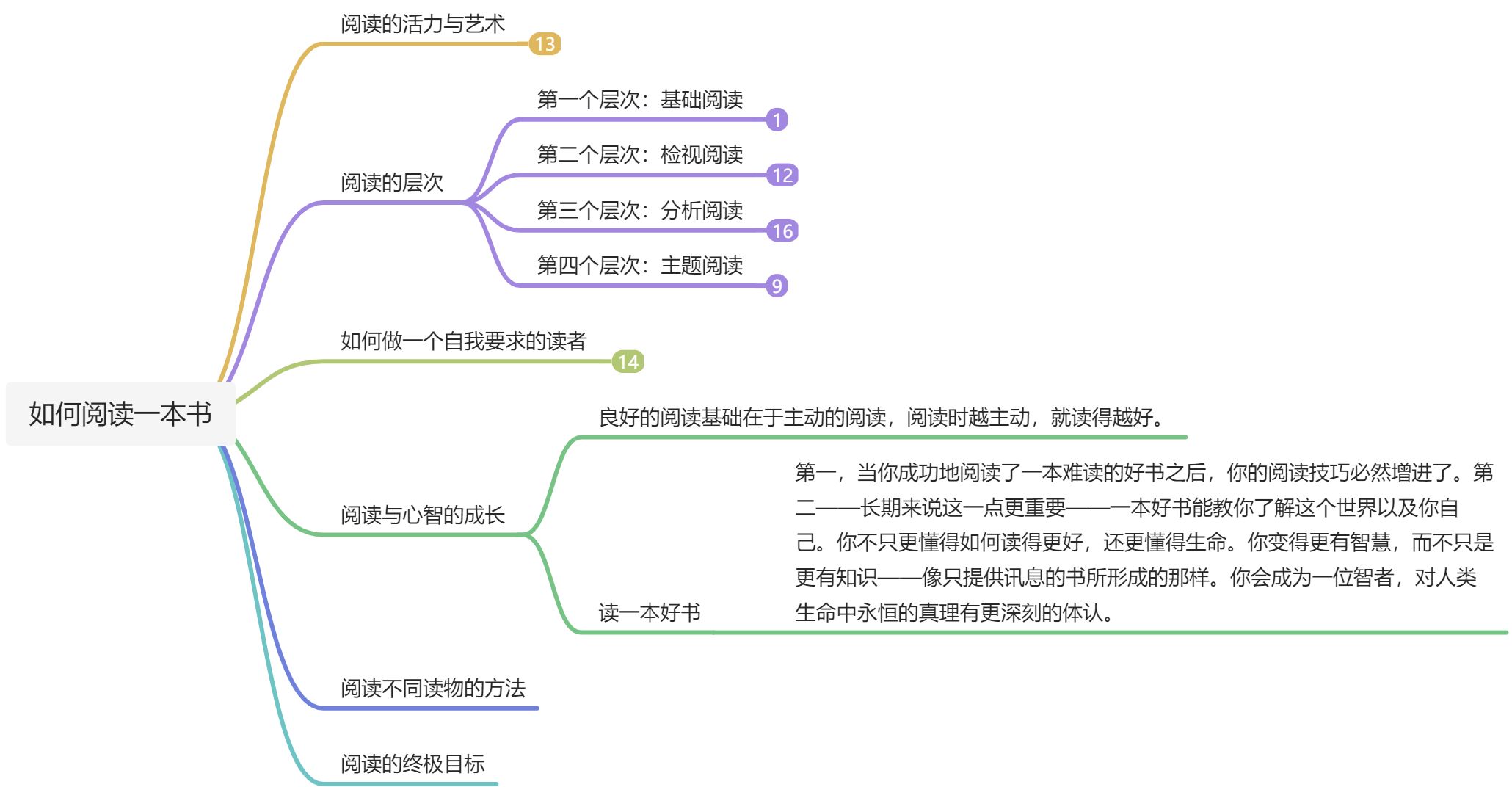
1.国旗计划
#include<bits/stdc++.h>
using namespace std;
const int N=2e6;
int n,m;
int ans[N]; //储存答案
int f[N][20]; //f[i][j]表示从i起跳,跳2^j区间后站的位置
struct node{int id;int l,r;
}s[N*2]; //化环为链,二倍链思想
bool paixu(node a,node b){return a.l<b.l; //每个战士按左端点从小到大排
}
void solve(int k){int rr=s[k].l+m;int tt=1; //表示已使用1个区间int p=k;for(int i=19;i>=0;i--){ //倒序遍历所有倍增级别,尝试尽可能多的跳跃,直到覆盖目标rrif(f[k][i]!=0&&s[f[k][i]].r<rr){ tt+=(1<<i); //如果从当前区间k跳2^i步后,所到达的区间右端点仍然小于rr,则可以选择这一次跳跃,累加tt,更新kk=f[k][i];}}ans[s[p].id]=tt+1;
}
int main(){cin>>n>>m;int i;for(i=1;i<=n;i++){cin>>s[i].l>>s[i].r;if(s[i].r<s[i].l)s[i].r+=m;s[i].id=i;}sort(s+1,s+1+n,paixu); //排序for(i=1;i<=n;i++){s[i+n]=s[i];s[i+n].l=s[i].l+m;s[i+n].r=s[i].r+m;} //部署二倍链int p;for(i=1,p=i;i<=2*n;i++){while(p<=2*n&&s[p].l<=s[i].r){p++;}f[i][0]=p-1; //找到每个战士对应的下一个战士,满足下一个战士的左端<=这个战士的右端}for(i=1;i<20;i++){for(int j=1;j<=2*n;j++){f[j][i]=f[f[j][i-1]][i-1];}} //ST表,倍增for(i=1;i<=n;i++){solve(i);}for(i=1;i<=n;i++){cout<<ans[i]<<' ';}return 0;
}
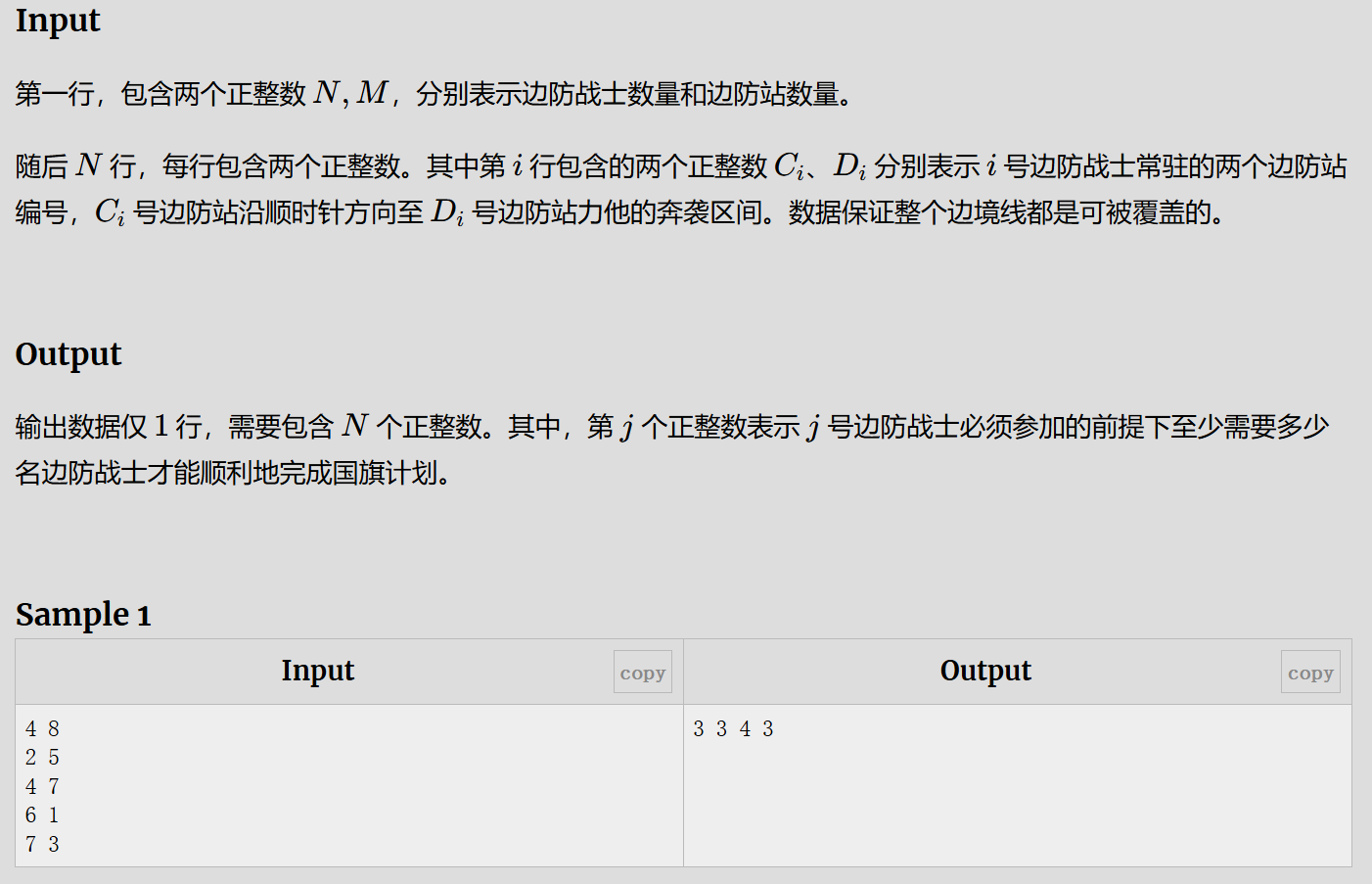
2.约瑟夫环问题
#include<iostream>
#include<queue>
using namespace std;
int main(){int n,m;cin>>n>>m;queue<int> a;int i;for(i=1;i<=n;i++){a.push(i);}int id=0;while(!a.empty()){id++;int t=a.front();a.pop(); //弹出队首元素,符合条件就输出,不符合就再入队,变成队尾元素if(m==id){cout<<t<<' ';id=0;}elsea.push(t);}return 0;
}