CF70E Information Reform
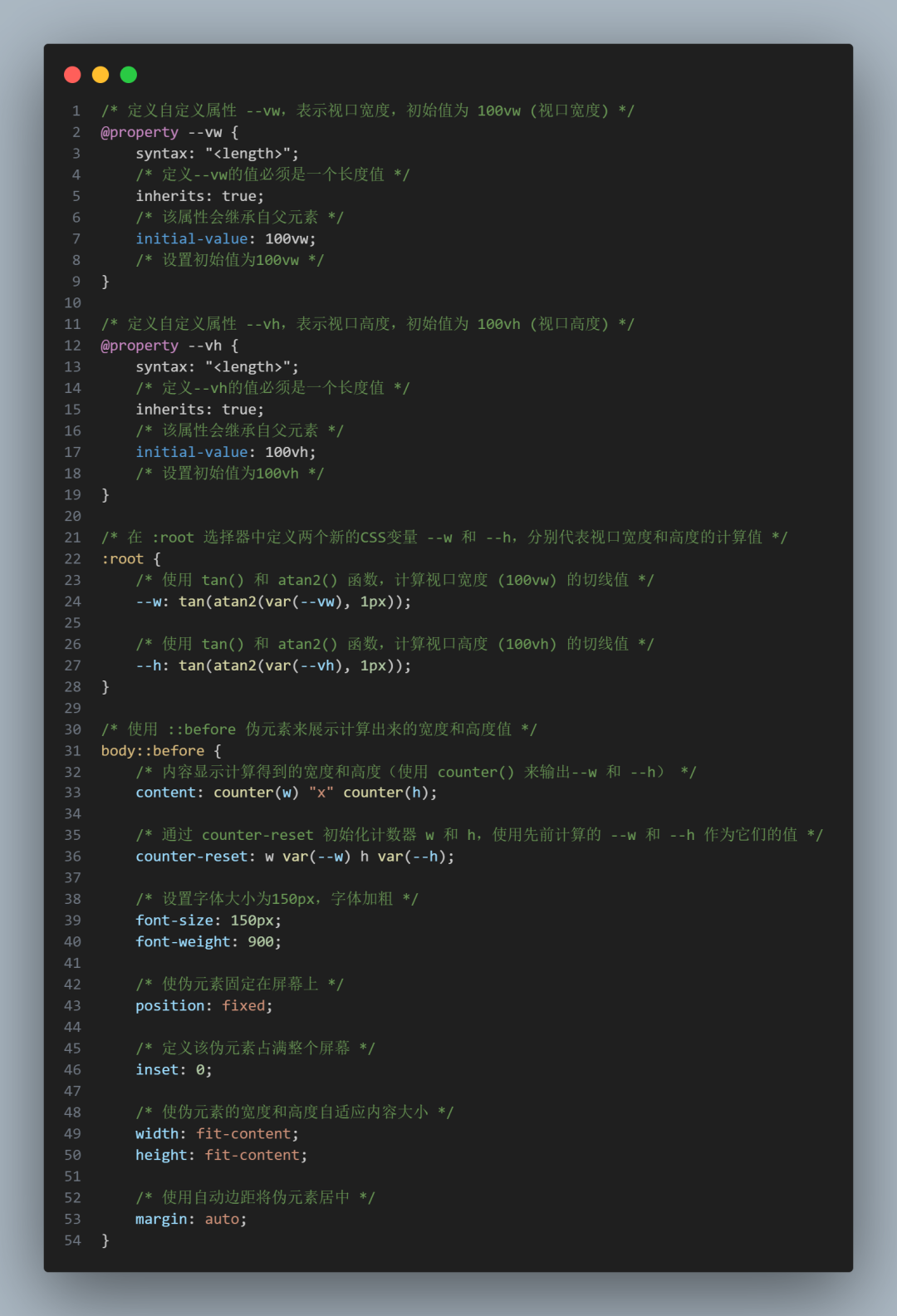
树形 DP 好题。一开始想成了换根,想了 2h 发现不太可做,主要是不会设计状态。套路地将节点 \(u\) 选还是不选设入状态这种方法是不可做的。
观察到 \(n\le180\),在树上问题中这个数据范围不多见,大抵是一个 \(O(n^3)\) 的算法,那么首先不管用 Floyd 还是 DFS 求出两点间距离记作 \(\text{dis}(u,v)\) 是容易的。
那么状态设计就是本题的难点,首先得到一个极为重要的引理如下。这个引理告诉我们,对于一个节点 \(u\) 所辐射的点形成一个连通块。那么既然形成了一个连通块了,就可以将问题转化为:把树分为若干个连通块,每个连通块选择一个区域信息中心的代价。
引理:设 \(t_i\) 是离节点 \(i\) 最近的区域信息中心。对于树上两点 \(u,v\),若 \(t_u=t_v=k\),则在 \(u\to v\) 路径上的所有点 \(w\) 都满足 \(t_w=k\)。
那么这个问题就简单了,对于每个连通块在其根部计算贡献,设 \(f_{u,j}\) 为以 \(u\) 为根的子树中 \(t_u=j\) 的最小代价,则有
\[f_{u,j}\gets f_{u,j}+\min_{v\in\text{son}(u)}\{f_{v,k},f_{v,j}-K\}
\]
实际实现中,我们只需要再记录一个使 \(f_{u,j}\) 最小的 \(j\),记作 \(g_u\),就可以把上述转移方程优化到 \(O(n^3)\)。
输出方案也是容易的。
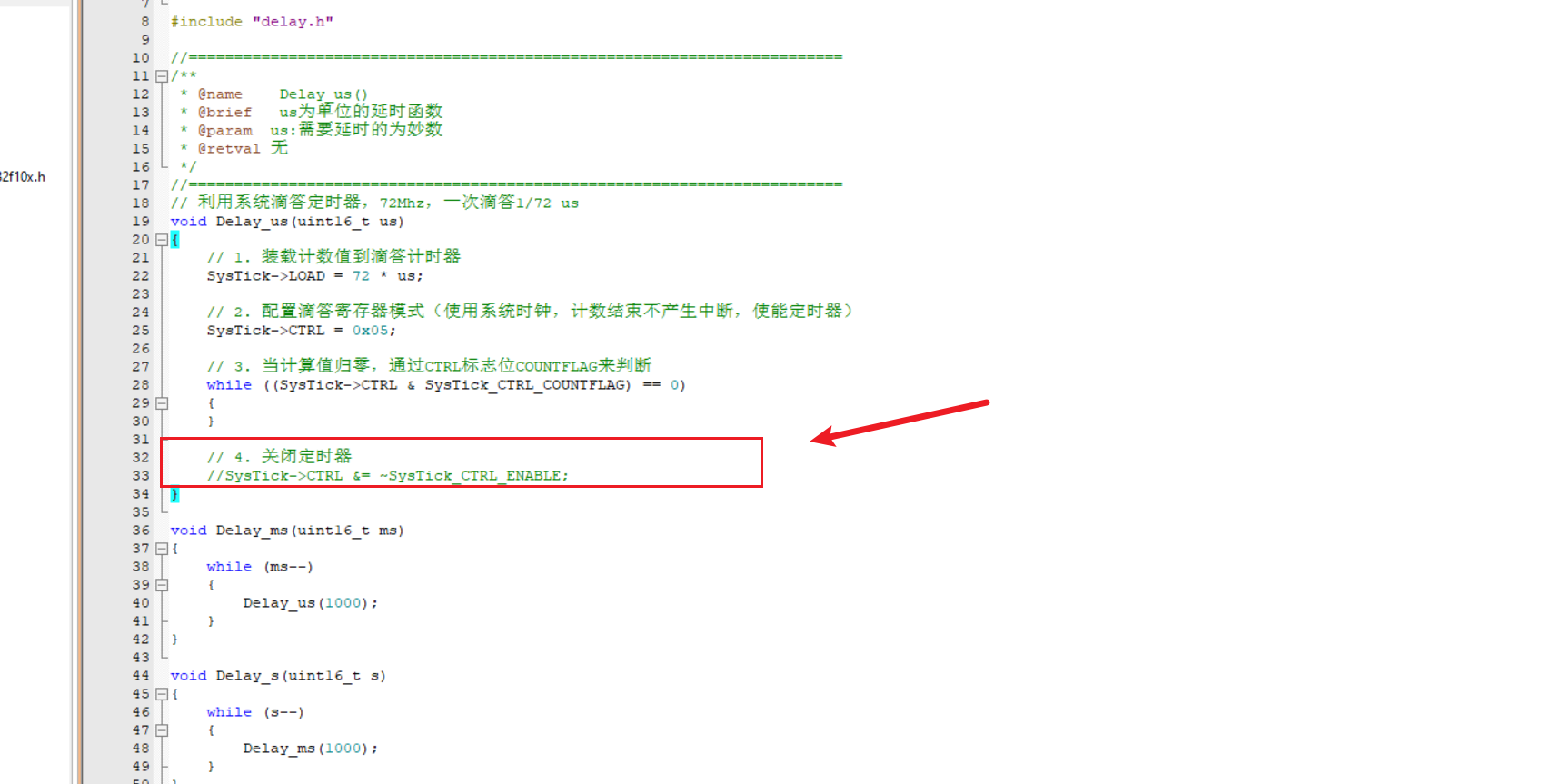
#include<bits/stdc++.h>
using namespace std;constexpr int MAXN=205;
int n,k,d[MAXN],dis[MAXN][MAXN];
vector<int>G[MAXN];
int f[MAXN][MAXN],g[MAXN],ans[MAXN];void getdis(){for(int k=1;k<=n;++k)for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
}
void dfs(int u,int fno){memset(f[u],0x3f,sizeof(int)*(n+5));for(int i=1;i<=n;++i) f[u][i]=d[dis[u][i]]+k;for(auto v:G[u]){if(v==fno) continue;dfs(v,u);for(int i=1;i<=n;++i)f[u][i]+=min(f[v][i]-k,f[v][g[v]]);}for(int i=1;i<=n;++i) if(f[u][i]<f[u][g[u]]) g[u]=i;
}
void dfs2(int u,int fno){for(auto v:G[u]){if(v==fno) continue;if(f[v][ans[u]]-k<f[v][g[v]]) ans[v]=ans[u];else ans[v]=g[v];dfs2(v,u);}
}int main(){cin.tie(nullptr)->sync_with_stdio(0);cin>>n>>k;for(int i=1;i<n;++i) cin>>d[i];memset(dis,0x3f,sizeof(dis));for(int i=1;i<=n;++i) dis[i][i]=0;for(int i=1,u,v;i<n;++i){cin>>u>>v;G[u].emplace_back(v);G[v].emplace_back(u);dis[u][v]=dis[v][u]=1;}getdis();dfs(1,0);cout<<f[1][g[1]]<<'\n';ans[1]=g[1];dfs2(1,0);for(int i=1;i<=n;++i) cout<<ans[i]<<" \n"[i==n];return 0;
}