2/9 关于费用流 dp数组的大小

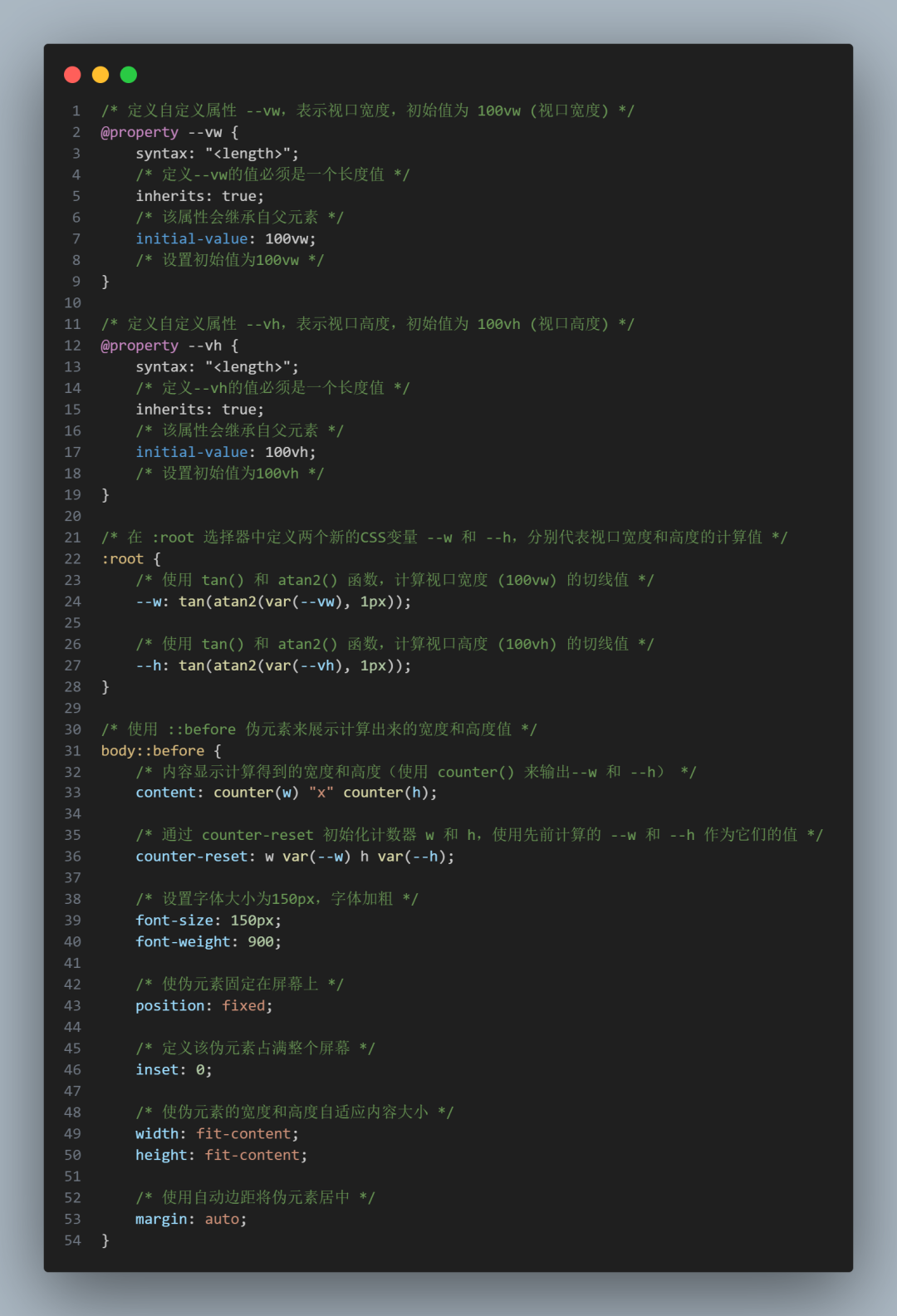
实际上是2/8的事情了，懒鬼今天才发（

问题来源是P1004和P1006两题

费用流dp数组（假设是三维dp [ k ][ i ][ j ]）
k的大小应该开到最少n+m-1

DeepSeek大导师给的说明如下：

用户可能在方格取数问题中，使用三维的dp数组，其中第一维是k，第二维是i，第三维是j。例如，dp[k][i][j]，其中k的范围是0到2n-2。例如，当n=9时，k的最大是16，所以dp数组的第一维需要至少17个元素。如果用户将第一维的大小设为11*2=22，那么足够。而传纸条的问题中，当n和m是50时，k的最大是50+50-2=98，所以第一维需要99个元素。如果用户将传纸条的dp数组的第一维设为55，那么当k超过55时就会越界。这时候，将第一维的大小扩大到100就能解决问题。

在动态规划问题中，越界问题通常源于状态数组的维度不足而非数据数组的大小。以下是关键点：

1. 状态转移的范围分析：

   • 方格取数（N×N）：最大步数 k = 2N-2。若 N=9，则 k_max=16。状态数组 dp[k][i][j] 的 k 维度需至少 17。用户设置 11*2=22 足够。
   • 传纸条（N×M）：最大步数 k = N+M-2。若 N=M=50，则 k_max=98。原 dp[55][55][55] 的 k 维度仅 55，导致越界。扩大至 100 后解决。

2. 数据数组的安全访问：

   • 当 k 合法时，i 和 j 的取值会被约束在有效范围内（如 i ≤ N），因此 maps 数组只需开 N×N 或 N×M 即可，无需额外扩大。

结论：确保动态规划数组的维度足够覆盖所有可能的步数，而非盲目扩大数据数组。正确计算 k 的最大值并据此设计数组大小是关键。