ACM寒假集训第四期

ACM寒假集训第四期

有理数取余

思路

bx=a mod m

x=((a mod m) * ( b^(-1) ) mod m)) mod m;

问题就转化为如何求解 b 的逆元

b x = 1 mod m ,b对m的逆元，当 gcd(b,m)=1 时才存在。存在 bx+my=1

通过辗转相除法可以得到b,m的最大公约数然后根据最后得到的一系列等式合并为 bx+my=1的形式，则x就是b对m取模的逆元，再带入等式即可求出

这道题应该注意输入的数据非常的大，所以需要通过字符串来输入，然后逐步取模缩小数据范围（本题因为本来就要求结果取模值，所以前面的一些数据也可以取模）

X=X*10+o 解释：X是当前值，o是当前值的末位补一位后的个位的值

代码

#include<iostream>
using namespace std;
const long long m=19260817;
struct bend{long long x,y;bend(long long x=0,long long y=0):x(x),y(y){}
};
bend ds(long long a,long long b){if(1==(a%b)) return bend(1,a/b);bend tem=ds(b,a%b);return bend(-tem.y,-(tem.x+a/b*tem.y));
} 
long long gcd(long long a,long long b){if(a%b==0) return b;return gcd(b,a%b);
}
inline void read(long long &X)
{X = 0;char O = getchar();while (O < '0' || O > '9') O = getchar();while (O >= '0' && O <= '9'){X = ((X << 1) + (X << 3) + (O ^ 48)) % m;//输入有点大,特殊处理一下 //x*2+x*2+(o-48)O = getchar();}
}
int main(){long long a,b,re_b=0;//先假设a>b; bend ans;long long max,min;read(a),read(b);long long g=gcd(a,b);a/=g,b/=g;if(m>b) max=m,min=b;else max=b,min=m;g=gcd(max,min);if(g!=1){cout<<"Angry!";return 0; }if(b<m){ans=ds(m,b);if(ans.y<0) re_b=-ans.y;else re_b=-(ans.y%m)+m;}else{ans=ds(b,m);if(ans.x<0) re_b=-ans.x;else re_b=-(ans.x%m)+m;}cout<<((a%m)*(re_b%m))%m;return 0;
} 

Minimal Coprime

思路

质数区间相邻的两个数之间必定是质数区间，就考虑区间长度为0时是否存在质数区间，区间长度为0时，只有[1,1]这个区间符合条件，所以要特殊考虑，当大区间就是[1,1]时，只有一个最小质数区间，cnt=1,除此之外都是相邻两个数之间构成一个最小质数区间cnt=r-l

代码

#include<iostream>
using namespace std;int main(){int t;cin>>t;while(t--){int l,r,cnt=0;cin>>l>>r;if(l==1&&r==1) cnt=1;else cnt=r-l;cout<<cnt<<endl;}	return 0;
}

素数密度

思路

论时间复杂度当然是线性筛的方法能够更快的得到一段区间中素数的个数，但是这种方法受限于内存的大小，当内存超过百万级别基本上就很难实现。

任何一个大于一的正整数都可以用质数积唯一的表示，一个数字R的因子一定位于[2,sqrt(R)]这个范围中，所以说任何一个大于等于2的数字R的最小质因子一定位于[2,sqrt(R)]中，通过最小质因子的倍数也就是埃式法就可以去掉以这个最小质因子为因子的所有合数，如果确定一个区间[l,r]的素数的个数，可以将这个区间所有的合数全部都去掉，我只需要直到[2,sqrt(r)]这段区间的所有素数，就可以用取倍数的方法去掉[l,r]这个区间的所有合数。

直接开一个大小为r的数组太大了，但是我们知道给定的区间的大小必定不超过百万级别，所以我们可以通过加一个偏移变量的方式用大小为 r-l+1大小的数组来表示[l,r]范围的值。这样就可以更快的得到给定区间内

代码

#include<iostream>
#include<cmath>
using namespace std;
#define ll long long
const int MAX=1100000;
int prime[MAX],cnt=0,l,r;
int is_c[MAX];
int ans[MAX];
void pre() {//线性筛选for (int i = 2; i <= 50000; ++i) {if (!is_c[i]) prime[cnt++] = i;for (int j = 0; j < cnt;++j) {int p = prime[j];if (i * p > 50000)break;is_c[i * p] = 1;if (i % p == 0) break;}}
}
int main() {ll l, r;cin >> l >> r;l = l == 1 ? 2 : l;pre();for (int i = 0; i < cnt; ++i) {ll p = prime[i],start = (l - 1 + p) / p * p > 2 * p ? (l - 1 + p) / p*p : 2 * p;//因为p是素数，所以不应该被标记，而是至少从2p开始for (ll j = start; j <= r; j += p) ans[j - l + 1] = 1;}int cnt_ans=0;for (int i = 1; i <= r - l + 1; ++i) {if (ans[i] == 0) ++cnt_ans;}cout << cnt_ans;return 0;
}

最大公约数和最小公倍数问题

思路

两个数字做短除法

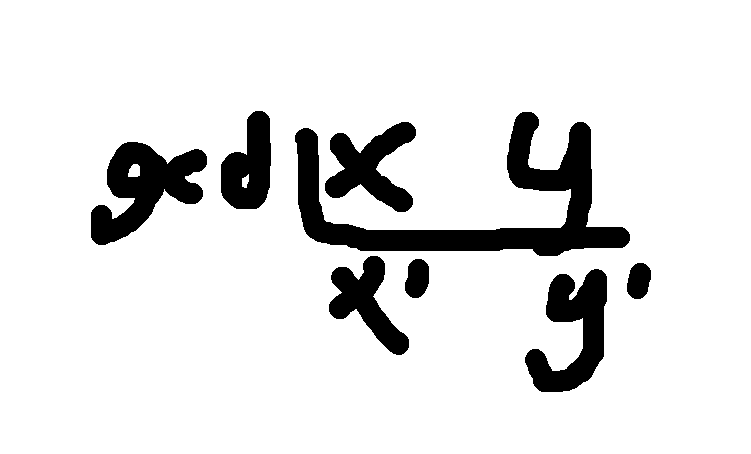
当gcd(x',y')=1时，得cd就是最大的，并且我们知道，最小公倍数lcm=gcd*x' * y' ,

所以 x' * y'= lcm/gcd; gcd | lcm

所以我们只需要看 lcm/gcd结果的互质因子对有几个就是有多少组P,Q

代码

#include<iostream>
#include<cmath>
using namespace std;
int gcd(int a, int b) {if (!(a % b)) return b;return gcd(b, a % b);
}
int main() {int d, m, diff,cnt=0;cin >> d >> m;if (d > m || m%d) {cout << 0;return 0;}diff = m / d;//两个数字的 最大公约数 | 最小公倍数 可以通过短除法看出//剩下有几对P,Q就看有几对互质数相乘等于diff,注意P==Q的情况for (int i = 1; i <= sqrt(diff); ++i) {if (!(diff % i)&&gcd(i,diff/i)==1) {//i | diff,同时 i与diff/i互质if (i == diff / i) ++cnt;else cnt += 2;}}cout << cnt;return 0;
}

Longest Subsequence

思路

可以想到，最小公倍数一定大于其所有的因子，所以为了方便来看区间和最小公倍数的关系，我们可以对整个区间进行排序，但这样就打乱了位置顺序，而结果需要我们来输出位置信息，所以我们需要给每一个数据同时记录位置信息，然后根据数值大小进行排序

一个数字不存在公倍数的说法，至少两个数字之间才会有公倍数的说法，所以可以求解出一个数字的倍数有哪些，还可以求出另一个数字的倍数有哪些，这两组数列中率先相等的值就是这两个数字的最小公倍数。

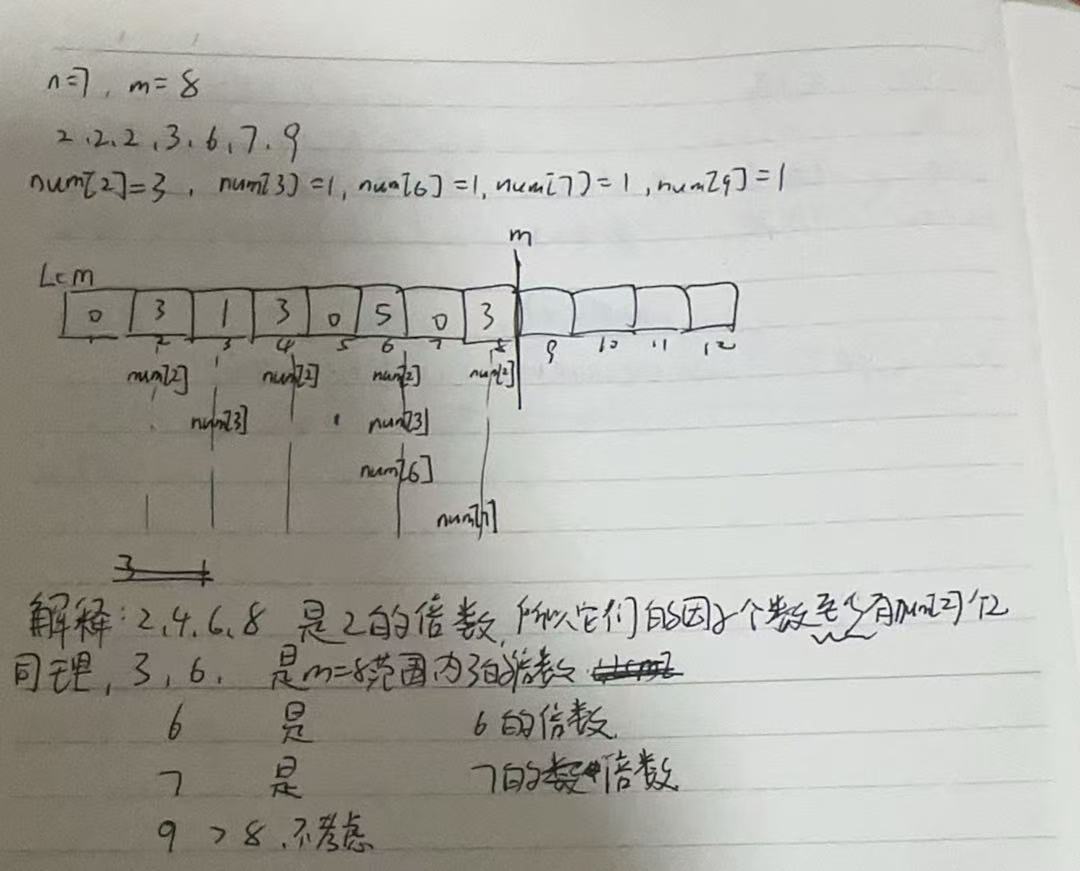
可以用num[]数组来记录每一个数字有几个，例如num[2]=3,就表示给定的数列中，数值大小等于2的有三个

用另一个数组lcm[]来记录以此下标为倍数的数字的个数，例如lcm[6]=5,就表示数字6是给定序列中5个数字的倍数。优先选择lcm数字小的lcm[lc]的最大值，来保证数字6也是这5个数字的最小公倍数，至少后面可能会出现同样是这几个数字的公倍数，但后面的一定不是最小的，但可能lcm[]的数值更大，因为他可能还是其他数字的公倍数，我们确定了在m范围内，lcm[]值最多的最小公倍数后，取原来的数列中来看这个lc是哪些数字的最小公倍数，并将这些数字的位置记录在另一个数组中，但是这个数组一开始记录的位置信息是随机的，所以我们还需要对这个位置数组进行排序，使其变为升序。

代码

#include<iostream>
#include<algorithm>
#include<climits>
using namespace std;
#define PII pair<int,int>
#define MAX 1000001
int n, m;
PII a[MAX];
int num[MAX],lcm[MAX];
int lc, cnt = INT_MIN, ans[MAX];
void solve() {cin >> n >> m;for (int i = 1; i <= n; ++i) {cin >> a[i].first;//表示数值a[i].second = i;//表示编号}std::sort(a + 1, a + 1 + n);for (int i = 1; i <= n; ++i) {if (a[i].first > m) continue;++num[a[i].first];}for (int i = 1; i<=n&&a[i].first<=m; ++i) {if (a[i].first == a[i - 1].first) continue;for (int j = a[i].first; j <= m; j += a[i].first) {lcm[j] += num[a[i].first];}}for (int i = 1; i <= m; ++i) {if (cnt < lcm[i]) {cnt = lcm[i]; lc = i;}}if (cnt == 0) {cout << 1 << " " << 0;return;}for (int i = 1,j=0; i <= n; ++i) {if (lc % a[i].first == 0) ans[j++] = a[i].second;}sort(ans, ans + cnt);cout << lc << " " << cnt << endl;for (int i = 0; i < cnt; ++i) {cout << ans[i];if (i != cnt - 1) cout << " ";}
}
int main() {ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);//这行啥意思int T = 1;//cin >> T;while (T--) solve();return 0;
}

Common Generator

思路

x+d=y,同时d是x的因子说明d是x,和y的公因子 ，x=k*d , 则 y=(k+1)d

由此我们可以推断出 2 是所有偶数的生成数

如果一个数字是奇数y,他是有x+d得到的，如果d是y的因子，y为奇数，说明d也为奇数，所以x=y-d，x必定为偶数，所以如果y是一个奇合数，那么2可以得到任何一个偶数x，然后通过这个偶数x和y的公因子d就可以得到奇合数y，所以数字2可以得到任何一个合数。

所以如果一个数列中全是合数，那么答案就可以是2

那么这串数列中出现了质数又是怎样的结果呢？

当这串数列中质数的个数大于等于2时，这串数列就不能被生成。因为假设存在一个生成数ans可以生成质数x，那么ans不能是1那这个ans肯定就是第一个质数x，那么质数x可以生成另一个质数y吗？质数与其他任何数字的公因子都只有1，所以不可能由其他数字得到，只能由自己经过0次变化得到，但是ans已经是x了，所以当这个数列中的质数的个数大于等于2时无解

当这个数列中只有1个质数时就不会产生生成这个质数的冲突，并且如果能够生成这个质数，则需要ans就等于这个唯一的质数，但是这个质数是否能生成其他的数列中的数字呢？

我们对此还是根据奇数和偶数的不同来讨论

ans是个质数，所以他的大于2的因子只有本身，所以经过一次变换后变为2ans，但是2ans能否表示出其他的数字呢？

2ans有公因数因数2，所以他一定可以表示出大于等于2ans的所有偶数，但是小于他的偶数肯定表示不出来

然后来看奇数，这个奇数一定时通过一个偶数加上他的他俩的公因子得到的，还是跟上面一样，y=x+d,y是奇数，那么因子d也肯定是奇数，那么奇数-奇数得到的x就是偶数，那么问题就变成了偶数 y-d是否能被2ans表示。如果y-d的值越大越可能被表示，所以我们来找y的最小奇因子，我们知道任何一个大于1的正整数都能唯一的表示成素数积的形式，所以y的最小奇数因子一定是质数，因为如果他这个奇数不是质数的话，那么这个奇数还能被分解成质数积的形式，最终y的最小奇因子一定就是他的最小质因子，我们从素数表中遍历得到y的最小质因子，然后如果y-d >=2ans，就说明奇数y可以被ans生成，但是如果y-d< 2*ans那么说明y不能被ans生成

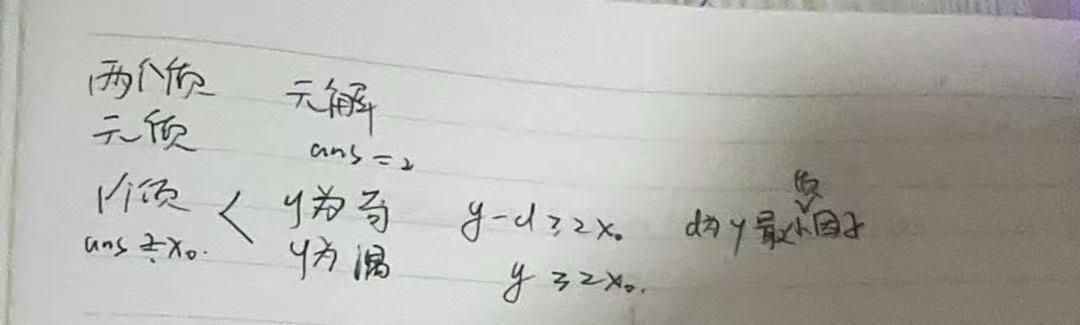
代码

#include<iostream>
#include<vector>
using namespace std;
const int MAX=100001;
int n,a[MAX],cnt=-1;
vector<int> primes;
bool is_c[4*MAX+1];
void liner_test() {//线性筛is_c[1] = 1;for (int i = 2; i <= 4*MAX; ++i) {if (is_c[i]==0) primes.push_back(i);for (auto p : primes) {if (i * p > 4 * MAX) break;is_c[i * p] = 1;if (i % p == 0) break;}}
}
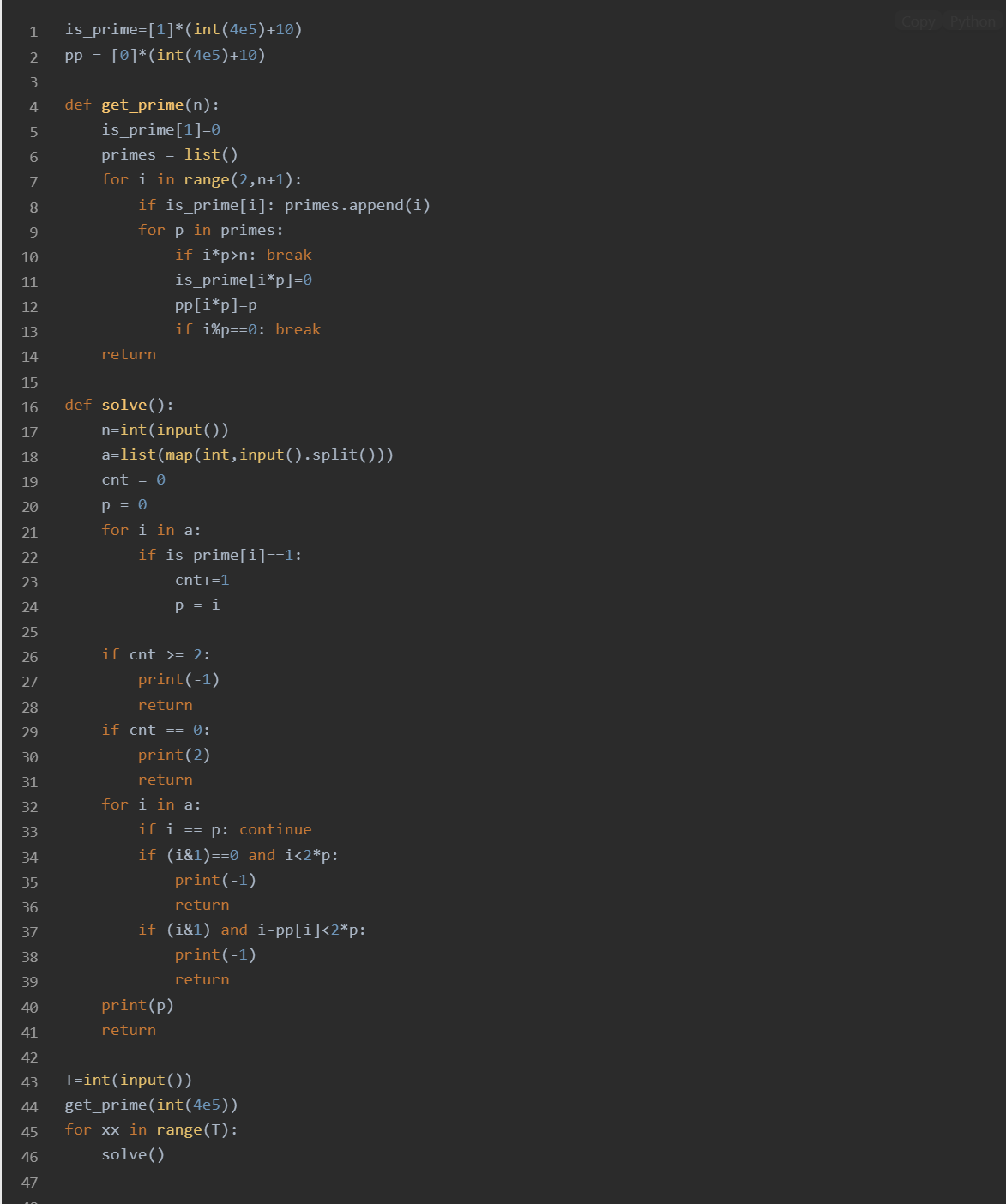
void solve() {cin >> n;for (int i = 0; i < n; ++i) cin >> a[i];int ans=0;for (int i = 0; i < n; ++i) {if (!ans && !is_c[a[i]]) ans = a[i];else if (ans && !is_c[a[i]]) {cout << -1 << endl;return;}}if (ans == 0) {//全是合数cout << 2 << endl;return;}else if(ans){//有且仅有一个质数for (int i = 0; i < n; ++i) {if (a[i] == ans) continue;if (a[i] % 2) {//a[i]是奇数//先找到最小质数因子for (auto p : primes) {if (a[i] % p == 0) {if ((a[i] - p) < 2 * ans) {cout << -1 << endl;return;}else break;//如果这里不break就可能使得a[i]-p的结果偏小，输出-1}}}else if(a[i]<2*ans) {//如果a[i]是偶数cout << -1 << endl;return;}}cout << ans << endl;}
}
int main() {ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);int T = 1;cin >> T;liner_test();//预处理，得到所有的素数合数信息while (T--) solve();return 0;
}

学习总结

线性筛获取区间[2,n]的素数的个数

#include<vector>
vector<int> primes;
bool is_c[MAX];
for(int i=2;i<=n;++i){if(!is_c[i]) primes.push_back(i);for(auto p:primes){if(i*p>n) break;is_c[i*p]=true;if(i%p) break;}
}

埃式筛选法的缺点在于同样一个合数可能被多个素数筛选出来，线性筛保证这些数字只被其中一个素数筛选出来。