欧拉角和四元数，3D 游戏开发中“旋转”难题的通俗讲解和应用实战

news/2025/2/15 11:16:49/文章来源:https://www.cnblogs.com/obullxl/p/18716664/NTopic2025021401

春节期间，老牛同学学习使用 Cocos Creator 研发了一款 3D 小游戏。开发过程中遇到了一些全新概念和用法，虽然借助大模型最终完成了小游戏功能的开发，但对这些概念却一知半解。

其中，在需要 3D 组件旋转的功能中，“欧拉角”和“四元数”就是研发过程中遇到的一个全新的概念。如下代码是大模型帮忙实现的“左右水平滑动”功能：

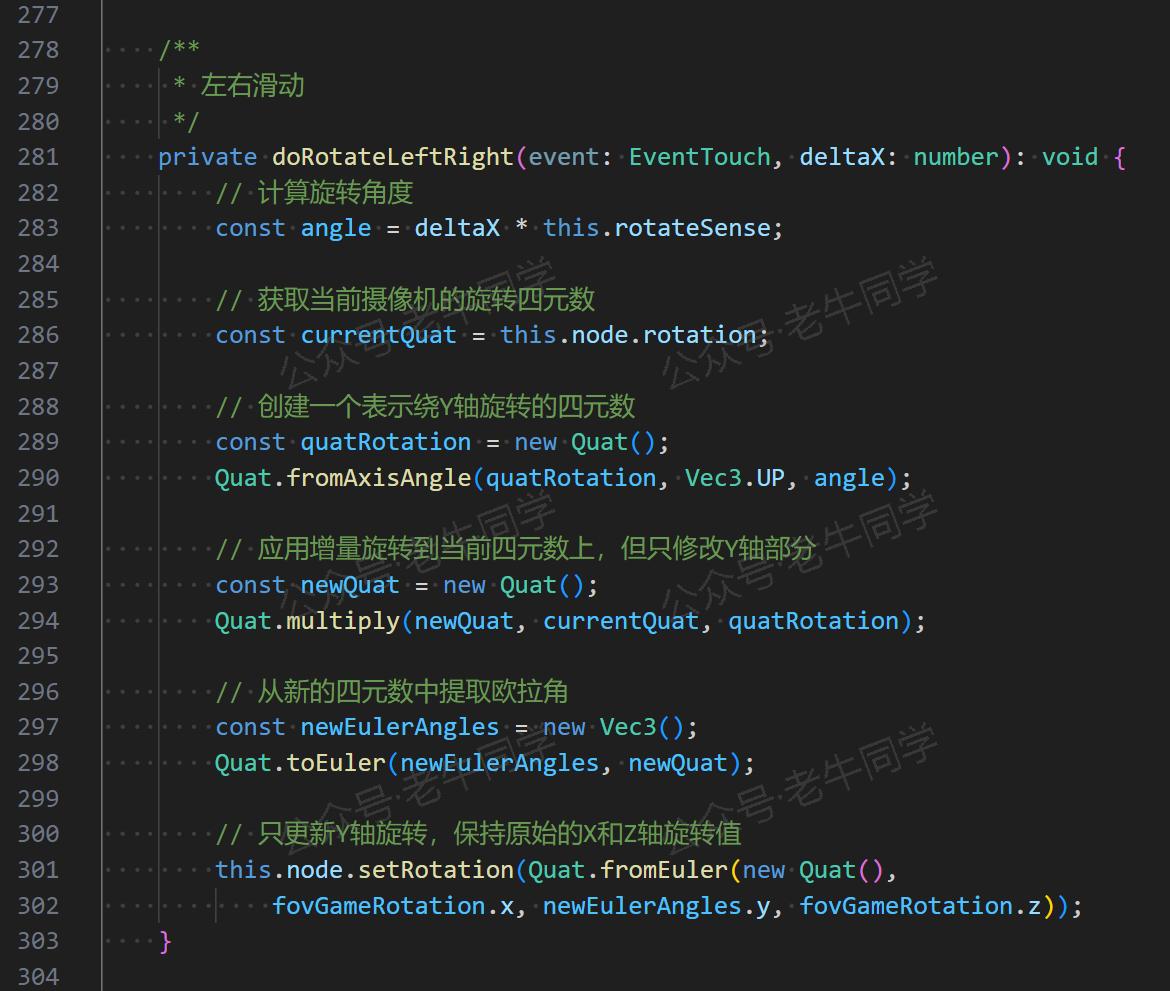
旋转代码样例

本文将对“欧拉角”和“四元数”进行尽可能详细的总结，尽可能不涉及数学证明公式，希望能给像我一样有困惑的朋友一些帮助：

基本概念：为什么对于 3D 物体旋转，大家都采用欧拉角和四元数来表示？为什么 1 个概念还不够，还需要 2 个？他们分别解决什么主要问题？
如何应用：在不同场景下，欧拉角和四元数如何应用旋转？它们如何应用到物体旋转？
实际应用：最后，用一个“让立方体的对角线垂直于地面并旋转”功能，演示如何让物体旋转后并不停的旋转起来。

本文代码和小游戏源代码均可免费下载：打开“老牛同学”微信小程序->点击“更多”Tab->“源代码”获取下载链接。

微信小程序：老牛同学

欧拉角和四元数存在的意义是什么？

首先，欧拉角和四元数都是用于描述三维空间中物体旋转的常用工具，它们只是工具，核心就是三维和旋转。

欧拉角最早由瑞士数学家莱昂哈德·欧拉（Leonhard Euler）于 18 世纪提出，他认为：三维空间中物体的任意姿态，都可以通过三个连续的旋转角度来描述（即：第一步绕某个轴旋转，第二步绕另一个轴旋转，第三步绕第三个轴旋转）。用 3 个数就可以表示旋转姿态，确实一种非常直观且易于理解的方法。

那么，对应到游戏开发中，欧拉角的就是我们最常见的X 轴、Y 轴和Z 轴旋转属性来表示了。如下所示，把一个长方体按照 X/Y/Z 旋转后的姿态：

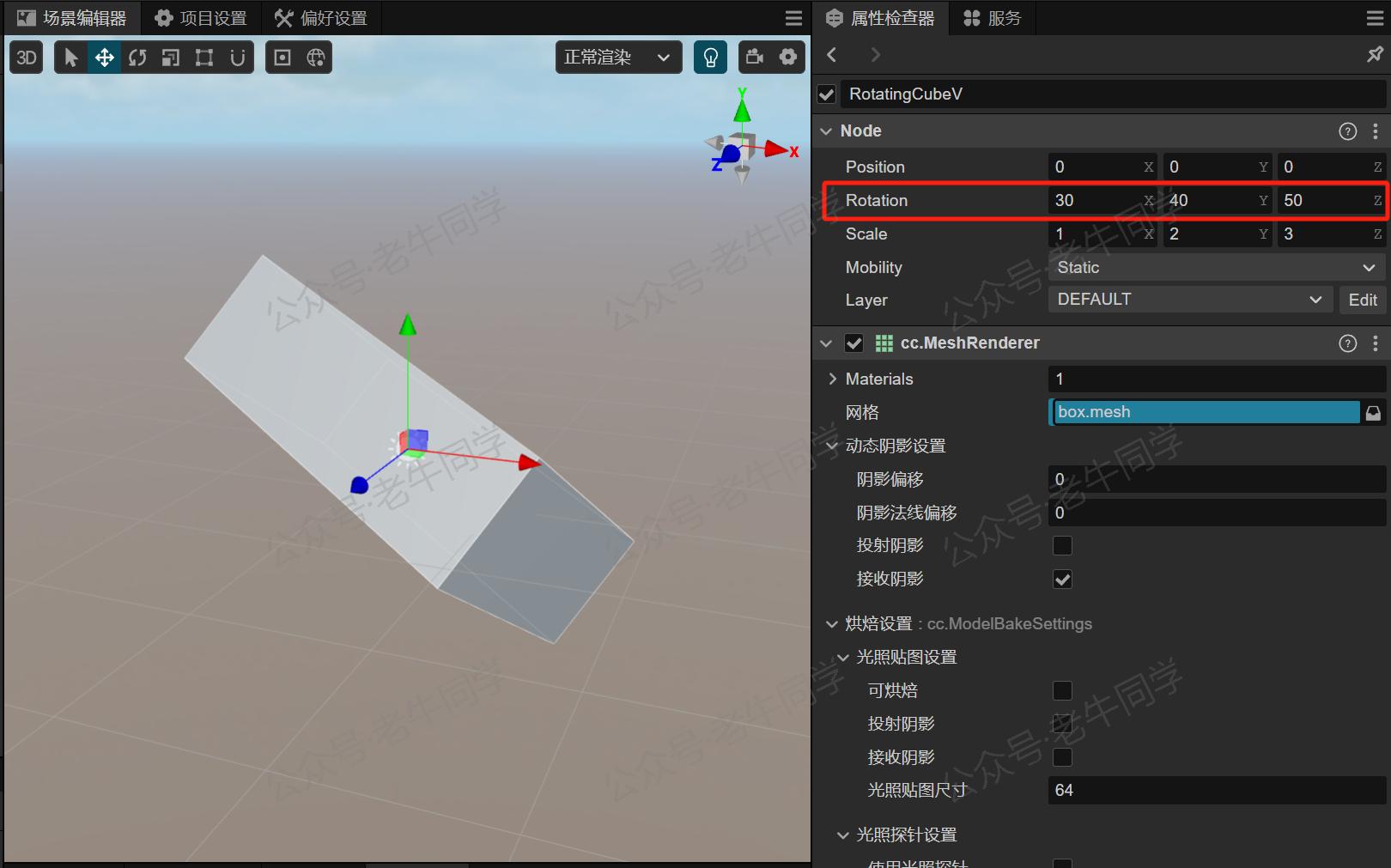
长方体旋转之后的姿态

注意的是，在三维空间中，我们一般用姿态或位姿来表示物体的当前旋转，它有两层含义：

物体方向，或者朝向
物体局部坐标系相当于世界坐标系的偏移量

四元数由爱尔兰数学家威廉·罗文·汉密尔顿（William Rowan Hamilton）于 1843 年提出。汉密尔顿希望找到一种用于描述三维空间旋转的数系。据说，汉密尔顿有一次在散步时突然想到了四元数的基本公式，并将其刻在了一座桥上。

四元数由一个实部和三个虚部组成，形式为：Q = W + Xi + Yj + Zk，其中W,X,Y,Z是实数，i,j,k是虚数单位。

既然欧拉角表示旋转已经足够优秀了，为什么还需要引入四元数呢？

原因在于，欧拉角虽然简单直观，但存在三个问题：万向锁问题（Gimbal Lock）、旋转过程中插值困难、计算效率较低的问题。

接下来，老牛同学根据自己的理解，逐一介绍欧拉角的这几个问题，同时看看四元数是如何解决的。

什么是旋转，什么是坐标系？

在介绍欧拉角和四元数之前，先了解一下旋转和坐标系。

旋转是指物体在三维空间中绕某个轴进行角度变化的运动：

轴：在三维空间中，我们一般 X 轴、Y 轴和 Z 轴表示。
角度：通常用角度或弧度来表示。
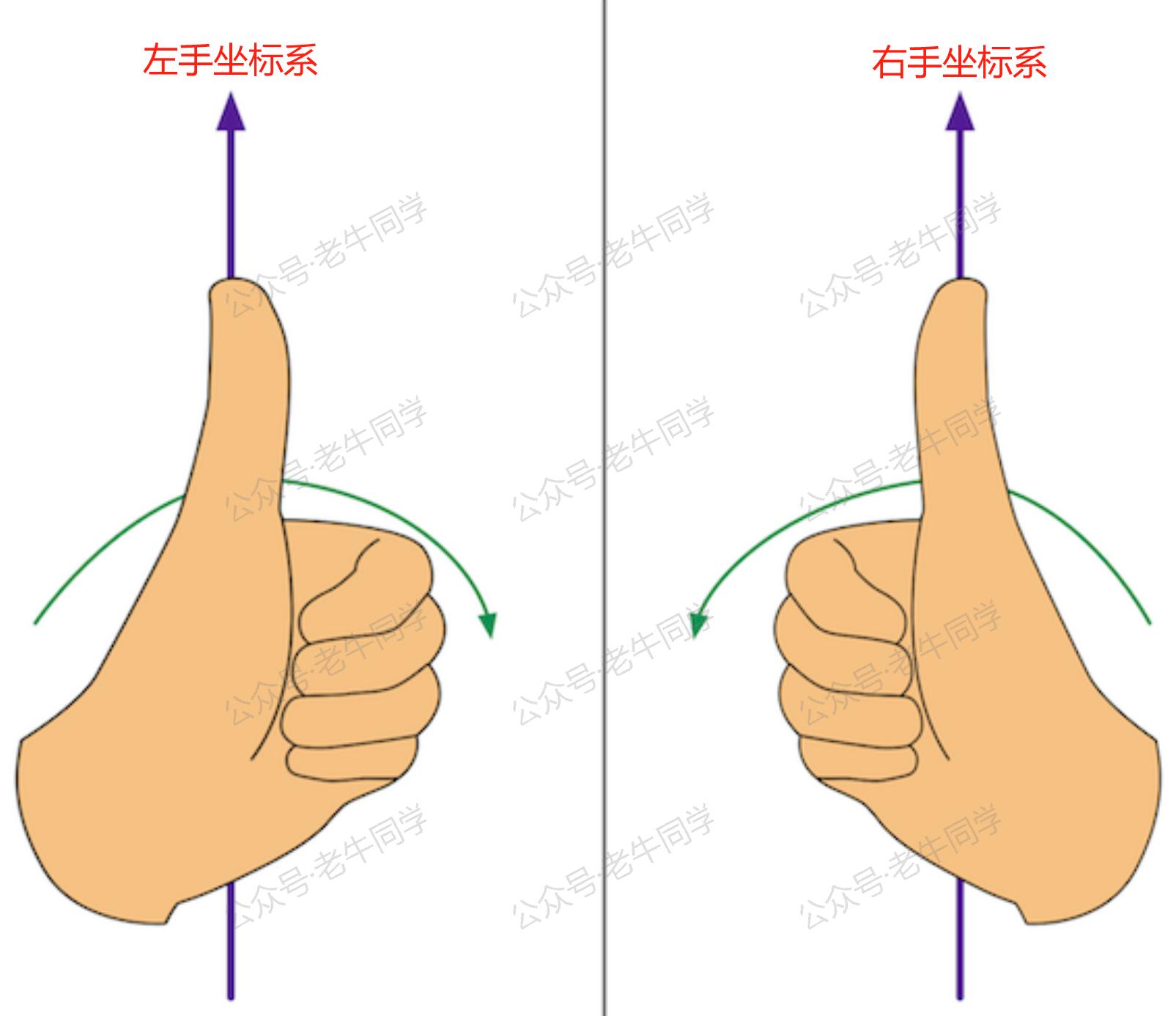
运动方向：分为右手坐标系或者左手坐标系。Cocos 3D 使用右手坐标系，Unity 3D 使用左手坐标系。默认情况下，轴默认配置：X 轴向右为正，Y 轴向上为正，Z 轴朝屏幕外为正。

右手坐标系旋转方向：伸出右手，大拇指指向轴的正方向（如：围绕 X 轴旋转+30°，则大拇指指向 X 轴的正方向）；弯曲四指，四指弯曲的方向为旋转正方向（如：+30°），反过来手背方向便是负方向。

左手坐标系旋转方向：类似于右手坐标系，伸出左手即可。

左手和右手坐标系

世界坐标系： 三维空间的参考框架，所有物体的参考标准，它是固定不变的。

本地坐标系： 每个物体都有的自己的坐标系，用于描述其自身的姿态。

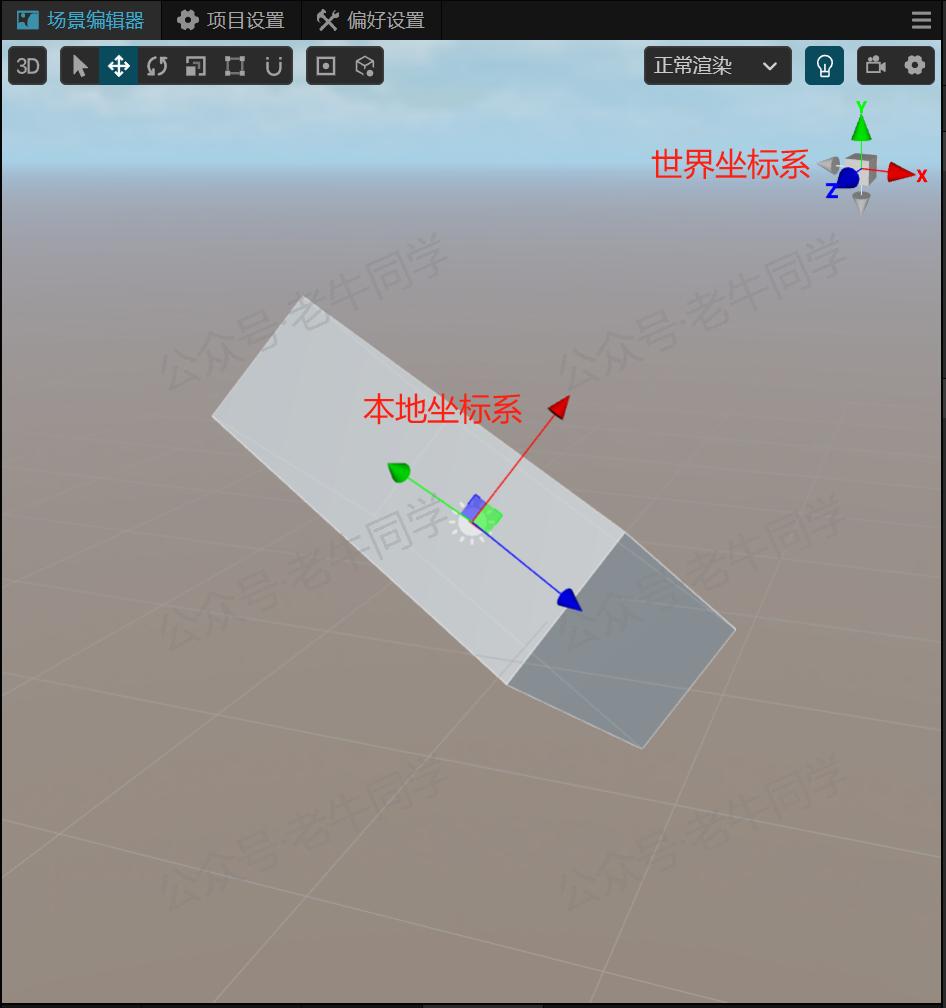
世界和局部坐标系

一般情况下，我们所说的旋转指的是局部坐标系，当然也可以相对于全局坐标系。

万向锁问题和解法

万向节常用在汽车动力传输上，它是汽车驱动系统关节，它可以围绕不同方向旋转：

万向节

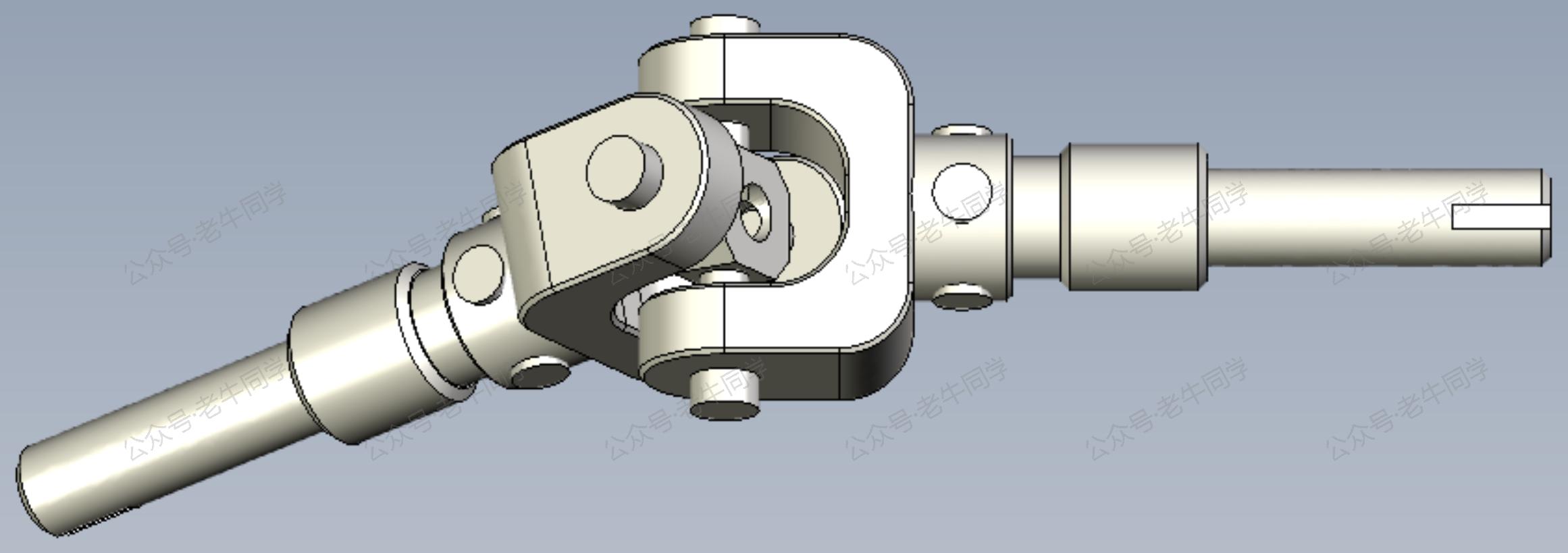
在解释万向锁问题之前，有三个非常重要的概念必须理解：

无论是欧拉角还是四元数，它们表示的是物体旋转后的姿态，是一个描述，它不是一个连续的动作。比如：欧拉角(90,0,0)代表围绕 X 轴旋转+90°，它表示的是这个物体旋转+90° 后的姿态，而不是表示物体围绕 X 轴，从 0°->1°->2°->……->90° 这个过程。因此，这里的“旋转”它不是指一个连续的动作！
物体姿态与旋转的顺序密切相关，相同的角度，不同的旋转顺序，物体的姿态是不相同的。我们可以拿个快递盒子，做个简单的实验就能明白。如：围绕 X 轴旋转 90°，Y 轴 45°，X→Y→Z旋转顺序，和Y→X→Z旋转顺序，快递盒子的姿态是不同的。
物体按照某个顺序依次旋转，前面的轴旋转时，会带动后面的轴一同旋转，而后面轴旋转却不会影响前面的轴。如：X→Y→Z 旋转顺序，当围绕 X 轴旋转时，本地坐标系 Y 轴和 Z 轴一同旋转；当围绕 Y 轴旋转时，Z 轴会一同旋转，但 X 轴是不动的；最后，当围绕 Z 轴旋转时，X 轴和 Y 轴都不会动！

第 3 点感觉非常的诡异，老牛同学就被这个不可思议的概念折磨了好久，直到彻底理解了第 1 点：永远记住，欧拉角和四元数这些表示旋转的工具，它们只是描述旋转后的姿态，并不是旋转动作（旋转在这里当名称理解），它没有动作过程，只是最终的瞬时的姿态！

如果大家理解了第 1 点，那么可以退一步想：X→Y→Z 旋转顺序，如果围绕 Y 轴旋转时，X 轴也跟着旋转，那么 X 轴最初的旋转不就白费了吗？

如果第 3 点无法理解的话，那么万向锁的问题是无法理解，因为它就是万向锁产生的前提！

至此，大家也可以到网上看看数学推导公式，在此老牛同学就不列举了！

万向锁定义：当两个旋转轴重合时，原本三个独立的旋转轴（X、Y、Z）变成了两个，导致自由度减少的现象。

我们先来看看，万向锁发生的场景：物体的任意旋转顺序（如：X→Y→Z，Y→X→Z 等），当围绕第 2 个轴旋转的角度为 ±90° 时，那么第 3 个轴就会和第 1 个轴就会重合。这样当物体围绕第 1 个轴旋转或者第 3 个轴旋转，姿态都是一样的，无法区分，这种现象就是“万向锁”问题。

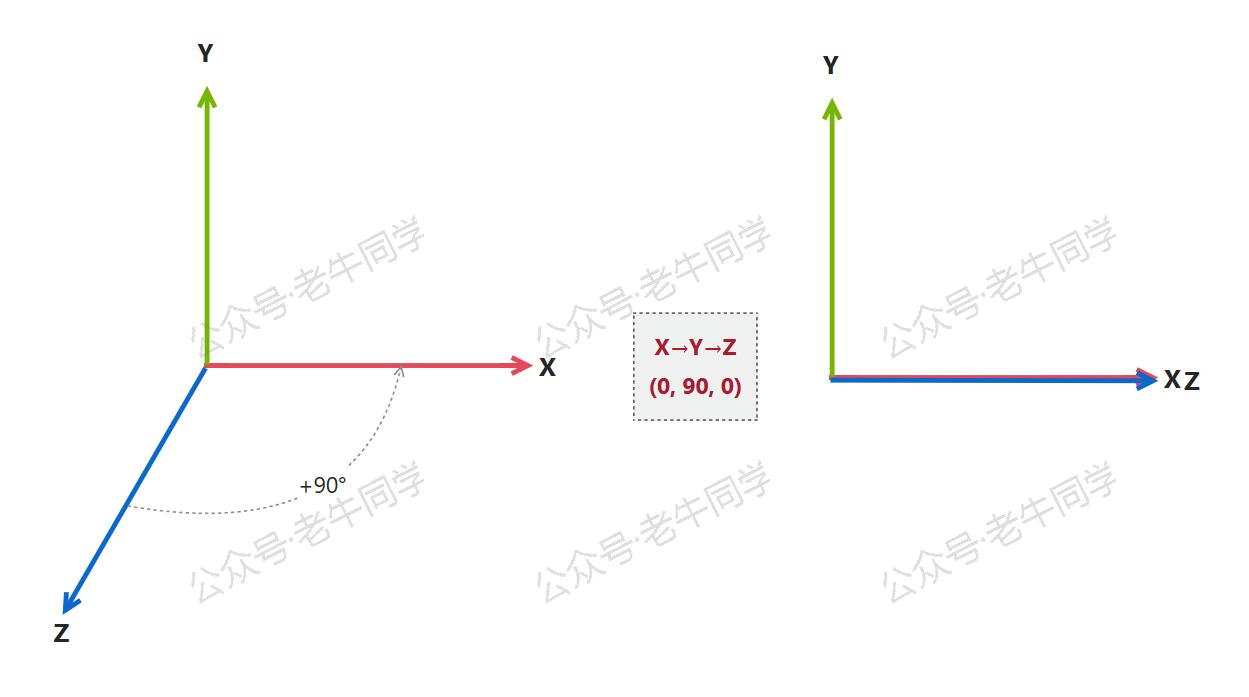
万向锁问题

如上图所示：X→Y→Z 旋转顺序，(0, 90, 0)旋转角度（X 轴和 Z 轴角度可以是任意值，此处便于理解设置为 0°），当围绕 Y 轴旋转 90° 之后，X 轴和 Z 轴重合了。这个时候，物体无论围绕 X 轴还是 Z 轴旋转，姿态都是一样的。

那么，四元数是如何解决欧拉角万向锁问题的呢：由上述公式可以看出，它没有旋转轴的概念，而是由四个数值表示旋转，表示方式为cos(θ/2)+sin(θ/2)(xi+yj+zk)；其中，θ 代表旋转的角度，(x,y,z)代表旋转轴方向。

插值和计算效率问题

插值问题的理解：插值是指物体旋转路径上的中间状态（即平滑过渡），欧拉角使用三个角度描述旋转，容易出现冗余或等效旋转的问题（如：(0, 0, 0)和(360, 360, 360)），导致旋转路径不自然，当发生万向锁问题的时候，就会发生异常。而四元数，它支持球面线性插值方法，能够生成平滑且自然的、稳定的旋转。

// 插值比例
const t = 0.5;// 1. 欧拉角线性插值
const startEuler = new Vec3(0, 0, 0);
const endEuler = new Vec3(90, 45, 0);const interpolatedEuler = new Vec3(startEuler.x + (endEuler.x - startEuler.x) * t,startEuler.y + (endEuler.y - startEuler.y) * t,startEuler.z + (endEuler.z - startEuler.z) * t
);console.log(`欧拉角线性插值: ${interpolatedEuler}`);// 2. 四元数球面线性插值
const startQuat = new Quat();
const endQuat = new Quat();Quat.fromEuler(startQuat, 0, 0, 0);
Quat.fromEuler(endQuat, 90, 45, 0);const interpolatedQuat = new Quat();
Quat.slerp(interpolatedQuat, startQuat, endQuat, t);console.log(`四元数球面线性插值: (${interpolatedQuat.w}, ${interpolatedQuat.x}, ${interpolatedQuat.y}, ${interpolatedQuat.z})`);

计算效率问题：主要是运算复杂度高，涉及大量的三角函数运算，计算效率比较低。而四元数，可通过简单的向量点积和叉积实现计算，计算效率较高。

欧拉角和四元数转换

在 Cocos 3D 中，欧拉角的使用简单且直观，使用Vec3对象表示：

// 1. 获取欧拉角（单位：度）
const euler: Vec3 = this.node.eulerAngles;
console.log(`X: ${euler.x}°`);
console.log(`Y: ${euler.y}°`);
console.log(`Z: ${euler.z}°`);// 2. 设置欧拉角（X/Y/Z，单位：度）
this.node.eulerAngles = new Vec3(45, 30, 15);

四元数使用Quat对象表示：

// 3. 获取四元数
const quat1: Quat = this.node.getRotation();
console.log(`四元数 w: ${quat1.w}, x: ${quat1.x}, y: ${quat1.y}, z: ${quat1.z}`);// 4. 设置四元数（w, x, y, z）
const quat2 = new Quat(0.707, 0, 0, 0.707);
this.node.setRotation(quat2);

欧拉角和四元数，也可以相互转换：

// 5. 欧拉角转四元数
const quat3 = new Quat();
Quat.fromEuler(quat3, euler.x, euler.y, euler.z);
console.log(`欧拉角转四元数 w: ${quat3.w}, x: ${quat3.x}, y: ${quat3.y}, z: ${quat3.z}`);// 6. 四元数转欧拉角
Quat.toEuler(euler, quat2);
console.log(`四元数转欧拉角: X=${euler.x}°, Y=${euler.y}°, Z=${euler.z}°`);

实战：垂直地面旋转立方体

接下来，我们来一个应用实战：旋转立方体，让对角线垂直于地面，然后围绕对角线不停地旋转！

旋转的立方体

让立方体的对角线垂直于地面，用欧拉角很难表示。从代码中可以看到，用四元数可以轻松实现。

首先，让立方体的对角线垂直于地面立起来：

/*** 初始化：立起来*/
protected start(): void {// 立方体对角线顶点向量const scale: number = this.node.scale.x;const localDiagonal = new Vec3(scale, scale, scale);// 归一化Vec3.normalize(localDiagonal, localDiagonal);// 本地对角线旋转到Y轴的旋转const targetDirection = new Vec3(0, 1, 0);const rotation = new Quat();Quat.rotationTo(rotation, localDiagonal, targetDirection);// 应用旋转，立起来this.node.setRotation(rotation);
}

然后，让立方体按照指定的弧度参数，沿着世界坐标系 Y 轴进行旋转（因为第一次旋转之后，立方体的本地坐标系已经发生了变化，但是世界坐标系是固定不变）：

    /*** 帧更新：旋转*/protected update(dt: number): void {const rotation = new Quat();Quat.fromAxisAngle(rotation, Vec3.UNIT_Y, this.rotateSpeed);this.node.rotate(rotation, Node.NodeSpace.WORLD);}