相关与卷积
一维相关和卷积运算是两个向量共同作用得到一个新的向量。
相关的分量形式:
\[\begin{aligned}
映射(f: \mathbb{Z} \to \mathbb{R}),对于(w = (w(-a), \ldots, w(0), \ldots, w(a))),
\\
一维相关: g(x) = \sum_{s = -a}^{a} w(s)f(x + s), x \in \mathbb{Z}.
\end{aligned}
\]
卷积的分量形式:
\[\begin{aligned}
映射(f: \mathbb{Z} \to \mathbb{R}),对于(w = (w(-a), \ldots, w(0), \ldots, w(a))),
\\
一维卷积(f \star w : \mathbb{Z} \to \mathbb{R}): g(x) := (f \star w)(x) = \sum_{s = -a}^{a} w(- s)f(x + s), x \in \mathbb{Z}.
\end{aligned}
\]
卷积是一种线性变换。
对于长度为M的卷积核\(w = h[0]...h[M - 1]\),卷积\(g(x) := (f \star w)(x)\) 等价于对向量\(x\)左乘了一个矩阵H。其中H是一个循环矩阵(也就是toeplitz矩阵).
\[H =
\begin{bmatrix}
h[0] & 0 & \cdots & 0 \\
h[1] & h[0] & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
h[M - 1] & h[M - 2] & \cdots & h[0] \\
0 & h[M - 1] & \cdots & h[1] \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & h[M - 1]
\end{bmatrix}
\]
二维卷积示例:
这里卷积核为
\[\begin{bmatrix}
0 & 2 & 0\\
1 & 2 & 1\\
2 & 0 & 2\\
\end{bmatrix}
\]

二维卷积和相关和一维情况类似,都是左乘一个卷积核形成的一个循环矩阵。一般在机器学习里面卷积和相关相同,因为一般用到的卷积核是对称的。
傅里叶变换(FT)
相关概念:数学分析中的傅里叶展开/数值分析里的最佳平方逼近。
即选择一簇线性无关的函数基(三角函数是正交的,自然线性无关)逼近要拟合的函数。
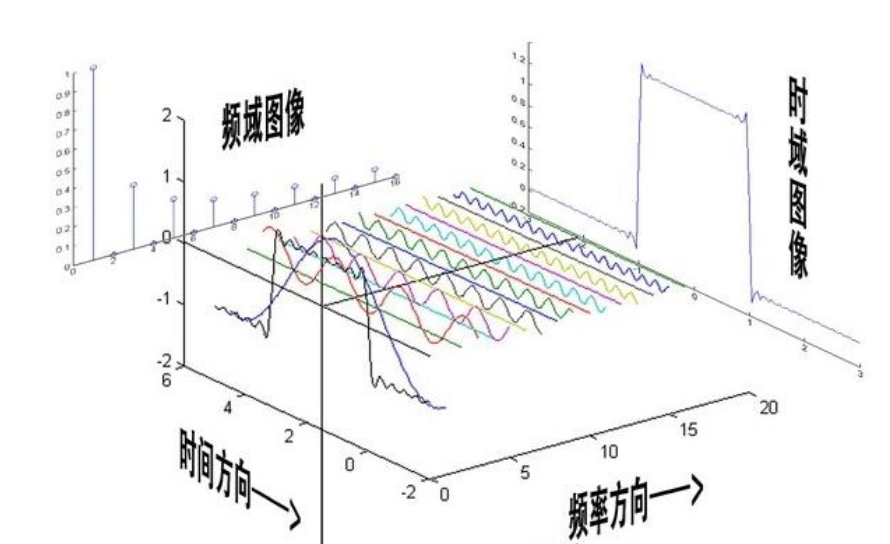
卷积,toeplitz矩阵与FT的关系
通过上述分析可以知道,卷积对应的线性变换的矩阵表示就是toeplitz矩阵,对一个向量做卷积就是左乘一个toeplitz矩阵。同时根据傅里叶变换中的性质,有在时间域的卷积操作等价于是频率域中的乘积。所以左乘一个toeplitz矩阵可以通过傅里叶变换来进行计算。
也就是$$g=f\star h=fft^{-1}(fft(f)fft(h))=Ah$$