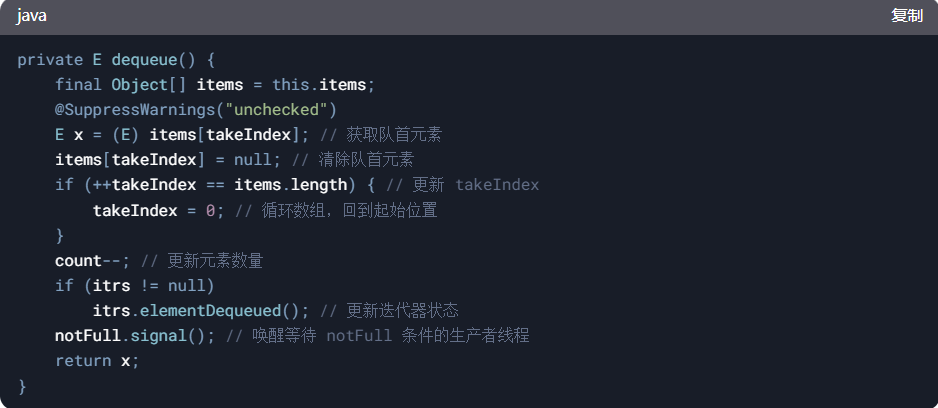
A. Was there an Array?
题意:一个长度为\(n\)的\(a\)数组,变成了长度为\(n-2\)的\(b\)数组,对于每个\(i \in [2, n - 1]\),如果\(a_i == a_{i-1} \&\& a_i == a_{i+1}\)则\(b_{i-1} = 1\),否则等于\(0\)。现在给你一个\(b\)数组,判断有没有一个\(a\)数组可以变成\(b\)。
如果\(b\)中有\(1,0,1\)这个子数组,那么一定没有对应的\(a\)数组,因为\(a_{i-1} = a_{i} = a_{i + 1}, a_{i+1} = a_{i+2} = a_{i+3}\)可以得出这几个都相等,但中间有个零,告诉你有三个数不都相同,产生矛盾。否则一定可以,因为两个\(1\)之间有两个以上的零是可以构造方案的,其他情况也是合法的。
点击查看代码
void solve() {int n;std::cin >> n;std::vector<int> a(n - 2);for (int i = 0; i < n - 2; ++ i) {std::cin >> a[i];}for (int i = 0; i + 2 < n - 2; ++ i) {if (a[i] == 1 && a[i + 1] == 0 && a[i + 2] == 1) {std::cout << "NO\n";return;}}std::cout << "YES\n";
}
B. Set of Strangers
题意:给你一个矩阵,你每次可以选择一些元素,使得它们的值都相同且没有两个元素相邻,然后把他们变成另一种元素,问让整个矩阵相同的最小操作数。
发现同一种颜色最多操作两次,如果这个颜色每个元素都不相邻,那么只需要一次就可以全部变,如果有相邻点,那么可以取\(i + j\)是偶数的位置一组,和\(i + j\)是奇数的位置一组,这两类的每一类中的元素一定不相邻,所有最多两次操作。
于是把每个元素的操作数存下来,排序后除最后一个不选,其他颜色的操作数都算上。
点击查看代码
void solve() {int n, m;std::cin >> n >> m;std::vector a(n, std::vector<int>(m));for (int i = 0; i < n; ++ i) {for (int j = 0; j < m; ++ j) {std::cin >> a[i][j];-- a[i][j];}}const int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};std::vector<int> cnt(n * m);for (int i = 0; i < n; ++ i) {for (int j = 0; j < m; ++ j) {if (cnt[a[i][j]] < 2) {cnt[a[i][j]] = 1;for (int k = 0; k < 4; ++ k) {int x = i + dx[k], y = j + dy[k];if (x < 0 || x >= n || y < 0 || y >= m) {continue;}if (a[i][j] == a[x][y]) {cnt[a[i][j]] = 2;}}}}}std::vector<int> b;for (int i = 0; i < n * m; ++ i) {if (cnt[i]) {b.push_back(cnt[i]);}}std::sort(b.begin(), b.end());int ans = 0;for (int i = 0; i + 1 < b.size(); ++ i) {ans += b[i];}std::cout << ans << "\n";
}
C. Beautiful Sequence
题意:给你一个数组,只有\(1, 2, 3\)三种值,你要选以\(1\)开头,\(3\)结尾,中间若干个\(2\)的子序列,求有多少个。
预处理\(pre1, suf2, suf3\),,表示\(1\)的个数的前缀和,\(2\)的个数的后缀和,\(3\)的个数的后缀和。然后枚举每个\(2\),只选这个\(2\)在中间就有\(pre1_i \times suf3_i\)种选法,然后考虑在前面选若干个\(2\),设\(j < i, a_j == 2\),前面每个\(2\)在\(1\)的后面的选法有\(pre1_j\)个,但两个\(2\)中间有一些\(2\)这些\(2\)可选可不选,一共\(2^{suf2_j - suf2_i - 1}\)种选法,但发现不好处理,可以直接算是\(2^{suf2_j - 1}\)个,那么前面总共是\(\sum_j pre1_j \times 2^{suf2_j - 1} \times suf3_i\)的贡献,考虑消除重复的贡献,直接都除上\(2^{suf2_i}\)就行了,\(\frac{\sum_j pre1_j \times 2^{suf2_j - 1} \times suf3_i}{2^{suf2_i}} = \sum_{j} pre1_j \times 2^{suf2_j - suf2_i - 1} \times suf3_i\),正好是我们所求的。
点击查看代码
void solve() {int n;std::cin >> n;std::vector<int> a(n);for (int i = 0; i < n; ++ i) {std::cin >> a[i];}std::vector<int> pre1(n + 1), suf2(n + 2), suf3(n + 2);for (int i = 0; i < n; ++ i) {pre1[i + 1] = pre1[i] + (a[i] == 1);}for (int i = n - 1; i >= 0; -- i) {suf2[i + 1] = suf2[i + 2] + (a[i] == 2);suf3[i + 1] = suf3[i + 2] + (a[i] == 3);}Z ans = 0, pre = 0;for (int i = 1; i <= n; ++ i) {if (a[i - 1] == 2) {ans += (Z)pre1[i] * suf3[i] + pre / power<Z>(2, suf2[i]) * suf3[i];pre += pre1[i] * power<Z>(2, suf2[i] - 1);}}std::cout << ans << "\n";
}
D. Palindrome Shuffle
题意:给你一个字符串,你可以进行一次操作,重新排列一个区间,使得字符串是回文串,求区间最短长度。
记\(l\)为\(s[1, l - 1] != s[n - l + 1, n]\)的最小的位置,\(r\)为\(s[r, n / 2] != s[n / 2 + 1, n - r + 1]\)的最大的位置,那么看\(s[l ... r]\)和\(s[n - r + 1 ... n - l + 1]\)的字符数是不是相等,如果相等,则可以重排\(s[l .. r]\)使得字符串是回文串。
否则我们可以二分往中间左边走几步和往中间右边走几步,看重排这个区间能否是回文串,\(check\)就是先判断对称的另一边没被选择的位置上的字符在这个区间是不是足够,然后剩下的一定要是偶数,因为要左边一个右边一个。
点击查看代码
void solve() {std::string s;std::cin >> s;int n = s.size();std::vector<std::array<int, 26>> sum(n + 1);for (int i = 0; i < n; ++ i) {sum[i + 1] = sum[i];sum[i + 1][s[i] - 'a'] += 1;}int l = 0;while (l < n / 2 && s[l] == s[n - 1 - l]) {++ l;}if (l == n / 2) {std::cout << 0 << "\n";return;}int r = n / 2 - 1;while (r > l && s[r] == s[n - 1 - r]) {-- r;}bool flag = true;++ l, ++ r;for (int i = 0; i < 26; ++ i) {if (sum[r][i] - sum[l - 1][i] != sum[n - l + 1][i] - sum[n - r][i]) {flag = false;break;}}if (flag) {std::cout << r - l + 1 << "\n";} else {auto check1 = [&](int k) -> bool {std::array<int, 26> cnt{};for (int i = 0; i < 26; ++ i) {cnt[i] = sum[n / 2 + k][i] - sum[l - 1][i];}for (int i = (n - l + 1); i > n / 2 + k; -- i) {if ( -- cnt[s[i - 1] - 'a'] < 0) {return false;}}for (int i = 0; i < 26; ++ i) {if (cnt[i] & 1) {return false;}}return true;};int L = 1, R = (n - l + 1) - n / 2;while (L < R) {int mid = L + R >> 1;if (check1(mid)) {R = mid;} else {L = mid + 1;}}int ans = L + n / 2 - l + 1;auto check2 = [&](int k) -> bool {std::array<int, 26> cnt{};for (int i = 0; i < 26; ++ i) {cnt[i] = sum[n - l + 1][i] - sum[n / 2 - k][i];}for (int i = l; i < n / 2 - k + 1; ++ i) {if ( -- cnt[s[i - 1] - 'a'] < 0) {return false;}}for (int i = 0; i < 26; ++ i) {if (cnt[i] & 1) {return false;}}return true;};L = 1, R = n / 2 - l + 1;while (L < R) {int mid = L + R >> 1;if (check2(mid)) {R = mid;} else {L = mid + 1;}}ans = std::min(ans, L + (n - l + 1) - n / 2);std::cout << ans << "\n";}
}