目录
- 题目
- 题解:dfs
题目
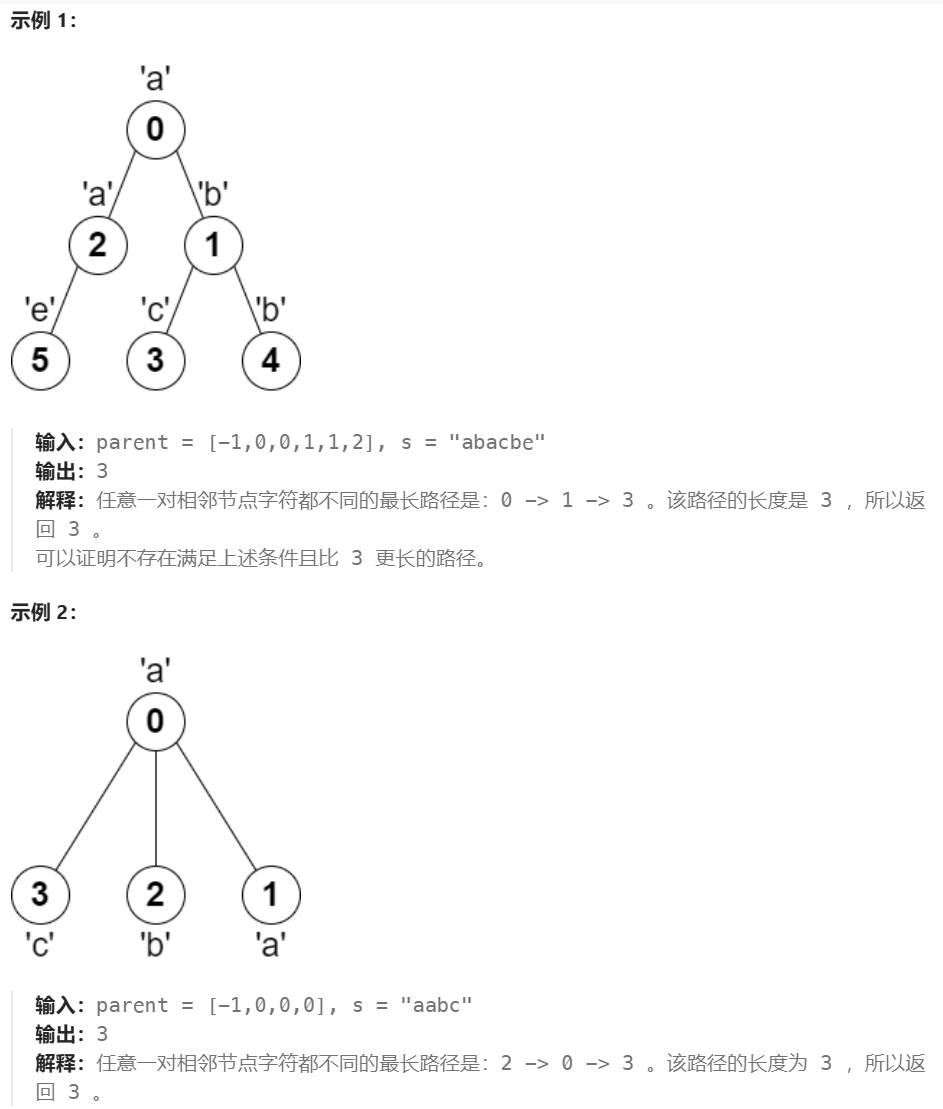
- 给你一棵 树(即一个连通、无向、无环图),根节点是节点 0 ,这棵树由编号从 0 到 n - 1 的 n 个节点组成。用下标从 0 开始、长度为 n 的数组 parent 来表示这棵树,其中 parent[i] 是节点 i 的父 节点,由于节点 0 是根节点,所以 parent[0] == -1 。
另给你一个字符串 s ,长度也是 n ,其中 s[i] 表示分配给节点 i 的字符。
请你找出路径上任意一对相邻节点都没有分配到相同字符的 最长路径 ,并返回该路径的长度。
题解:dfs
- 根据数组存储孩子节点,先求孩子的最长路径,再求当前节点的最长路径,在递归过程中更新最长路径
var longestPath = function(parent, s) {const n = parent.length; // 获取节点数量const heir = new Array(n).fill(0).map(() => []); // 创建邻接表以存储每个节点的子节点let ans = 0; // 变量用于存储最长路径的长度// 构建树的结构for (let i = 1; i < n; i++) {heir[parent[i]].push(i); // 将每个节点的索引添加到其父节点的子节点列表中}// 深度优先搜索函数const dfs = (i) => {let maxLen = 0; // 当前节点的最长路径长度初始化为0// 遍历当前节点的所有子节点for (let j of heir[i]) {let len = dfs(j) + 1; // 递归计算子节点的最长路径并加上当前边的长度// 检查当前节点与子节点的字符是否不同if (s[i] !== s[j]) {// 更新全局最长路径ans = Math.max(ans, maxLen + len);// 更新当前节点的最长路径maxLen = Math.max(len, maxLen);}}// 返回从当前节点出发的最长路径长度return maxLen;}dfs(0); // 从根节点开始DFSreturn ans + 1; // 返回最长路径长度,+1是因为路径长度是边的数量
};