Description
有 \(n\) 个点排成一行,第 \(i\) 个点与第 \(i+1\) 个点之间的距离为 \(w_i\) 个单位。
每个点都有一个加油站,第 \(i\) 个点的加油站可以给你的车加能跑 \(g_i\) 个单位的油。
若一辆初始没有油的车能从 \(l\) 一路向右开到 \(r\),也能从 \(r\) 一路向左开到 \(l\),则称 \(l,r\) 之间可以往返。
另外,你有 \(k\) 次将某个 \(g_i\) 加 \(1\) 的机会。请你求出在 \(l,r\) 之间可以往返的情况下,\(r−l+1\) 的最大值。
\(n\leq 10^5\),\(k,w_i,g_i\leq 10^9\)。
Solution
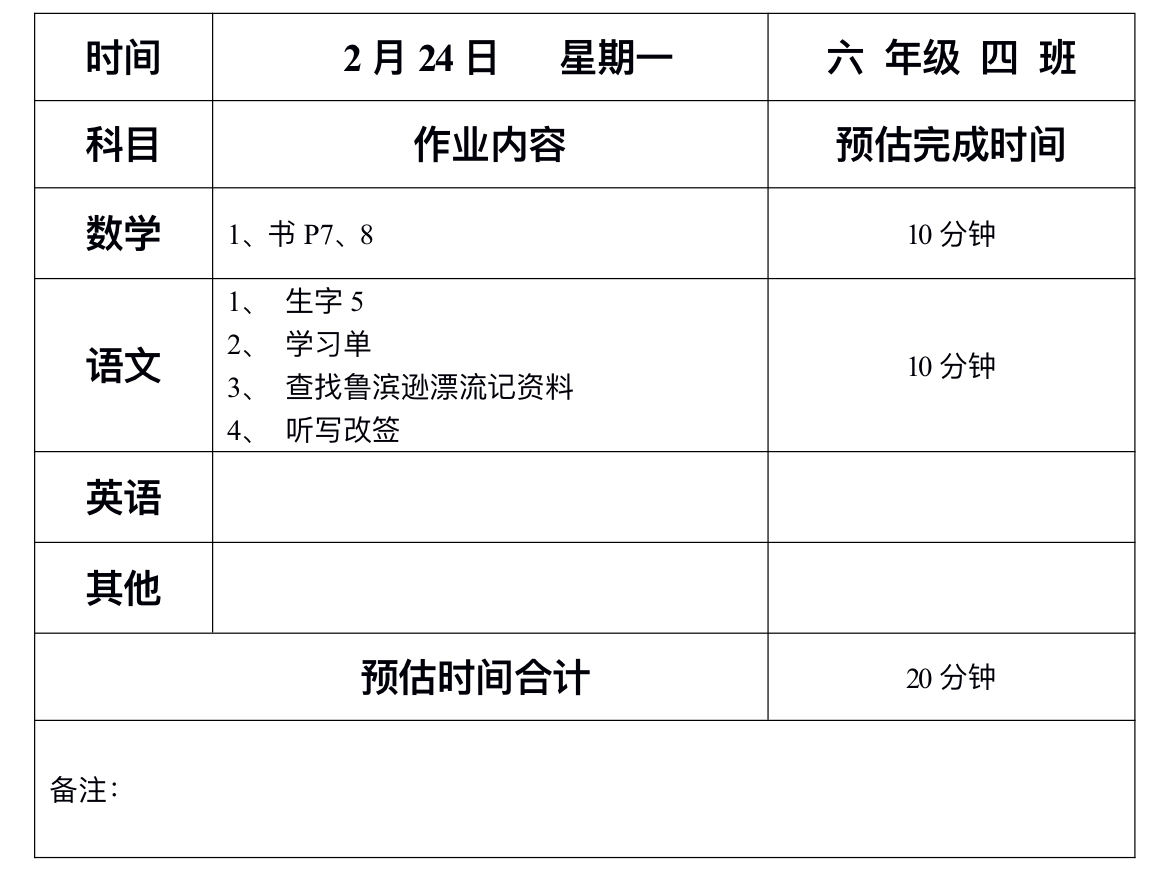
首先考虑对于 \([l,r]\),什么样的 \(g\) 和 \(w\) 能满足条件。容易发现需要满足:
和
设 \(a_k=\sum_{i=1}^{k}{(w_{i-1}-g_{i-1})}\),\(b_k=\sum_{i=1}^{k}{(g_i-w_{i-1})}\),则需要满足 \(a_l=\max_{i=l}^{r}{a_i}\) 且 \(b_r=\max_{i=l}^{r}{b_i}\)。
那么让 \(g_i\) 加一,会让 \(a_{i+1},a_{i+2},\ldots,a_{n}\) 减一和 \(b_{i},b_{i+1},\ldots,b_{n}\) 加一。
如果只有 \(a\) 的限制,对于固定的 \(l\) 右边的第一个 \(a_x>a_l\) 的位置 \(x\),需要满足 \([l,x-1]\) 这个区间至少需要操作 \(a_x-a_l\) 次,操作过后对于 \(x\) 右边的第一个位置 \(y\),同样需要满足 \([x,y-1]\) 要操作 \(a_y-a_x\) 次。
这启发我们维护一个单调栈,然后从后往前扫 \(l\),对于栈中的元素 \(c_i\),贪心地选择在 \(g_{c_i-1}\) 操作 \(a_{c_{i-1}}-a_{c_i}\) 次。
同时通过线段树维护出操作后的 \(b\) 数组,题目转化为:区间加,查询最大的 \(r\) 满足 \(\max_{i=l}^{r}{b'_i}-b'_r\leq k'\)。
注意到 \(b'_r=b_r+cnt_{<r}\) 而 \(k'=k-cnt_{<r}\),所以转化为查询最大的 \(r\) 满足 \(\max_{i=l}^{r}{b'_i}-b_r\leq k\)。
由于这里 \(\max_{i=l}^{r}b'_i\) 包含 \(b'_r\),不利于二分,所以可以先二分出 \(b'_r-b_r\leq k\) 的一个边界 \(r_{max}\),然后变为查询 \([l,r_{max}]\) 内 \(\max_{i=l}^{\color{red}{r-1}}{b'_i}-b_r\leq k\) 的最大 \(r\)。
先把区间外的位置加上一个极大值,变成全局查询 \(\max_{i=1}^{r-1}b'_i-b_r\leq k\) 的最大 \(r\)。
在线段树上维护区间 \(b_i\) 最大值和 \(b'_i\) 的最大值,以及 \(mxd\) 表示只考虑当前的节点区间 \([l,r]\),右子树里 \(b_i-\max_{j=l}^{i-1}{b'_j}\) 的最大值。\(mxd\) 可以在 pushup 的时候维护。
设当前查询区间为 \([L,R]\),区间前面 \(b'_i\) 的最大值是 \(mx\)。如果 \(mxb_{ls}\leq mx\),说明左子树被 \(mx\) 完全覆盖,所以只需要二分找到左子树里 \(b_i\geq mx-k\) 的最大 \(i\),同时递归右子树。
如果 \(mxb_{ls}<mx\),说明 \(mx\) 不会影响当前区间的右子树,通过 \(mxd\) 的值判断是递归左子树还是右子树即可。
pushup 的过程同理。
时间复杂度:\(O(n\log^2 n)\)。
Code
#include <bits/stdc++.h>#define int int64_tconst int kMaxN = 1e5 + 5;int n, k;
int w[kMaxN], g[kMaxN], a[kMaxN], b[kMaxN];struct BIT {int c[kMaxN];void upd(int x, int v) {for (; x <= n; x += x & -x) c[x] += v;}int qry(int x) {int ret = 0;for (; x; x -= x & -x) ret += c[x];return ret;}
} bit;struct SGT {// int _b[kMaxN];// void build() {// for (int i = 1; i <= n; ++i) _b[i] = b[i];// }// void update(int x, int l, int r, int ql, int qr, int v) {// for (int i = ql; i <= qr; ++i) _b[i] += v;// }// int query(int mxr = n) {// // for (int i = 1; i <= n; ++i) std::cerr << _b[i] << ' ';// // std::cerr << '\n';// int ret = 0, mx = -1e18;// for (int i = 1; i <= mxr; ++i) {// if (mx - b[i] <= k) ret = i;// mx = std::max(mx, _b[i]);// }// return ret;// }int mxb[kMaxN * 4], mx_b[kMaxN * 4], tag[kMaxN * 4], mxd[kMaxN * 4];void addtag(int x, int l, int r, int v) {mx_b[x] += v, tag[x] += v, mxd[x] -= v;}void pushdown(int x, int l, int r) {if (tag[x]) {int mid = (l + r) >> 1;addtag(x << 1, l, mid, tag[x]), addtag(x << 1 | 1, mid + 1, r, tag[x]);tag[x] = 0;}}int getpos(int x, int l, int r, int v) {if (mxb[x] < v) return 0;if (l == r) return l;int mid = (l + r) >> 1;if (mxb[x << 1 | 1] >= v) return getpos(x << 1 | 1, mid + 1, r, v);else return getpos(x << 1, l, mid, v);}int getmxd(int x, int l, int r, int mx = -1e18) {if (l == r) return b[l] - mx;pushdown(x, l, r);int mid = (l + r) >> 1;// return std::max(query(x << 1, l, mid, mx), query(x << 1 | 1, mid + 1, r, std::max(mx, mx_b[x << 1])));if (mx >= mx_b[x << 1]) {return std::max(mxb[x << 1] - mx, getmxd(x << 1 | 1, mid + 1, r, mx));} else {return std::max(mxd[x], getmxd(x << 1, l, mid, mx));}}void pushup(int x, int l, int r) {mxb[x] = std::max(mxb[x << 1], mxb[x << 1 | 1]);mx_b[x] = std::max(mx_b[x << 1], mx_b[x << 1 | 1]);if (l != r) {int mid = (l + r) >> 1;mxd[x] = getmxd(x << 1 | 1, mid + 1, r, mx_b[x << 1]);}}void build(int x, int l, int r) {if (l == r) return void(mxb[x] = mx_b[x] = b[l]);int mid = (l + r) >> 1;build(x << 1, l, mid), build(x << 1 | 1, mid + 1, r);pushup(x, l, r);}void update(int x, int l, int r, int ql, int qr, int v) {if (l > qr || r < ql) return;else if (l >= ql && r <= qr) return addtag(x, l, r, v);pushdown(x, l, r);int mid = (l + r) >> 1;update(x << 1, l, mid, ql, qr, v), update(x << 1 | 1, mid + 1, r, ql, qr, v);pushup(x, l, r);}int query(int x, int l, int r, int mx) {if (l == r) return mx - b[l] <= k ? l : 0;pushdown(x, l, r);int mid = (l + r) >> 1;if (mx >= mx_b[x << 1]) {return std::max(getpos(x << 1, l, mid, mx - k), query(x << 1 | 1, mid + 1, r, mx));} else {if (mxd[x] >= -k) return query(x << 1 | 1, mid + 1, r, mx_b[x << 1]);else return query(x << 1, l, mid, mx);}}
} sgt;void upd(int x, int v) {sgt.update(1, 1, n, x, n, v);bit.upd(x, v);
}void solve() {static int stk[kMaxN];int top = 0;sgt.build(1, 1, n);sgt.update(1, 1, n, 1, n, -1e18);b[0] = -1e18;int ans = 0;for (int i = n; i; --i) {for (; top && a[stk[top]] <= a[i]; --top) {if (top > 1) upd(stk[top - 1] - 1, -(a[stk[top - 1]] - a[stk[top]]));}stk[++top] = i;if (top > 1) upd(stk[top - 1] - 1, a[stk[top - 1]] - a[stk[top]]);sgt.update(1, 1, n, i, i, 1e18);int L = i - 1, R = n + 1, mxr = i - 1;while (L + 1 < R) {int mid = (L + R) >> 1;if (bit.qry(mid - 1) <= k) L = mxr = mid;else R = mid;}sgt.update(1, 1, n, mxr, n, 1e18);ans = std::max(ans, sgt.query(1, 1, n, -1e18) - i + 1);sgt.update(1, 1, n, mxr, n, -1e18);}std::cout << ans << '\n';
}void dickdreamer() {std::cin >> n >> k;for (int i = 1; i < n; ++i) std::cin >> w[i];for (int i = 1; i <= n; ++i) std::cin >> g[i];for (int i = 1; i <= n; ++i) {a[i] = a[i - 1] + w[i - 1] - g[i - 1];b[i] = b[i - 1] + g[i] - w[i - 1];}solve();
}int32_t main() {
#ifdef ORZXKRfreopen("in.txt", "r", stdin);freopen("out.txt", "w", stdout);
#endifstd::ios::sync_with_stdio(0), std::cin.tie(0), std::cout.tie(0);int T = 1;// std::cin >> T;while (T--) dickdreamer();// std::cerr << 1.0 * clock() / CLOCKS_PER_SEC << "s\n";return 0;
}