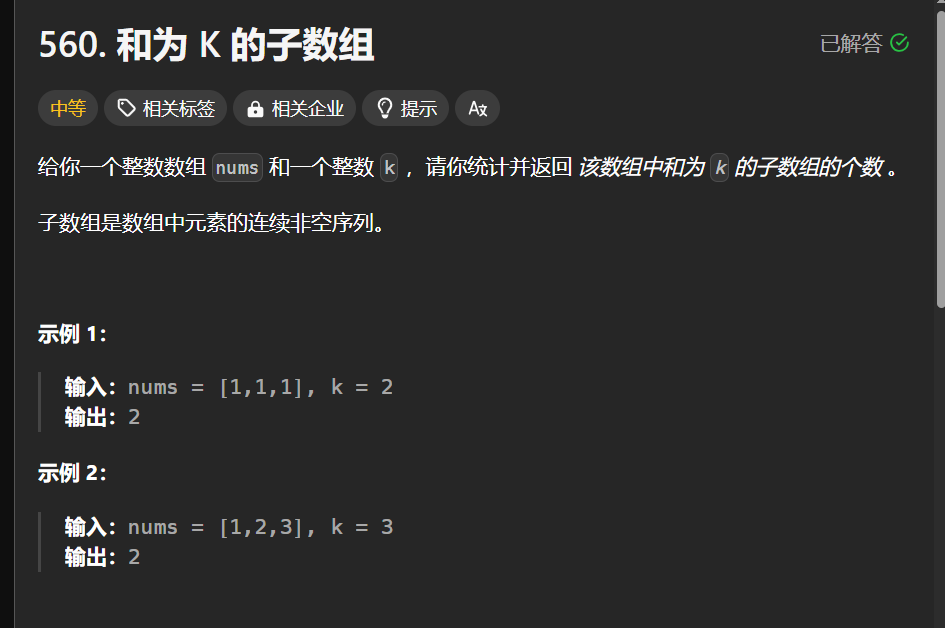
P3246 [HNOI2016] 序列
直到最后一步都是容易想到的,而最后一步恰是本题的关键所在。
首先看到 ST 表和莫队是容易想到的,那么有了莫队就应该考虑如何扩展区间。我们尝试把 \([l,r]\) 扩展到 \([l,r+1]\),发现需要知道 \(\min[l,r],\min[l+1,r],\dots,\min[r,r]\)。这个东西直接做显然是不好做的,但是由于它显然具有单调性,考虑如果我们求出了每个值作为区间最小值的区间,应该就能求出答案。
单调栈应该就有了。
但每次扩展的时候都跑一遍单调栈显然不现实,那么我们先预处理 \(\text{lf}(i)\) 和 \(\text{rf}(i)\) 分别表示 \(a_i\) 作为区间最小值的区间左端点和右端点,这个显然一正一反两遍单调栈就能 \(O(n)\) 求出。但我们还是不知道如何求解答案。考虑一个区间 \([l,r]\) 扩展到 \([l,r+1]\),\([l,r+1]\) 的最小值 \(a_p\) 能提供贡献的区间左端点为 \([l,p]\),那么它能提供的贡献显然是 \(a_p\times(p-l+1)\),考虑求剩下这部分的贡献。
下面是核心内容。考虑设一个 \(f_{l,r}\) 表示以 \(r\) 为右端点、左端点在 \([l,r]\) 区间内的答案,利用我们刚才求出的 \(\text{lf}(i)\) 可以得到转移:\(f_{l,r}=f_{l,\text{lf}(i)}+a_r\times(r-\text{lf}(r))\)。发现和 \(l\) 无关,于是自然可以去掉 \(l\) 这一维,于是我们发现这个东西是可以预处理的。所以上面所说 “剩下这部分的贡献” 就是 \(f_r-f_p\)。
于是这题就做完了。
using ll=long long;
constexpr int MAXN=1e5+5;
int n,Q,t,F,logn[MAXN],f[MAXN][21];
int lf[MAXN],rf[MAXN],stk[MAXN],top;
ll a[MAXN],sml[MAXN],smr[MAXN],ans[MAXN];
struct Ask{int l,r,id;bool operator<(const Ask&x)const{return l/t!=x.l/t?l<x.l:l/t&1?r<x.r:r>x.r;}
}q[MAXN];void ST(){for(int j=1;j<=F;j++)for(int i=1;i+(1<<j)-1<=n;i++)f[i][j]=Min(f[i][j-1],f[i+(1<<(j-1))][j-1]);
}
int amn(int l,int r){int s=logn[r-l+1];return Min(f[l][s],f[r-(1<<s)+1][s]);
}
ll gtl(int l,int r){int mn=amn(l,r);return a[mn]*(r+1-mn)+smr[l]-smr[mn];
}
ll gtr(int l,int r){int mn=amn(l,r);return a[mn]*(mn-l+1)+sml[r]-sml[mn];
}int main(){n=read(),Q=read();F=__lg(n),t=sqrt(n);a[0]=a[n+1]=-2e9,logn[0]=-1;for(int i=1;i<=n;i++){a[i]=read();logn[i]=logn[i>>1]+1;f[i][0]=i;while(top&&a[stk[top]]>=a[i]) top--;lf[i]=stk[top];sml[i]=sml[lf[i]]+a[i]*(i-lf[i]);stk[++top]=i;}stk[top=1]=n+1;for(int i=n;i;i--){while(top&&a[stk[top]]>=a[i]) top--;rf[i]=stk[top];smr[i]=smr[rf[i]]+a[i]*(rf[i]-i);stk[++top]=i;}ST();for(int i=1;i<=Q;i++) q[i]={read(),read(),i};sort(q+1,q+Q+1);ll cnt=0;for(int i=1,l=1,r=0;i<=Q;i++){while(l>q[i].l) cnt+=gtl(--l,r);while(r<q[i].r) cnt+=gtr(l,++r);while(l<q[i].l) cnt-=gtl(l++,r);while(r>q[i].r) cnt-=gtr(l,r--);ans[q[i].id]=cnt;}for(int i=1;i<=Q;i++) write(ans[i]);return fw,0;
}