洛谷2025省选模拟赛D1T1“Ball” 题解

洛谷2025省选模拟赛D1T1“Ball” 题解

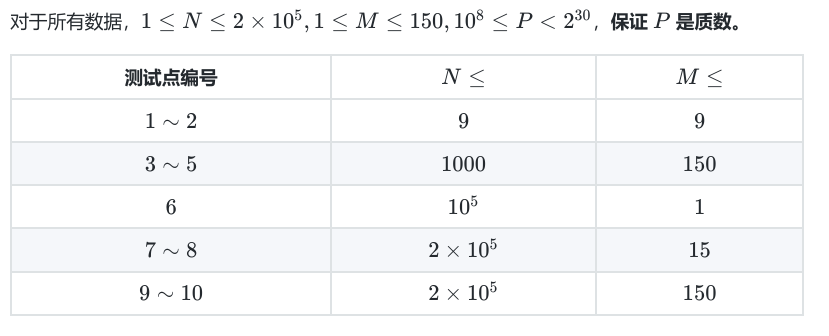
首先可以写出一个暴力的 dp ：

令 \(f_{i,j}\) 表示有 \(i\) 个选了一次的球和 \(j\) 个选了大于一次的球的期望答案，有等式：

\[f_{i,j}=\frac jnf_{i,j}+\frac{n-i-j}nf_{i+1,j}+\frac in f_{i-1,j+1} \]

进一步得 \(f_{i,j}=\frac{n-i-j}{n-j}f_{i+1,j}+\frac{i}{n-j}f_{i-1,j+1}\)

复杂度 \(\mathcal O(mn^2)\)。

发现每一次只有边界不同而转移方式相同于是套路的将过程反转，组合意义就是从”期望“变为”概率“，复杂度 \(\mathcal O(n^2+nm)\)。

发现高次方很神奇，考虑将其拆开，于是 \(E(X^i)=\sum_{j=0}^i{i\brace j}j!E{X\choose j}\)。

当看到计数里有组合数时，应该考虑用组合意义设计状态

\(E{X\choose i}\) 表示从恰好选择一次的小球中选走 \(i\) 个的方案数，令 \(g_{i,j}\) 表示现在至少拿了一次的球有 \(i\) 个，从中选走 \(j\) 个球的期望方案数。 假设选择了 \(k\) 个至少拿了一次的球，并考虑转移：

• 这次拿了一个拿过多次的球，概率 \(\frac {i-k}n\)，转移到 \(g_{i,j}\)

• 这次拿了一个拿过一次但未被选走的球，概况 \(\frac {k-j}n\)，转移到 \(g_{i,j}\)

• 这次拿了一个被选走的球，这是不合法的，因为其既然能被选走，说明最终其也是仅被拿了一次。所以概率为 \(\frac jn\)，权值为 \(0\)。

• 这次拿了一个没有拿过的球并直接选走，概率 \(\frac {n-i}n\)，转移到 \(g_{i+1,j+1}\)

• 这次拿了一个没有拿过的球但不选走，概率 \(\frac {n-i}n\)，转移到 \(g_{i+1,j}\)

整理可得：

\[g_{i,j}\times\frac{n-i}{n-i+j}\to g_{i+1,j}\\ g_{i,j}\times\frac{n-i}{n-i+j}\to g_{i+1,j+1} \]

复杂度 \(\mathcal O(nm)\)。

答案为 \(E(X^i)=\sum_{j=0}^i{i\brace j}j!g_{n,j}\)。

对于这道题就是把 "先算概率再乘组合数"的顺序换成了，通过转移一边算概率一边算组合数。

可能有小乃龙在设计 \(g\) 的时候把 \(k\) （定义见上文）也会带上，变成：

\[g_{i,j,k}\times\frac{k-j}{n-i+k}\to g_{i,j,k-1}\\ g_{i,j,k}\times\frac{n-i}{n-i+k}\to g_{i+1,j,k}\\ g_{i,j,k}\times\frac{n-i}{n-i+k}\to g_{i+1,j+1,k} \]

这是一个比较唐的行为因为明明可以直接：

把要求的那一坨设在一起，直接转移

如果真设错了并且没有意识到，我觉得难以通过数学推导手段改过来，如果真的想改我觉得也就只能：

通过设一个和式考虑整体转移

设 \(h_{i,j}=\sum_{k}g_{i,j,k}\)：

首先我们将其还原（或者说通过添加自环改变权值）

\[g_{i,j,k}\times\frac{k-j}{n}\to g_{i,j,k-1}\\ g_{i,j,k}\times\frac{i-k}{n}\to g_{i,j,k}\\ g_{i,j,k}\times\frac{n-i}{n}\to g_{i+1,j,k}\\ g_{i,j,k}\times\frac{n-i}{n}\to g_{i+1,j+1,k} \]

然后发现后两行不带 \(k\)。由于 $\to $ 是”贡献“的意思，我们可以直接替换为 \(h\)，对于左边，如果转移系数与 k 无关，我们也可以将其替换：

\[g_{i,j,k}\times\frac{k-j}{n}\to h_{i,j}\\ g_{i,j,k}\times\frac{i-k}{n}\to h_{i,j}\\ h_{i,j}\times\frac{n-i}{n}\to h_{i+1,j}\\ h_{i,j}\times\frac{n-i}{n}\to h_{i+1,j+1} \]

然后发现前两行居然转移居然起点终点都相同，那么我们可以将其合并

\[g_{i,j,k}\times\frac{i-j}{n}\to h_{i,j}\\ h_{i,j}\times\frac{n-i}{n}\to h_{i+1,j}\\ h_{i,j}\times\frac{n-i}{n}\to h_{i+1,j+1} \]

然后惊奇的发现转移系数也不带 \(k\) 了于是替换为 \(h\)：

\[h_{i,j}\times\frac{i-j}{n}\to h_{i,j}\\ h_{i,j}\times\frac{n-i}{n}\to h_{i+1,j}\\ h_{i,j}\times\frac{n-i}{n}\to h_{i+1,j+1} \]

去掉自环得：

\[h_{i,j}\times\frac{n-i}{n-i+j}\to h_{i+1,j}\\ h_{i,j}\times\frac{n-i}{n-i+j}\to h_{i+1,j+1} \]

转化成功。