[字符串算法]Manacher-编程知识

[字符串算法]Manacher

news/2025/2/27 14:29:36/文章来源:https://www.cnblogs.com/rikkkkka/p/18740897

1.前置知识

回文子串 回文的子串
最长回文子串 字符串中最长的回文子串
回文半径 设以\(i\)为中心的最大回文子串的长度为\(n\),则这个字符串第\(i\)位的回文半径为\((n+1)/2\)

2.算法流程

2.1 预处理

在处理回文子串（马拉车算法适用）的问题时，一般需要求出每一位的回文半径
经常做字符串题目的同学都知道，在处理这种问题时，最大的阻碍一般就是字符串长度的奇偶性以及边界
不难想到，我们可以在字符串的首尾分别插入一个字符来解决边界问题
也不难想到，我们可以在每一个字符的首尾都添加一个字符（包括第\(1\)个和最后一个)
由此，我们可以得到一个新字符串。
这里举一个例子，
原字符串s:ababa
进行完操作1（首尾标记）的字符串 s1: @ababa@
进行完操作2（字符插入）的字符串 s2: @#a#b#a#b#a#@
根据流程不难得出代码：

cin>>a;//原串
int len=strlen(a);
int k=0;
s[0]='$';
s[1]='#';
k++;
for(int i=0;i<=len;i++)
{s[++k]=a[i];s[++k]='#';
}
n=k;

是的是的我懂你们想要照搬但是看到我那不顺眼的++k急了
这个千万不能改，是先自增在标记！！

2.2 加速盒子（核心部分）

~~我超，盒！~~
是的是的学过扩展KMP算法的同学们应该都熟悉的乐子东西
所以接下来就让我演示一下这东西
本质上是一个分类讨论分三种情况：

2.2.1 在盒内（整体）

如图，

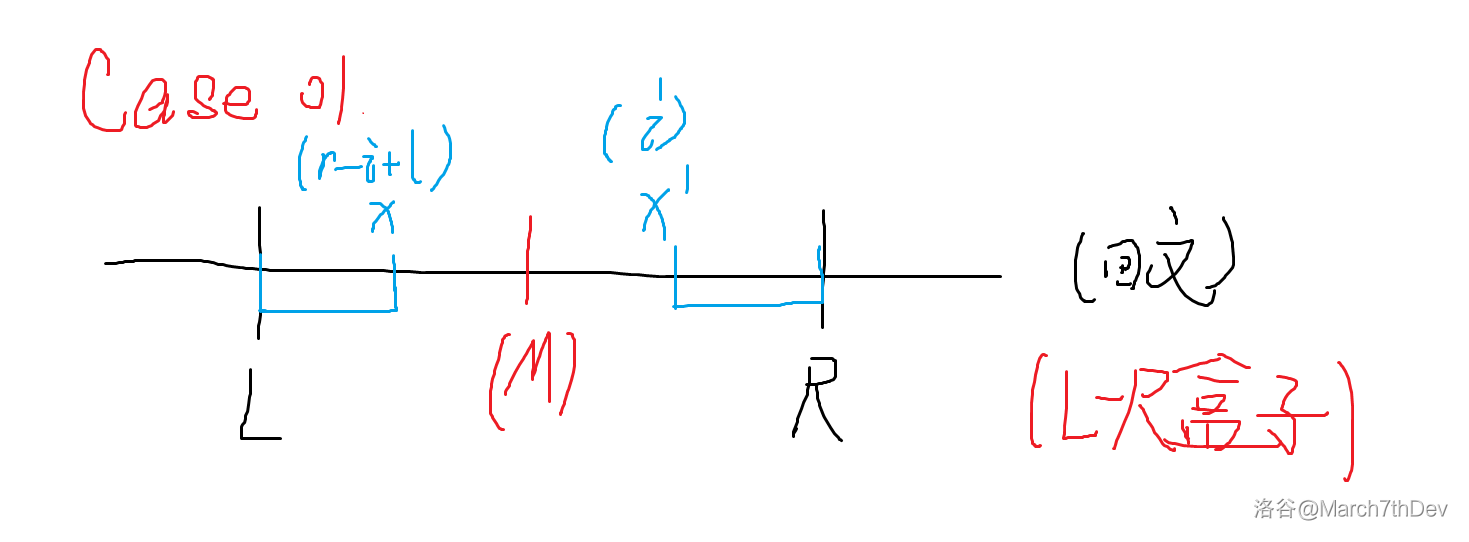
蓝色段全体在盒子内，这个时候直接用对称点的就可以了
举例：

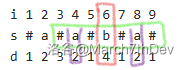
所以这是显而易见的

2.2.2 在盒内（部分）

如图，

蓝色段有一部分出去了，所以从\(r\)开始暴力

2.2.3 在盒外（全部）

不配图了，这个是显而易见的，两端都不在盒子内，因此只能暴力求解

2.2.4 更新（upd）

求出\(d[i]\)后，如果右端有最大值，那么更新盒位置

2.2.5 代码

依次逻辑则可以写出代码

int manacher(char s[],int n)
{d[1]=1;for(int i=2,l,r=1;i<=n;i++){if(l<=r){d[i]=min(d[r-i+l],r-i+1);}while(s[i-d[i]]==s[i+d[i]]){d[i]++;}if(i+d[i]-1>r){l=i-d[i]+1;r=i+d[i]-1;}}
}