#include<bits/stdc++.h>
using namespace std;
#define N 1005
struct node
{int l, r; // 左右儿子节点编号int val; // 节点值int key; // 随机key值int siz; // 子树大小int rev; // 翻转标记
} tr[N];
int n, root, idx;// 节点数,根节点编号,当前节点编号
// 构造
int newnode(int v)
{tr[++idx].val = v;tr[idx].key = rand() /*随机化key值*/;tr[idx].siz = 1;tr[idx].rev = 0;return idx;
}
// 向上更新
void pushup(int p)
{tr[p].siz = tr[tr[p].l].siz /*左侧节点数*/ + tr[tr[p].r].siz + /*右侧节点数*/ 1 /*本身*/;
}
// 向下传递懒标记
void pushdown(int p)
{// 交换左右子树swap(tr[p].l, tr[p].r);// 下传标记给子节点if (tr[p].l) tr[tr[p].l].rev ^= 1;if (tr[p].r) tr[tr[p].r].rev ^= 1;// 清除当前节点标记tr[p].rev = 0;
}// 根据val分裂
void split1(int p, int v, int &x, int &y)
{if (!p) // 当前节点为空时处理{x = y = 0;return;}if (tr[p].val <= v){x = p;split1(tr[p].r /*新当前节点*/,v /*保持阈值不变*/,tr[p].r /*将结果x挂到当前节点的右子树*/,y /*输出大于v的部分*/);}else{y = p;split1(tr[p].l /*新当前节点*/,v /*保持阈值不变*/,x /*输出小于等于v的部分*/,tr[p].l /*将结果y挂到当前节点的左子树*/);}pushup(p);
}
// 根据size分裂
// 将树p按前k个节点分裂为x(左树)和y(右树)
void split2(int p, int k, int &x, int &y)
{if (!p){x = y = 0;return;}else{pushdown(p); // 处理延迟标记// 计算左子树容量是否足够if (tr[tr[p].l].siz < k) // 左子树容量不足,需要向右子树分裂{x = p;// 递归右子树,更新剩余需要分裂的数量:k - 左子树大小 - 当前节点split2(tr[p].r, k - tr[tr[p].l].siz - 1, tr[p].r, y);}else // 左子树容量足够,向左子树分裂{y = p;// 递归左子树,保持分裂数量k不变split2(tr[p].l, k, x, tr[p].l);}pushup(p); // 更新当前节点子树大小}
}// 合并
int merge(int x, int y) // 合并两个子树(x树所有节点值 <= y树所有节点值)
{// 任意子树为空时直接返回非空子树if (!x || !y)return x + y;// 根据随机key值决定父子关系(保持堆性质)if (tr[x].key < tr[y].key) // x作为父节点{tr[x].r = merge(tr[x].r, y); // 将y合并到x的右子树pushup(x); // 更新x的子树大小return x; // 返回合并后的根节点}else // y作为父节点{tr[y].l = merge(x, tr[y].l); // 将x合并到y的左子树pushup(y); // 更新y的子树大小return y; // 返回合并后的根节点}
}
//启发式合并
int merge2(int x,int y)
{if(!x||!y)return x|y;if(tr[x].key<tr[y].key)swap(x,y);int a,b;split2(x,tr[y].siz,a,b);tr[y].l=merge2(a,tr[y].l);tr[y].r=merge2(b,tr[y].r);pushup(y);
}
//删除
void del(int v)
{int x, y, z;split1(root, v, x, z); // 把树分成小于等于v和大于v的两部分split1(x, v - 1, x, y); // 把小于等于v的部分分成小于v和等于v的两部分y = merge(tr[y].l, tr[y].r); // 把等于v的部分合并成一个节点root = merge(merge(x, y), z); // 把小于v和大于v的两部分合并成一个树
}
//插入 首先生成新节点(函数newnode)
void insert(int val)
{int x, y;// 按照val分裂成左子树x(<=val)和右子树y(>val)split1(root, val, x, y);// 将新节点合并到左子树末端,再与右子树合并形成新根root = merge(merge(x, newnode(val)), y);
}
//查找第k个 整体二分思想 看看去左边还是右边找
int getk(int p,int k)
{// 目标在左子树的情况if(k<=tr[tr[p].l].siz)return getk(tr[p].l,k);// 当前节点正好是第k个节点(左子树节点数 + 1)if(k==tr[tr[p].l].siz+1)return p;// 目标在右子树的情况,调整k值:k - 左子树大小 - 当前节点return getk(tr[p].r,k-tr[tr[p].l].siz-1);
}
//查找这东西的前驱(我也不知道这东西有什么用)
void getpre(int v)
{int x,y;split1(root,v,x,y);cout<<tr[getk(x,tr[x].siz)].val<<endl; root=merge(x,y);
}
//查找这东西的后继(我也不知道这东西有什么用*2)
void getsuc(int v)
{int x,y;split1(root,v,x,y);cout<<tr[getk(y,1)].val<<endl;root=merge(x,y);
}//对区间进行操作
void modify(int l,int r)
{/*总体:分割 对节点操作 合上*/int x,y,z;split2(root,l-1,x,y);split2(y,r-l+1,y,z);//你想进行的操作 例如翻转,求和等等//这里用反转当例子tr[y].rev^=1;root=merge(merge(x,y),z);return;
}[板子]无旋式treap
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/890649.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
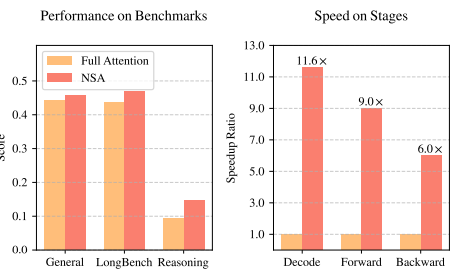
LLM大模型:deepseek浅度解析(四):Native Sparse Attention NSA原理
deepseek又整活了啊,2025.2.16的时候又发布了 "Native Sparse Attention: Hardware-Aligned and Natively Trainable Sparse Attention",核心是解决attention计算耗时耗算力的问题!NSA具体又是怎么做的了?回忆一下:attention效果好的核心原因,就是Q*K得到了tok…
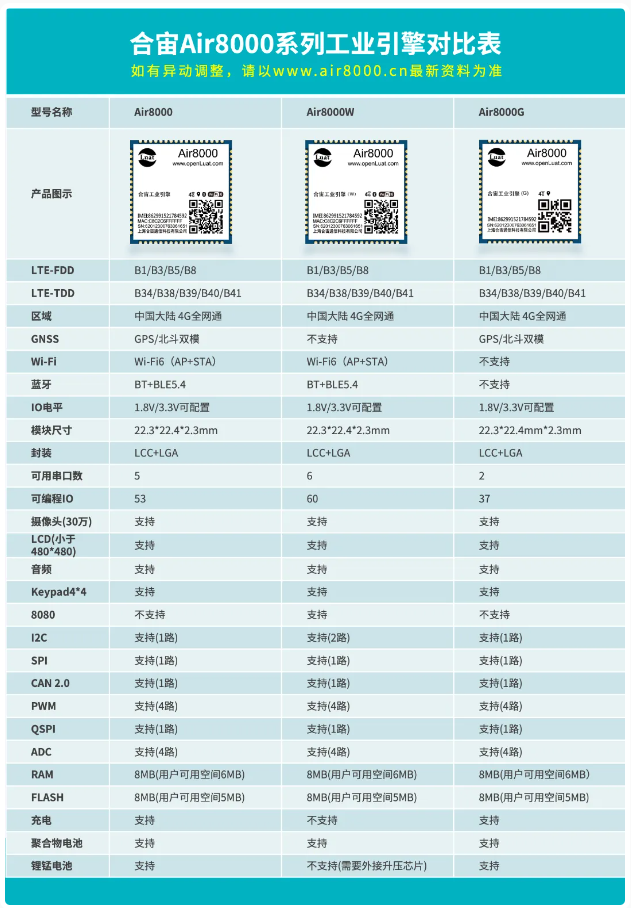
聊一聊:Air8000能解决哪些社会问题?
Air8000能解决什么社会问题呢?当前我们认为可以解决如下的问题:
问题一
硬件:成本高,备货压力大,稳定性差
嵌入式的一些常用的功能,比如GPIO、4G、Wi-Fi、蓝牙、定位、充电、升压、处理器等等,是项目上常用的功能。
如果每个都是模块,组合起来成本不菲。
Air8000的定价…
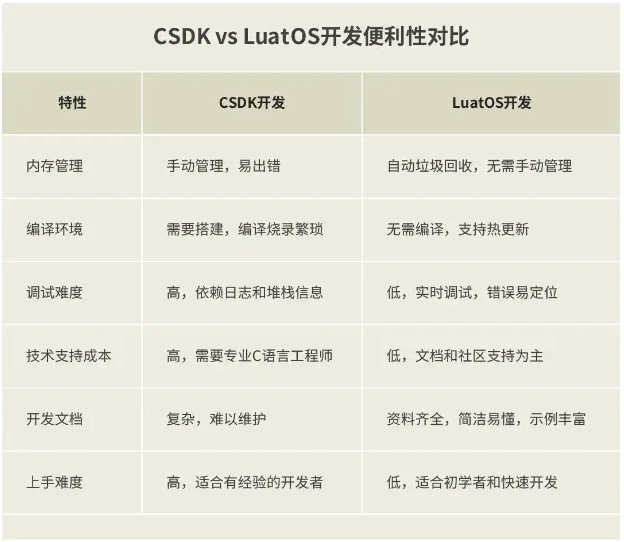
Open开发:CSDK与LuatOS的深度剖析
究竟要不要支持CSDK开发?
我们先来了解一下4G模组的软件架构。目前,4G模组内部的软件架构无一例外都是用C语言开发的,仅在底层使用了少量汇编语言。
从技术角度看,让用户使用C语言开发应用似乎顺理成章。毕竟C语言功能强大,运行效率极高。
然而,C语言在物联网行业的应用存…
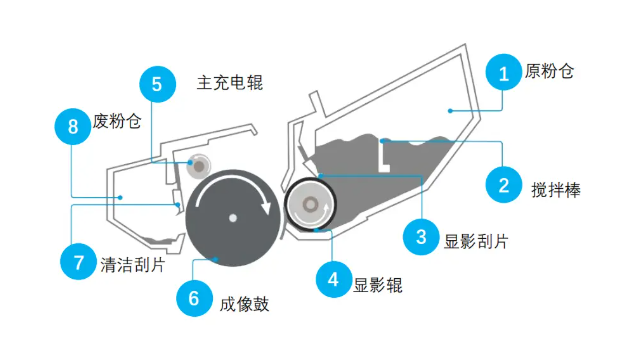
硒鼓内部结构示意图和功能说明
公司有一台惠普打印机,型号:HP Color LaserJet MFP M281fdw,更换硒鼓的成本是打印机最大的支出,最近在研究自己给墨盒加粉,直接买碳粉+芯片成本还是比较乐观的。
这里说明下,为什么要买芯片,买回来的一个全新的硒鼓是带有芯片的,然后装上打印机,可以看到该墨盒的使用情…
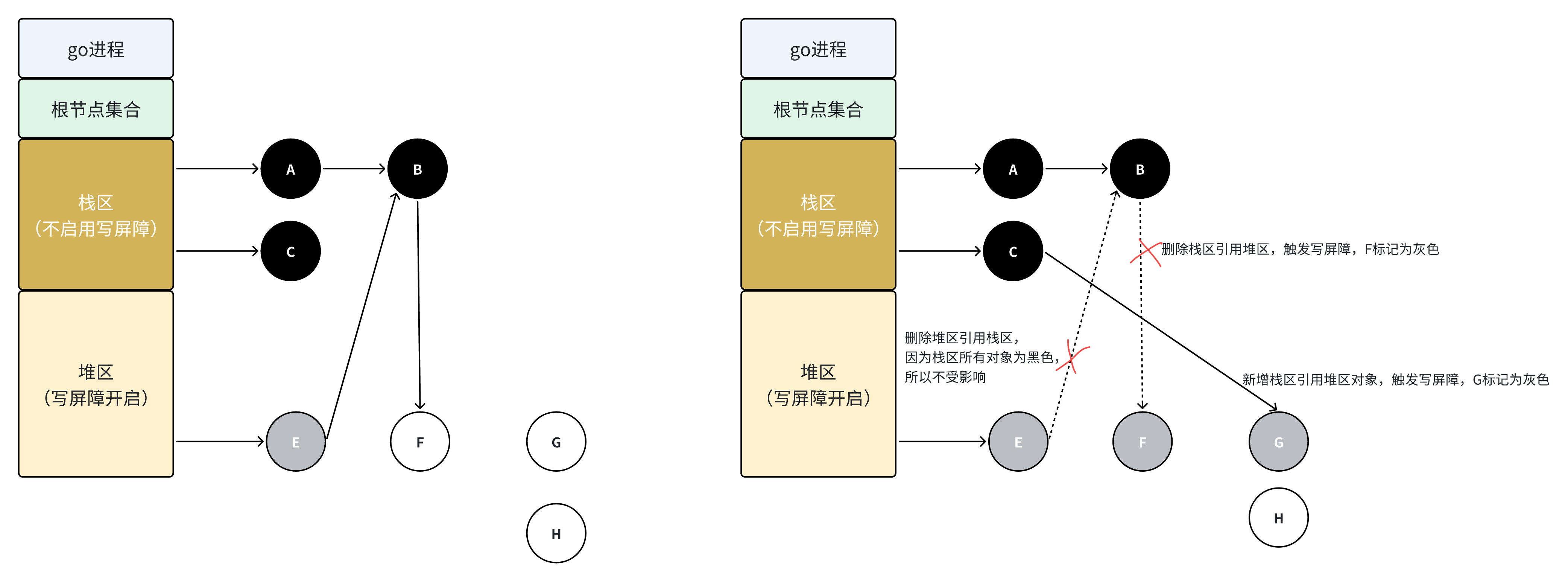
浅析Golang的内存管理(下篇):go垃圾回收机制
文章目录三色标记算法
混合写屏障
并发、增量回收机制
GC触发时机go语言作为内存托管类型的开发语言,go runtime提供了自动的内存管理机制,无需程序员手动管理对象的内存释放,go runtime会在合适的时机自动释放不需要的内存对象。
一、三色标记算法传统的内存对象标记算法早…
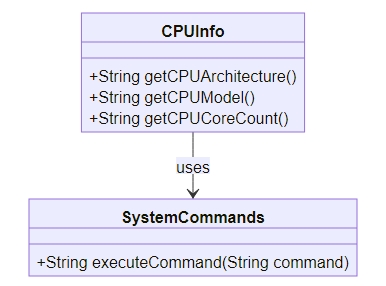
linux怎么判断服务器的cpu架构
在部署应用程序和服务时,确认服务器的CPU架构是非常重要的,因为这会直接影响软件的兼容性和性能。在Linux系统中,有许多方法可以获取服务器的CPU架构信息。本篇文章将介绍几种常用的方法,并提供代码示例,帮助用户有效地获取这个信息。
1. CPU架构的概念
CPU架构是指中央处…
低代码在项目管理中的5大实战案例:不懂代码也能快速搭建系统!
作为项目管理领域的“老司机”,我见过太多团队因传统开发效率低、需求响应慢而错失机会。低代码平台的崛起,让业务人员也能快速搭建系统,大幅缩短交付周期。以下是5个典型场景的实践案例,用最通俗的语言讲透核心逻辑👇案例1:3天上线CRM系统(客户关系管理)
背景:某销售…
[字符串算法]Manacher
我将永远追随六花的脚步1.前置知识
回文子串 回文的子串
最长回文子串 字符串中最长的回文子串
回文半径 设以\(i\)为中心的最大回文子串的长度为\(n\),则这个字符串第\(i\)位的回文半径为\((n+1)/2\)
2.算法流程
2.1 预处理
在处理回文子串(马拉车算法适用)的问题时…
StrokesPlus【电脑鼠标键盘手势软件】v0.5.8.0 中文绿色便携版
点击上方蓝字关注我
前言
StrokesPlus.net是一个超方便的手势识别软件,它能帮你用手势来代替鼠标和键盘操作。用起来既简单又灵活,功能还特别强大。
操作起来非常简单,它有好多实用的功能,比如智能识别你写的字、设定手势操作的区域、模拟鼠标的各种动作、运行脚本、响应窗…
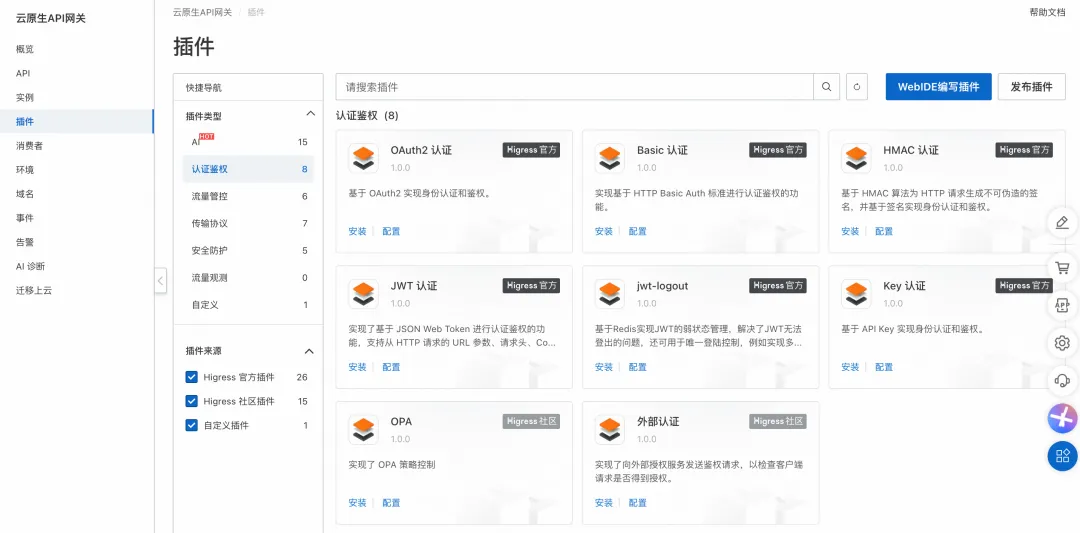
大模型推理主战场:什么才是通信协议标配?
关键词:# DeepSeek ;# SSE ;# WebSocketSSE 和 WebSocket 是什么?
大模型应用出现前的主流网络通信协议是什么?
为什么大模型应用没有沿用 Web 类应用的主流通信协议?
为什么 SSE 和 WebSocket 更适合支持大模型应用?
实时通信协议的技术挑战和应对方案
Whats Next?Dee…


![[字符串算法]Manacher](https://cdn.luogu.com.cn/upload/image_hosting/9mjwbp8c.png)
![[数据结构]树](https://cdn.luogu.com.cn/upload/image_hosting/oe363ck8.png)