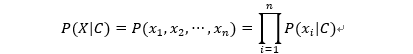写了这么久终于过了,发篇题解记录一下。
第一次写黑题题解,写的不好请见谅。
目录
- 本题思路
- 三点定圆
- 最小圆覆盖
- 关于最小圆覆盖时间复杂度
- 回到本题
- 二分法划分点集
- 总时间复杂度
- 最小覆盖双圆问题代码
本题思路
首先,这道题叫做最小覆盖双圆问题,这道题涉及到一个叫做最小圆覆盖的问题。
一个容易想到的思路:若我们能做出最小圆覆盖的问题,就可以把本题分成两个圆,也就是两个点集来处理。
那我们如何处理最小圆覆盖的问题呢?
三点定圆
首先,不共线的三个点可以确定一个圆。
作任意两点所在线段的中垂线,三条中垂线的交点就是这三个点共圆的圆心。这个圆心到三点中的任意一点就是这个圆的半径。当三点不在同一条直线时。形成一个三角形,而三角形有且只有一个外接圆。
数学原理是中垂线上的点到线段两端的距离相等。两条中垂线的交点,到两条线段的距离都相等。所以,不在同一条直线的三点可以确定一个圆。
附三角形的外切圆半径公式:\(\frac{abc}{4S}\),其中,\(S\) 表示三角形的面积,\(a\) 和 \(b\) 和 \(c\) 分别为三角形的三条边。
本部分代码:
Point circle_center(const Point a,const Point b,const Point c){Point center;double a1=b.x-a.x,b1=b.y-a.y,c1=(a1*a1+b1*b1)/2;double a2=c.x-a.x,b2=c.y-a.y,c2=(a2*a2+b2*b2)/2;double d=a1*b2-a2*b1;center.x=a.x+(c1*b2-c2*b1)/d;center.y=a.y+(a1*c2-a2*c1)/d;return center;
}
最小圆覆盖
根据以上结论,我们知道对于任意三个不共线的点,我们可以求出三点定圆,所以一个明显的想法就是枚举三个点。
具体步骤如下:
-
枚举第一个点 \(i\),若不在目前圆内,设它为圆心。
-
枚举第二个点 \(j\),若不在当前圆内,设当前圆为以 \(i\) 和 \(j\) 为直径的圆。
-
枚举第三个点 \(k\),若不在当前圆内,设当前圆为 \(i\) 和 \(j\) 和 \(k\) 的外接圆。
显然最优解一定是两个点为直径的圆或者一个三角形的外接圆,否则肯定能缩的更小。这样做就是正确的。
这就是所谓的增量法。
关于最小圆覆盖时间复杂度
显然,按上面的做法,时间复杂度是 \(O(n^3)\) 的,会被不良心的出题人卡掉。
所以,我们需要打乱数据,从而提升时间复杂度。
这就是所谓的随机增量法。
时间复杂度期望 \(O(n)\)。
最小圆覆盖代码:
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define eps 1e-8
const int N=1e5+1;
int sgn(double x){if(fabs(x)<eps) return 0;else return x<0?-1:1;
}
struct Point{double x,y;};
double Distance(Point A,Point B){return hypot(A.x-B.x,A.y-B.y);};
Point circle_center(const Point a,const Point b,const Point c){Point center;double a1=b.x-a.x,b1=b.y-a.y,c1=(a1*a1+b1*b1)/2;double a2=c.x-a.x,b2=c.y-a.y,c2=(a2*a2+b2*b2)/2;double d=a1*b2-a2*b1;center.x=a.x+(c1*b2-c2*b1)/d;center.y=a.y+(a1*c2-a2*c1)/d;return center;
}
void min_cover_circle(Point *p,int n,Point &c,double &r){random_shuffle(p,p+n);c=p[0],r=0;for(int i=1;i<n;i++){if(sgn(Distance(p[i],c)-r)>0){c=p[i];r=0;for(int j=0;j<i;j++){if(sgn(Distance(p[j],c)-r)>0){c.x=(p[i].x+p[j].x)/2;c.y=(p[i].y+p[j].y)/2;r=Distance(p[j],c);for(int k=0;k<j;k++){if(sgn(Distance(p[k],c)-r)>0){c=circle_center(p[i],p[j],p[k]);r=Distance(p[i],c);}}}}}}
}
Point p[N];
signed main(){int n;cin>>n;for(int i=0;i<n;i++) cin>>p[i].x>>p[i].y;Point c;double r;min_cover_circle(p,n,c,r);printf("%.10f\n%.10f %.10f\n",r,c.x,c.y);return 0;
}
最小圆覆盖例题:这里。
回到本题
之前说若我们能做出最小圆覆盖的问题,就可以把本题分成两个圆,也就是两个点集来处理。
现在我们已经会了最小圆覆盖的问题,如何划分点集呢?
如果暴力枚举,显然不行。
这时引出我们的二分法。
二分法划分点集
用二分求出一条与 \(X\) 轴垂直的直线,然后再求解。
如果正解是斜着画一条直线呢?
这时,我们旋转坐标系!
每次旋转之后都求一次最小双圆覆盖,然后再取最优值即是答案。如何对每个点进行“旋转”?
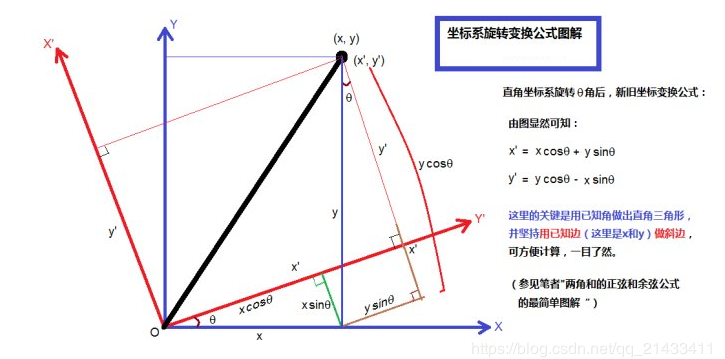
可以看图来理解。
坐标系旋转 \(180\) 度就是原坐标系了,所以只要转 \(180\) 度就好了。
总时间复杂度
首先,要转 \(180\) 次,每次中要二分直线,再做最小圆覆盖。
总时间复杂度 \(O(n \log n)\)。
最小覆盖双圆问题代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define eps 1e-8
int n;
const int N=1e5+1;
struct Point{double x,y;};
Point p[N],a[N];
double Distance(Point A,Point B){return hypot(A.x-B.x,A.y-B.y);};
int cmp(Point a, Point b){return a.x<b.x;}
int sgn(double x){if(fabs(x)<eps) return 0;else return x<0?-1:1;
}
Point rotate(const Point &b) {Point t;t.x=b.x*cos(1.0/180*acos(-1))+b.y*sin(1.0/180*acos(-1));t.y=b.y*cos(1.0/180*acos(-1))-b.x*sin(1.0/180*acos(-1));return t;
}
Point circle_center(const Point a,const Point b,const Point c){Point center;double a1=b.x-a.x,b1=b.y-a.y,c1=(a1*a1+b1*b1)/2;double a2=c.x-a.x,b2=c.y-a.y,c2=(a2*a2+b2*b2)/2;double d=a1*b2-a2*b1;center.x=a.x+(c1*b2-c2*b1)/d;center.y=a.y+(a1*c2-a2*c1)/d;return center;
}
double min_cover_circle(int n1,int n2){if(n1>n2) return 0;for(int i=n1;i<=n2;i++) a[i]=p[i];random_shuffle(a+n1+1,a+n2+1);Point c=a[n1];double r=0;for(int i=n1;i<=n2;i++){if(sgn(Distance(a[i],c)-r)>0){c=a[i];r=0;for(int j=n1;j<i;j++){if(sgn(Distance(a[j],c)-r)>0){c.x=(a[i].x+a[j].x)/2;c.y=(a[i].y+a[j].y)/2;r=Distance(a[j],c);for(int k=n1;k<=j;k++){if(sgn(Distance(a[k],c)-r)>0){c=circle_center(a[i],a[j],a[k]);r=Distance(a[i],c);}}}}}}return r;
}
void init(int n){double R=1e9;for(int i=1;i<=n;i++) cin>>p[i].x>>p[i].y;for(int i=1;i<=180;i++){ for(int i=1;i<=n;i++) p[i]=rotate(p[i]);sort(p+1,p+n+1,cmp);int l=1,r=n;while(l<=r) {int mid=(l+r)/2;double R1=min_cover_circle(1,mid),R2=min_cover_circle(mid+1,n);if(min(R1,R2)>R) break; if(R1<R2)l=mid+1;else r=mid-1;R=min(R,max(R1, R2));}}printf("%.2f\n",R);
}
signed main(){while(cin>>n&&n!=0){init(n);}return 0;
}
如果本篇题解还可以,就点个赞吧!