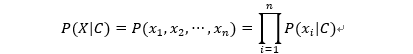2.27 CW 模拟赛 T1. 麻将

前言

• 定义合法情况, 要求输出一组合法情况 / 合法情况的最值问题 / 求方案数
  • 往往利用 \(\rm{dp}\) , 结合约束处理当前方案数
    • 关注构造方案 / 顺序
    • 关注本质重复的转移是否存在
  • 先找到一组合法解, 然后在基础上进行调整
  • 找到所有情况统一的构造方案

思路

题意

给定 $n$ 个位置, 第 $i$ 个位置是牌 $a_i$
求有多少种把牌划分成面子的方法

即形如 $\{x, x, x\} \textrm{ or } \{x, x + 1, x + 2\}$ 的连续段

首先因为原串上不好处理, 而且明确给了值域, 所以不难想到转移到值域上去思考

考虑一个合法解的构造过程
在值域上从前往后扫, 每次挑选符合题意的一个连续段然后对值域数组进行更新

一些小问题

首先, 不能简单地对值 $i$ 分类讨论成

• $(1)$ 作为 $a$ 个 $\{i, i, i\}$
• $(2)$ 作为 $b$ 个 $\{i, i + 1, i + 2\}$
  以此清空 $i, i + 1, i + 2$ 对应的数量

原因是对于一些情况
按照上面的方法, 不会考虑到先对 $i, i + 1, i + 2$ 做操作, 然后再对 $i + 1, i + 2, i + 3$ 做操作使 $i + 1, i + 2$ 清空

也就是说, 这样转移被严格限制了, 不可能生成其他情况的 $(2)$ 操作
因此是不行的

---

赛时为了解决上面的问题, 换成了对值域的区间 $\rm{dp}$
但是这个问题更加明显
假设对于区间 $\{a, b, c\}$ , 容易发现如果用区间 $\rm{dp}$ , 会分成

• 清空 $\{b, c\}$ , 在清空 $a$
• 清空 $\{a, b\}$ , 在清空 $c$

不难发现在本质上极容易重复, 并且不易去重

综上, 如何找到一个好的方法来 \(\rm{dp}\) 呢
要满足两个需求

• 顺序必须严格钦定
• 必须考虑到所有可能的操作区间

因此不难想到对最初的 \(\rm{dp}\) 做一些修改
并不钦定一定要在当前对 \(i\) 的操作清空 \(i, i + 1, i + 2\) , 而是只钦定清空 \(i - 2\) , 因为再不清空就没机会了

不难想到状态定义
令 \(f_{i, j, k}\) 表示值域上考虑到 \(i\) , \(i - 1\) 还剩下 \(j\) 个, \(i - 2\) 还剩下 \(k\) 个的方案数

因为每次转移只考虑 \(i, i - 1, i - 2\)
不难发现我们可以钦定每次操作只对 \(i\) 进行 \(3\) 连操作, 然后对 \(\{i, i - 1, i - 2\}\) 进行操作
这样可以避免重复

所以枚举对 \(i\) 进行 \(q\) 次 \(3\) 连操作 , 现在 \(i\) 出现 \(w_i - 3q\) 次
然后剩下必须进行 \(i - 2\) 次操作, 转移即可

实现

框架

如上转移即可

代码

#include <bits/stdc++.h>
const int MOD = 1e9 + 7;
const int MAXN = 5206; // 41
namespace calc {int add(int a, int b) { return a + b >= MOD ? a + b - MOD : a + b; }int mus(int a, int b) { return a - b < 0 ? a - b + MOD : a - b; }int mul(int a, int b) { return (a * b * 1ll) % MOD; }void addon(int &a, int b) { a = add(a, b); }void mulon(int &a, int b) { a = mul(a, b); }
} using namespace calc;int n, m;
int p[MAXN];
int dp[2][MAXN][MAXN];int now = 0, nxt = 1;/*初始化*/
void init() {if (m == 1 || m == 2) {int ans = 1; for (int i = 1; i <= m; i++) if (p[i] % 3) ans = 0;printf("%d", ans);exit(0);}for (int i = 0; i <= p[1]; i += 3) for (int j = 0; j <= p[2]; j += 3) dp[now][p[2] - j][p[1] - i] = 1;
}signed main()
{scanf("%d %d", &n, &m);for (int i = 1, tmp; i <= n; i++) scanf("%d", &tmp), p[tmp]++;init();for (int i = 3; i <= m; i++) {/*初始化*/ for (int j = 0; j <= p[i]; j++) for (int k = 0; k <= p[i - 1]; k++) dp[nxt][j][k] = 0;for (int j = 0; j <= p[i - 1]; j++) for (int k = 0; k <= std::min(p[i - 2], j); k++) {for (int q = 0; q <= p[i] && p[i] - q >= k; q += 3) {addon(dp[nxt][p[i] - q - k][j - k], dp[now][j][k]);}}std::swap(now, nxt);}printf("%d", dp[now][0][0]);return 0;
} 

总结

一类只钦定消除 不消除以后就不能消除的元素 的 \(\rm{dp}\)
一般记录到达 不消除以后就不能消除的元素 之前的元素还剩下多少个来处理

往往一种操作只用一次转移考虑才能做到去重

---

关于这道题的一些额外理解

首先, 一组合法情况可以视作对值域数组 $w$ 的一个构造

• 对于 $w_i$ , 进行 $p$ 次操作构造 $p$ 个 $\{i, i, i\}$
• 对于任意 $w_i, w_{i - 1}, w_{i - 2}$ , 进行 $q$ 次操作

如果恰好把 $w$ 归零, 即是合法构造

因此我们枚举 $i$ 作为分界, 同时对这两个进行构造

类似于之前多重集排列那一部分, 这个问题同样可以表述为
求有多少组组 $x, y$ , 使其满足
$$\forall i, w_i - 3x_i - (y_i + y_{i + 1} + y_{i + 2}) = 0$$
然后稍微转化一下, 把 $y_i$ 的贡献拆成 $i, i - 1, i - 2$ 处的贡献, 就可以做 $\rm{dp}$ 了

这也是一种理解 $\rm{dp}$ 的方法, 即先把构造表示出来, 再面向构造做
一般适用于这种不常规的 $\rm{dp}$ 问题