最长公共子序列LCS 笔记
假设存在两个相同长度平凡的序列,我们希望找到它们最长的公共子序列,在没有其他特殊条件的情况下,利用动态规划计算的时间复杂度为 \(O(n^2)\) ,并且可以记录这个子序列
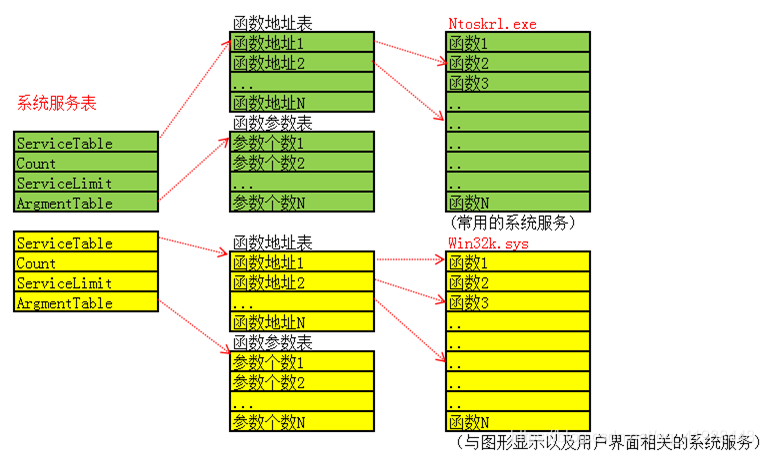
考虑两个指针作用于两个序列上,记 \(dp_{i,j}\) 表示为连续子序列 \([a_1,a_i]\) 与 \([b_1,b_j]\) 上的最长公共子序列的长度
两个指针当前指向的元素存在两种可能性:
-
\(a_i=b_j\) ,说明 \(a_i,b_j\) 都能存在于要找的公共子序列中,状态转移为
\[dp_{i,j}=dp_{i-1,j-1}+1 \] -
\(a_i\ne b_j\) ,有两种可能
- \(a_i\) 不在公共子序列中,\(dp_{i,j}=dp_{i-1,j}\)
- \(b_j\) 不在公共子序列中,\(dp_{i,j}=dp_{i,j-1}\)
两种可能合并后,当前的 \(dp_{i,j}\) 取最优解,状态转移为
\[dp_{i,j}=max(dp_{i-1,j},dp_{i,j-1}) \]
最后考虑边界情况,即当 \(i=0,j=0\) 时,\(dp_{i,j}=0\) ,这意味着一个序列没有元素时无法找出公共子序列
dp[0][0]=0;
for (int i=1;i<=m;i++){for (int j=1;j<=n;j++){if (a[i]==b[j]) f[i][j]=f[i-1][j-1]+1;else f[i][j]=max(f[i][j-1],f[i-1][j]);}
}
如果需要记录所选的最长公共子序列,则要添加一个前驱数组 \(p\),表明状态的转移方向
for (int i=1;i<=m;i++){for (int j=1;j<=n;j++){if (a[i-1]==b[j-1]){dp[i][j]=dp[i-1][j-1]+1;p[i][j]=1;}else if (f[i][j-1]>f[i-1][j]){f[i][j]=f[i][j-1];p[i][j]=2;}else{f[i][j]=f[i-1][j];p[i][j]=3;}}
}
将两个序列拆分后,分别为表格的长宽
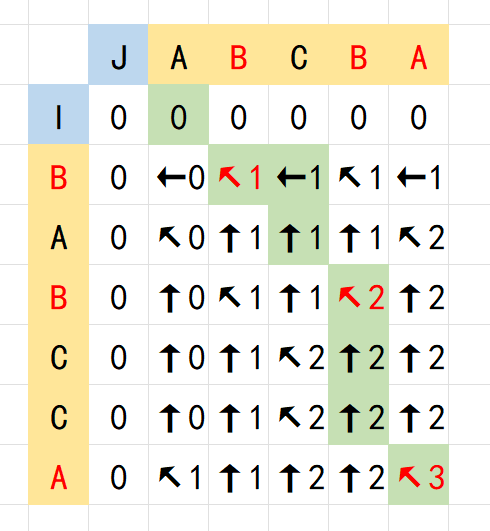
\(p=1,2,3\) 分别表示状态转移的方向,左上方,左边,上边
最后通过依次倒序访问 \(p\) 数组,根据 \(p_{i,j}\) 移动游标,得到公共子序列
int i=m,j=n,k=dp[m][n];
vector<char> s(k+10);
while (i>0&&j>0){if (p[i][j]==1){s[k--]=a[i-1];//记录公共子序列i--;j--;}else if (p[i][j]==2)j--;//移动游标elsei--;
}
for (int i=1;i<=k;i++)cout<<s[i];