逆序对的解法——归并排序

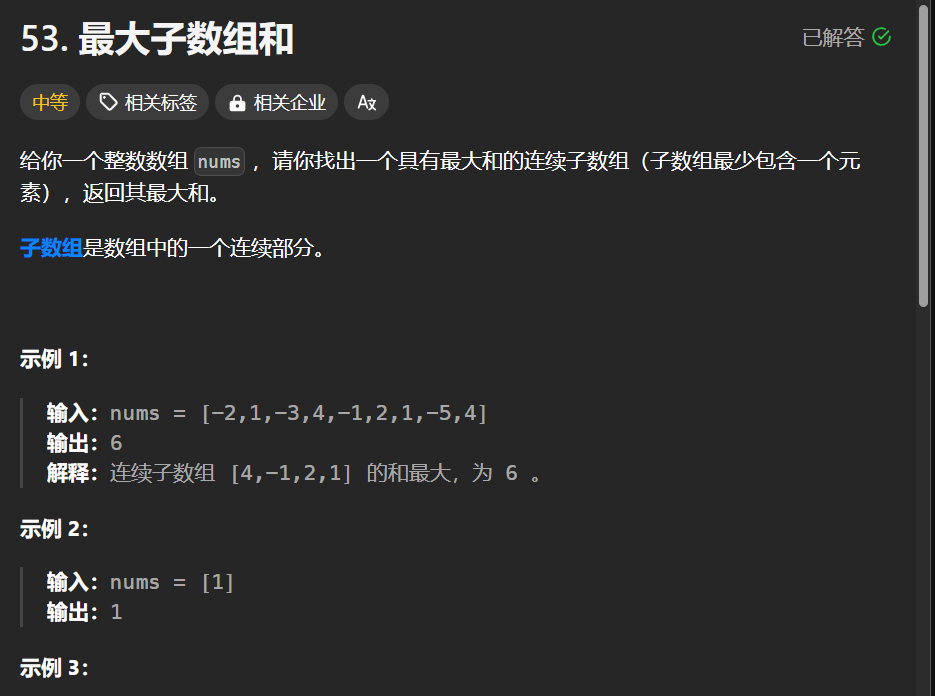
题目来源：洛谷P8613小朋友排队(https://www.luogu.com.cn/problem/P8613)
题目大意为：给你一段序列，只允许相邻两个数交换，对于某个数，一次操作ans+1，第二次操作ans+2，以此类推。问让此序列排列成递增序列的ans最小值。

思路： 当一个数左边存在比它大的数时，一定需要交换；同理，当它右边存在比它小的数字时，一定要交换。即求出整个序列中的逆序对个数。
求逆序对的方法之一为————归并排序

归并排序的原理
将一个序列不断二分，再在子序列中排序，再不断整合两个子序列，整合过程中利用双指针重新排序

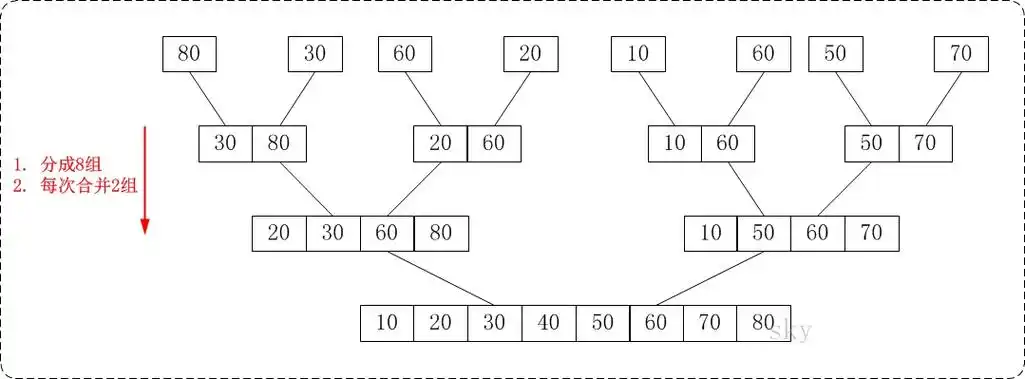
而在此基础上查找逆序对，就是在两个子序列合并时，利用双指针记录每个数的逆序对的个数。
难点一：在双指针遍历的同时需要重新在子序列中排序，需要定义一个新数组来存储新的子序列，遍历结束需要重新赋给原来数组
for(int i=first;i<=end;i++){ nums[i]=cpy[i]; }

难点二：在排序过程中，数字的位置会出现变化，逆序对个数不能记录在单独的数组中，必须和原来的数“绑定”，显然需要利用结构体struct

struct num{int order;int x;int count;
}nums[N],cpy[N];

在这里nums是原数组，cpy是每次合并排序时需要的备用数组，x为值，count记录此数字的逆序对个数。实现值和count的对应。

难点三：如何求出逆序对个数

while( p<=mid && q<=end ){if( nums[p].x <= nums[q].x ){nums[p].count+=q-mid-1;cpy[cnt]=nums[p];cnt++,p++;}else if( nums[p].x > nums[q].x ){nums[q].count+=mid-p+1;cpy[cnt++]=nums[q];q++;}}

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
struct num{int order;int x;int count;
}nums[N],cpy[N];
void merge(int first,int end){if( first == end ) return;int mid=(first+end)/2;merge( first, mid );merge( mid+1, end );int cnt=first,p=first,q=mid+1;while( p<=mid && q<=end ){if( nums[p].x <= nums[q].x ){nums[p].count+=q-mid-1;cpy[cnt]=nums[p];cnt++,p++;}else if( nums[p].x > nums[q].x ){nums[q].count+=mid-p+1;cpy[cnt++]=nums[q];q++;}}if( p<=mid ){for(;p<=mid;p++){nums[p].count+=end-mid;cpy[cnt++]=nums[p];}}if( q<=end ){for(;q<=end;q++){cpy[cnt++]=nums[q];}}for(int i=first;i<=end;i++){nums[i]=cpy[i];}return;
}
int main(){int n,x;long long ans=0;cin>>n;for(int i=0;i<n;i++)  { cin>>x; nums[i]={i,x,0}; }merge(0,n-1);for(int i=0;i<n;i++){long long d=nums[i].count;ans+=(1+d)*d/2;}cout<<ans<<endl;return 0;
}