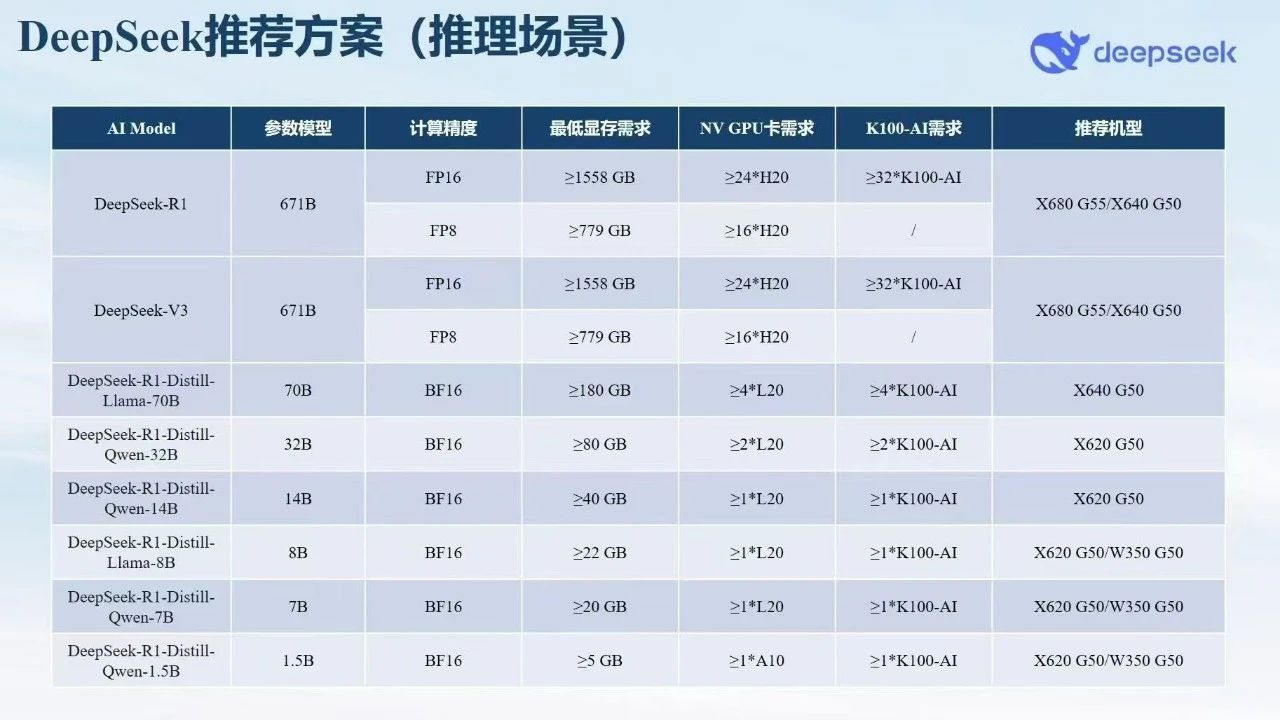
先来讲一下弱大数定律吧，这个比较好理解
弱大数定律的标准形式是这样的：
\[\forall \epsilon>0,\underset{n\rightarrow\infty}{\lim}P(|\bar{X}_n-\mu|<\epsilon)=1
\]
这里注意的是我们的极限符号是包含概率的，我们按照数列极限的定义将其写开：
\[\forall \epsilon>0,\forall\phi>0,\exists N,\forall n>N,1-P(|\bar{X}_n-\mu|<\epsilon)<\phi
\]
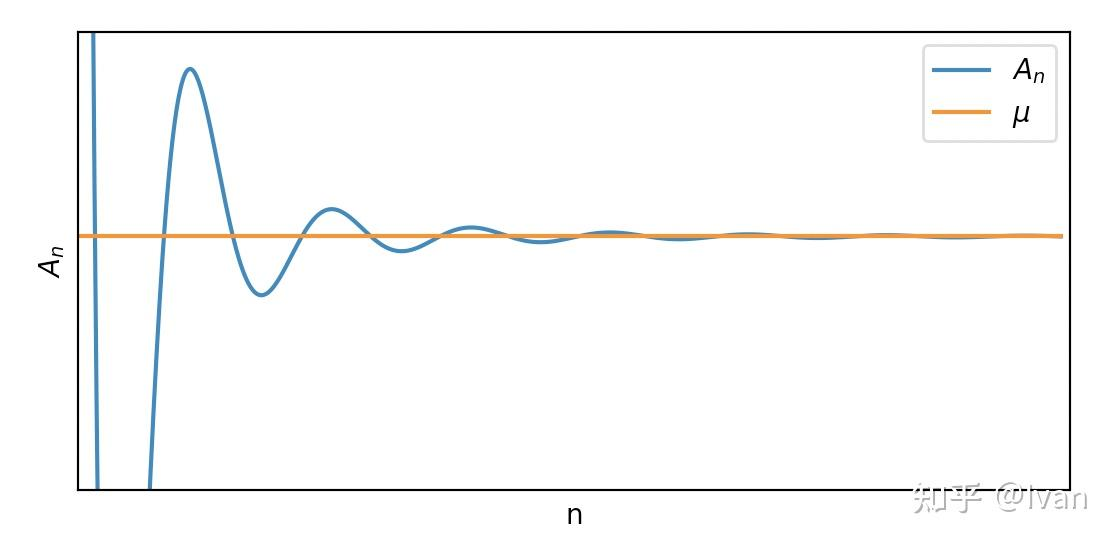
假设我们知道了\(X\)的分布，于是在确定了\(n\)的情况下就可以准确算出\(\bar{X}_n-\mu\)的分布，也就是说其实\(P(|\bar{X}_n-\mu|<\epsilon)\)是一个定了的数列（而不是随机变量）。不妨设\(P(|\bar{X}_n-\mu|<\epsilon)=1-\frac{1}{n}\)，显然满足弱大数定律，但是当我们固定了一个\(n\)之后，做多次实验（我们称一次实验包含\(n\)个独立的随机变量\(X\)）的话，是有可能样本均值偏离\(\mu\)的。画出来的图像见下
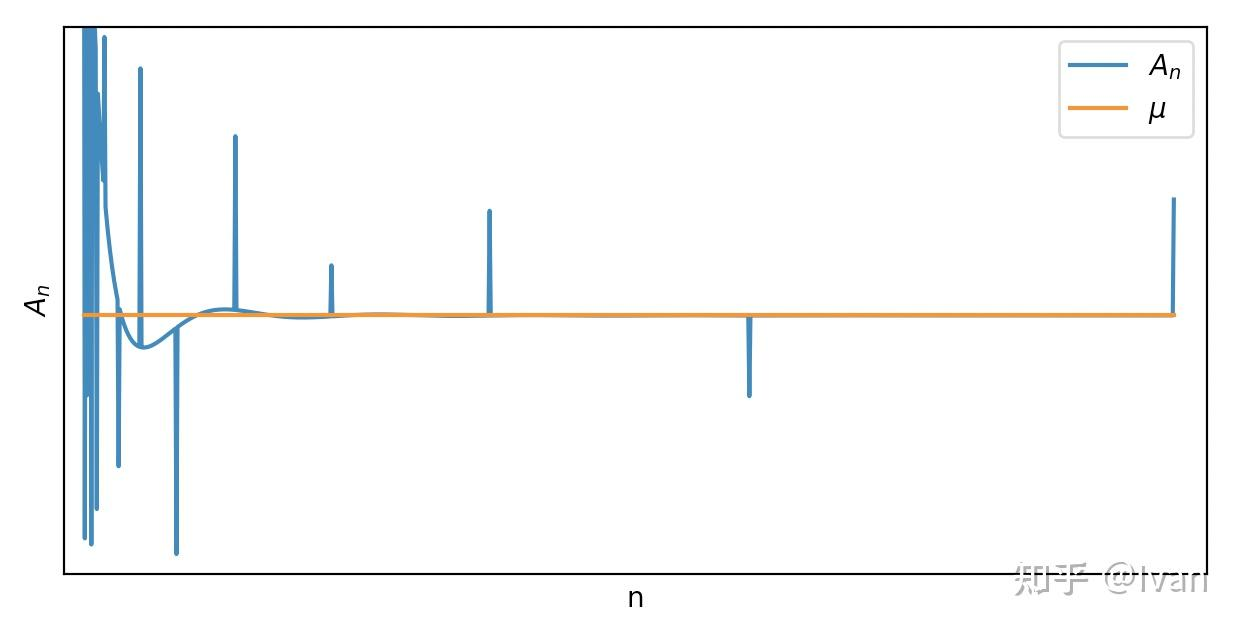
那么强大数定律的数学形式是这样的：
\[P(\underset{n\rightarrow\infty}{\lim}\bar{X}_n-\mu=0)=1
\]
我们用极限的定义写开，\(\underset{n\rightarrow\infty}{\lim}\bar{X}_n-\mu=0\iff\forall\epsilon>0,\exists N,\forall n>N,|\bar{X}_n-\mu|<\epsilon\)
那么注意，后者其实是一个事件，也就是我们给定了一个偏离量\(\epsilon\)，就可以找到了\(N\)，使得我们做的试验次数大于\(N\)的话，样本均值与均值的距离不会超过偏移量。那么这个事件是有一个发生概率的，而强大数定律就告诉我们，这个事件是必然事件。所以强大数定律画出来的图见下
