1、自由度是什么？怎么确定？

统计学上，自由度是指当以样本的统计量估计总体的参数时，样本中独立或能自由变化的数据个数叫自由度。一般来说，自由度等于独立变量减掉其衍生量数。举例来说，变异数的定义是样本减平均值(一个由样本决定的衍生量)，因此对N个随机样本而言，其自由度为N-1。

通俗点说，一个班上有50个人，我们知道他们语文成绩平均分为80，现在只需要知道49个人的成绩就能推断出剩下那个人的成绩。你可以随便报出49个人的成绩，但是最后一个人的你不能瞎说，因为平均分已经固定下来，自由度少一个。

2、正态分布检验自由度问题

在正态分布检验中，这里的M（三个统计量）为：N（总数）、平均数和标准差。

因为我们在做正态检验时，要使用到平均数和标准差以确定该正态分布形态，此外，要计算出各个区间的理论次数，我们还需要使用到N。

所以在正态分布检验中，自由度为K－3。

3、T检验

t检验适用于两个变量均数间的差异检验，多于两个变量间的均数比较要用方差分析。

无论哪种类型的t检验，都必须在满足特定的前提条件下: 正态性和方差齐性，应用才是合理的。这是因为必须在这样的前提下所计算出的t统计量才服从t分布，而t检验正是以t分布作为其理论依据的检验方法。

t检验是目前医学研究中使用频率最高，医学论文中最常见到的处理定量资料的假设检验方法。

4、统计学P值意义

结果的统计学意义是结果真实程度（能够代表总体）的一种估计方法。专业上，P值为结果可信程度的一个递减指标，P值越大，我们越不能认为样本中变量的关联是总体中各变量关联的可靠指标。

P值是将观察结果认为有效即具有总体代表性的犯错概率。如P=0.05提示样本中变量关联有5%的可能是由于偶然性造成的。即假设总体中任意变量间均无关联

我们重复类似实验，会发现约20个实验中有一个实验，我们所研究的变量关联将等于或强于我们的实验结果。（这并不是说如果变量间存在关联，我们可得到5%或95%次数的相同结果，当总体中的变量存在关联，重复研究和发现关联的可能性与设计的统计学效力有关。）

在许多研究领域，0.05的P值通常被认为是可接受错误的边界水平。

5、如何判定结果具有真实的显著性

在最后结论中判断什么样的显著性水平具有统计学意义，不可避免地带有武断性。换句话说，认为结果无效而被拒绝接受的水平的选择具有武断性。

实践中，最后的决定通常依赖于数据集比较和分析过程中结果是先验性还是仅仅为均数之间的两两比较，依赖于总体数据集里结论一致的支持性证据的数量，依赖于以往该研究领域的惯例。

通常，许多的科学领域中产生P值的结果≤0.05被认为是统计学意义的边界线，但是这显著性水平还包含了相当高的犯错可能性。结果 0.05≥P>0.01被认为是具有统计学意义，而0.01≥P≥0.001被认为具有高度统计学意义。但要注意这种分类仅仅是研究基础上非正规的判断常规。

6、所有的检验统计都是正态分布的吗？

并不完全如此，但大多数检验都直接或间接与之有关，可以从正态分布中推导出来，如t检验、F检验或卡方检验。这些检验一般都要求：所分析变量在总体中呈正态分布，即满足所谓的正态假设。许多观察变量的确是呈正态分布的，这也是正态分布是现实世界的基本特征的原因。

随着样本量的增加，样本分布形状趋于正态，即使所研究的变量分布并不呈正态。

7、假设检验的内涵及步骤

答：在假设检验中，由于随机性我们可能在决策上犯两类错误，一类是假设正确，但我们拒绝了假设，这类错误是“弃真”错误，被称为第一类错误；

一类是假设不正确，但我们没拒绝假设，这类错误是“取伪”错误，被称为第二类错误。

一般来说，在样本确定的情况下，任何决策无法同时避免两类错误的发生，即在避免第一类错误发生机率的同时，会增大第二类错误发生的机率；或者在避免第二类错误发生机率的同时，会增大第一类错误发生的机率。人们往往根据需要选择对那类错误进行控制，以减少发生这类错误的机率。大多数情况下，人们会控制第一类错误发生的概率。

发生第一类错误的概率被称作显著性水平，一般用α表示，在进行假设检验时，是通过事先给定显著性水平α的值而来控制第一类错误发生的概率。

在这个前提下，假设检验按下列步骤进行：

1）确定假设；

2）进行抽样，得到一定的数据；

3）根据假设条件下，构造检验统计量，并根据抽样得到的数据计算检验统计量在这次抽样中的具体值；

4）依据所构造的检验统计量的抽样分布，和给定的显著性水平，确定拒绝域及其临界值；

5）比较这次抽样中检验统计量的值与临界值的大小，如果检验统计量的值在拒绝域内，则拒绝假设；

到这一步，假设检验已经基本完成，但是由于检验是利用事先给定显著性水平的方法来控制犯错概率的，所以对于两个数据比较相近的假设检验，我们无法知道那一个假设更容易犯错，即我们通过这种方法只能知道根据这次抽样而犯第一类错误的最大概率（即给定的显著性水平），而无法知道具体在多大概率水平上犯错。

计算 P值有效的解决了这个问题，P值其实就是按照抽样分布计算的一个概率值，这个值是根据检验统计量计算出来的。通过直接比较P值与给定的显著性水平α的大小就可以知道是否拒绝假设，显然这就代替了比较检验统计量的值与临界值的大小的方法。

而且通过这种方法，我们还可以知道在p值小于α的情况下犯第一类错误的实际概率是多少，p＝0.03<α=0.05，那么拒绝假设，这一决策可能犯错的概率是0.03。需要指出的是，如果P>α，那么假设不被拒绝，在这种情况下，第一类错误并不会发生。

8、卡方检验的结果，值是越大越好，还是越小越好？

与其它检验一样，所计算出的统计量越大，在分布中越接近分布的尾端，所对应的概率值越小。如果试验设计合理、数据正确，显著或不显著都是客观反映。没有什么好与不好。

9、在比较两组数据的率是否相同时，二项分布和卡方检验有什么不同？

卡方分布主要用于多组多类的比较，是检验研究对象总数与某一类别组的观察频数和期望频数之间是否存在显著差异，要求每格中频数不小于5，如果小于5则合并相邻组。

二项分布则没有这个要求。如果分类中只有两类还是采用二项检验为好。如果是2*2表格可以用fisher精确检验，在小样本下效果更好

10、如何比较两组数据之间的差异性

从三个方面来回答，

1）设计类型是完全随机设计两组数据比较，不知道数据是否是连续性变量？

2）比较方法：如果数据是连续性数据，且两组数据分别服从正态分布和方差齐性检验，则可以采用t检验，如果不服从以上条件可以采用其他检验。

3）想知道两组数据是否有明显差异？不知道这个明显差异是什么意思？是问差别有无统计学意义（即差别的概率有多大）还是两总体均数差值在哪个范围波动？如果是前者则可以用第2步可以得到P值，如果是后者，则是用均数差值的置信区间来完成的。

11、什么是辛普森悖论?为什么会出现？

细分的结果和整体的结果相悖，这就是我们常说的辛普森悖论。辛普森悖论主要是因为2组样本不均衡，抽样不合理。正确的试验实施方案里，除被测试的变量外，其他可能影响结果的变量的比例都应该保持一致，这就需要对流量进行均匀合理的分割。例如：

如原来男性20人，点击1人；女性100人，点击99人，总点击率100/120。

现在男性100人，点击6人；女性20人，点击20人，总点击率26/120。

男生和女生的点击率虽然都增加了，但是由于点击率更高的女生所占的比例过小，未能拉动整体的点击率上升。

12、协方差与相关系数的区别和联系

协方差：

协方差表示的是两个变量的总体的误差，这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。

相关系数：

研究变量之间线性相关程度的量，取值范围是[-1,1]。相关系数也可以看成协方差：一种剔除了两个变量量纲影响、标准化后的特殊协方差。

13、AB测试统计显著但实际不显著是什么原因？

这个可能的原因是我们在AB测试当中所选取的样本量过大，导致和总体数据量差异很小，这样的话即使我们发现一个细微的差别，它在统计上来说是显著的，在实际的案例当中可能会变得不显著了。

举个栗子，对应到我们的互联网产品实践当中，我们做了一个改动，APP的启动时间的优化了0.001秒，这个数字可能在统计学上对应的P值很小，也就是说统计学上是显著的，但是在实际中用户0.01秒的差异是感知不出来的。那么这样一个显著的统计差别，其实对我们来说是没有太大的实际意义的。所以统计学上的显著并不意味着实际效果的显著。

14、怎么理解中心极限定理？

中心极限定理定义：

（1）任何一个样本的平均值将会约等于其所在总体的平均值。

（2）不管总体是什么分布，任意一个总体的样本平均值都会围绕在总体的平均值周围，并且呈正态分布。

中心极限定理作用：

（1）在没有办法得到总体全部数据的情况下，我们可以用样本来估计总体。

（2）根据总体的平均值和标准差，判断某个样本是否属于总体。

15、怎么给小孩子讲解正态分布？

拿出小朋友班级的成绩表，每隔2分统计一下人数（因为小学一年级大家成绩很接近），画出钟形。然后说这就是正态分布，大多数的人都集中在中间，只有少数特别好和不够好，拿出隔壁班的成绩表，让小朋友自己画画看，发现也是这样的现象，然后拿出班级的身高表，发现也是这个样子的。

大部分人之间是没有太大差别的，只有少数人特别好和不够好，这是生活里普遍看到的现象，这就是正态分布。

16、您在机器学习解决方案中的哪些地方使用了假设检验?

假设检验是一种统计分析,我们在其中检验针对任何特定情况所做的假设。在测试一些声称为真的假设时,我进行了假设测试,其中零假设是任何声称的结果都是真实的,而替代假设是任何声称都是错误的。

17、你对P值的理解是什么?它在机器学习中的用途是什么?

P值也称为概率值,它是零假设为真的概率。它设置了拒绝零假设的规则。

如果 p 值小于显着性值,则我们拒绝原假设或接受它。

如果 p 值落在 95% 的置信区间内,那么我们将接受原假设。

18、我们可以将卡方与数值数据集一起使用吗?如果是,请举例。如果不是,请给出理由。

卡方通常处理分类数据,而不仅仅是数值数据。

卡方求出差异或将两个或多个组与一个值进行比较,或比较两个或多个组。

19、您对 ANOVA 测试的理解是什么?

ANOVA 代表方差分析。它是 T 检验的扩展。

在 T-Test 中,我们测试平均值是否存在差异,并且一次只能测试两组,因此如果有超过 2 组而不是多次执行 T-Test,我们会进行 ANOVA 测试。

ANOVA 测试寻找两种不同类型的变化:

组内变异

组间变异为了检验 ANOVA,我们的假设将是:

零假设:均值没有差异

替代假设:至少或均值不同于其他均值

有两种类型的方差分析:

单向方差分析

双向方差分析

单向方差分析:当我们要测试两组并查看是否有任何差异时。

双向方差分析:当我们对同一组进行两次测试时。

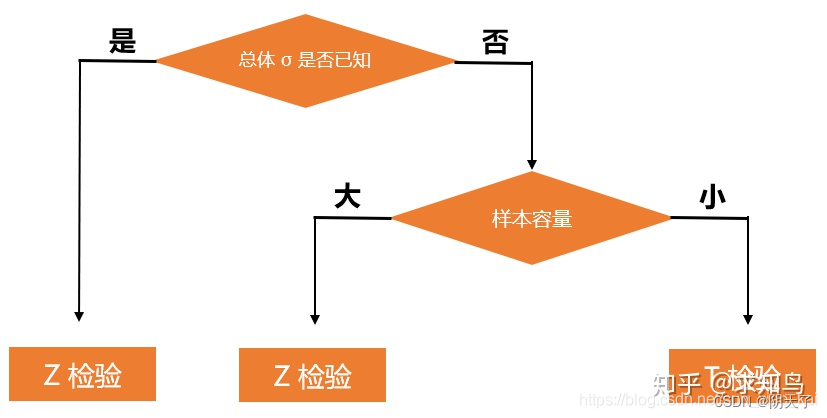
20、给我一个我们可以使用 Z 检验和 T 检验的场景

我们根据以下条件使用任一测试:

样本量:

当样本量大或大于 30 时,我们使用 Z 检验,否则使用 T 检验

人口差异:

当总体方差已知时,我们使用 Z 检验,否则使用 T 检验

分配:

如果是正态分布,我们执行 Z 测试,否则执行 T 测试

21、当您尝试计算标准差或方差时,为什么在分母中使用 n-1?

将分母设为 n-1 可以纠正总体方差估计中的偏差。

例如:

如果我们有总体平均值不在样本点内的数据点
现在为* ,如果我们取样本均值以及样本点与样本均值之间的距离,那么与总体方差相比,估计值将低得多

这可能导致低估总体方差

因此,通过将分母除以 n-1,这使得分母更小,进而为样本方差提供了高值,这就是无偏估计

22、您如何理解右偏度?举个例子

当数据不是正态分布时,我们在右侧有尾型的拉长线,称为右偏度。
例如：收入分配

23、正态分布、标准正态分布和均匀分布有什么区别?

正态分布

它是一个密度曲线,它是一个钟形曲线

具有数据聚集在中心值附近的趋势,中心值也称为总体均值

总面积100%

标准正态分布

它是一种特殊的正态分布,其均值为 0,标准差为 1
均匀分布

此分布的值位于某个范围/边界之间

24、参数估计的两种方法：最小二乘估计和最大似然估计

最小二乘法：为了选出使得模型输出与系统输出尽可能接近的参数估计值，可用模型与系统输出的误差的平方和来度量接近程度。使误差平方和最小的参数值即为所求的估计值。

极大似然法：选择参数，使已知数据在某种意义下最可能出现。某种意义是指似然函数最大，这里似然函数是数据Y的概率分布函数。与最小二乘法不同的是，极大似然法需要已知这个概率分布函数。

25、如何选择采用哪种假设检验？

Z检验：
一般用于大样本（即样本容量大于30）平均值差异性检验的方法。它是用标准正态分布的理论来推断差异发生的概率，从而比较两个平均数的差异是否显著。在国内也被称作u检验。

T检验：
主要用于样本含量较小（例如n < 30），总体标准差σ未知的正态分布。T检验是用t分布理论来推论差异发生的概率，从而比较两个平均数的差异是否显著。

卡方检验：
卡方检验是统计样本的实际观测值与理论推断值之间的偏离程度，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，如果卡方值越大，二者偏差程度越大；反之，二者偏差越小；若两个值完全相等时，卡方值就为0，表明理论值完全符合。