题目
2711. 对角线上不同值的数量差
给你一个下标从 0 开始、大小为 m x n 的二维矩阵 grid ,请你求解大小同样为 m x n 的答案矩阵 answer 。
矩阵 answer 中每个单元格 (r, c) 的值可以按下述方式进行计算:
- 令
topLeft[r][c]为矩阵grid中单元格(r, c)左上角对角线上 不同值 的数量。 - 令
bottomRight[r][c]为矩阵grid中单元格(r, c)右下角对角线上 不同值 的数量。
然后 answer[r][c] = |topLeft[r][c] - bottomRight[r][c]| 。
返回矩阵 answer 。
矩阵对角线 是从最顶行或最左列的某个单元格开始,向右下方向走到矩阵末尾的对角线。
如果单元格 (r1, c1) 和单元格 (r, c) 属于同一条对角线且 r1 < r ,则单元格 (r1, c1) 属于单元格 (r, c) 的左上对角线。类似地,可以定义右下对角线。
示例 1:

输入:grid = [[1,2,3],[3,1,5],[3,2,1]]
输出:[[1,1,0],[1,0,1],[0,1,1]]
解释:第 1 个图表示最初的矩阵 grid 。
第 2 个图表示对单元格 (0,0) 计算,其中蓝色单元格是位于右下对角线的单元格。
第 3 个图表示对单元格 (1,2) 计算,其中红色单元格是位于左上对角线的单元格。
第 4 个图表示对单元格 (1,1) 计算,其中蓝色单元格是位于右下对角线的单元格,红色单元格是位于左上对角线的单元格。
- 单元格 (0,0) 的右下对角线包含 [1,1] ,而左上对角线包含 [] 。对应答案是 |1 - 0| = 1 。
- 单元格 (1,2) 的右下对角线包含 [] ,而左上对角线包含 [2] 。对应答案是 |0 - 1| = 1 。
- 单元格 (1,1) 的右下对角线包含 [1] ,而左上对角线包含 [1] 。对应答案是 |1 - 1| = 0 。
其他单元格的对应答案也可以按照这样的流程进行计算。
示例 2:
输入:grid = [[1]]
输出:[[0]]
解释:- 单元格 (0,0) 的右下对角线包含 [] ,左上对角线包含 [] 。对应答案是 |0 - 0| = 0 。
提示:
m == grid.lengthn == grid[i].length1 <= m, n, grid[i][j] <= 50
思路
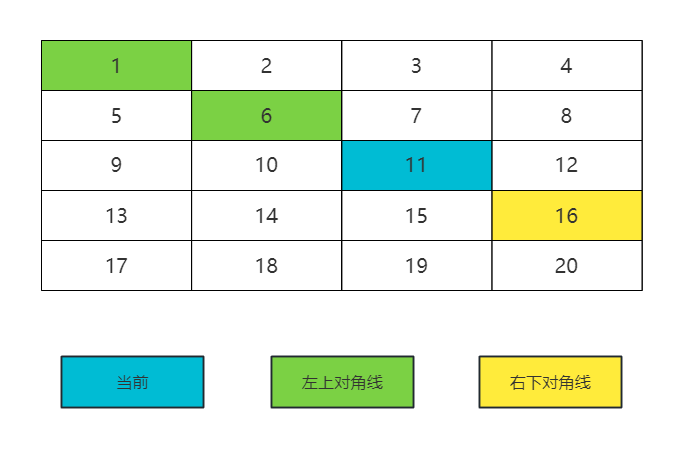
先读懂题目,这里的矩阵对角线仅仅是指,左上方到右下角这个方向的对角线。如果当前位置坐标是(i, j),左上对角线是指 (i-1, j-1)、(i-2, j-2)、 (i-3, j-3)、... 这些位置的连线,右下对焦线只是 (i+1, j+1)、(i+2, j+2)、(i+3, j+3)、... 这些位置的连线。左上对角线和右上对角线都不包含当前节点。
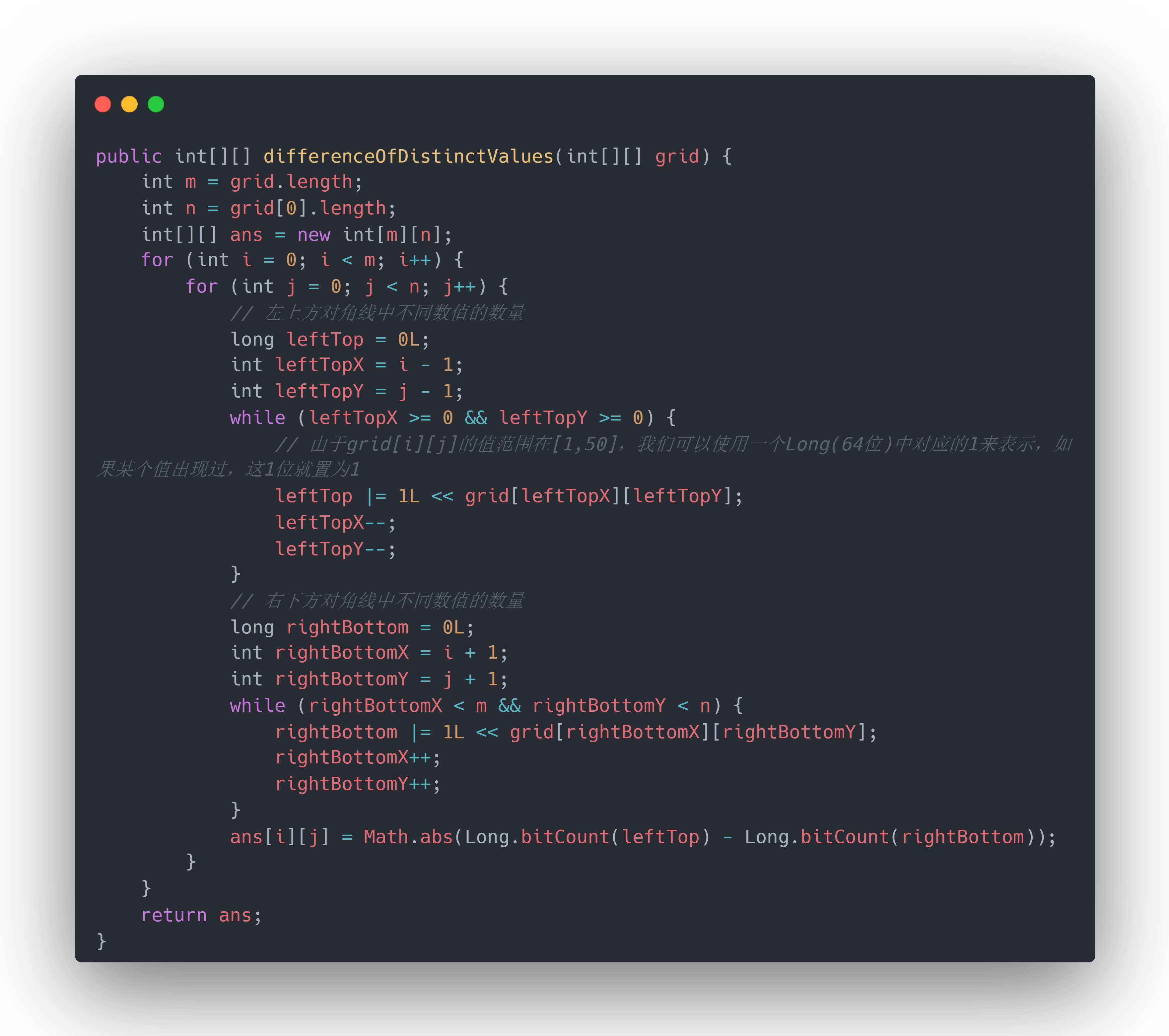
读懂题意后,可以直接模拟,遍历二维数组的每个位置,然后求出这个位置左上角和右下角对角线中不同数值的数量。这里不同值最直观的方法是直接用Set去重。不过注意到值范围[1, 50]很小,我们可以用bitmap的思路,用一个Long类型(64位)的值来存,如果某个值 x 出现,就把从右开始第x位置为1,那么最后不同值的数量就是这个Long值的二进制表示中,1的数量。
图解
代码
优化
上述直接模拟的方法中,对于同一条对角线,遍历到对角线上每一个位置的时候,都被计算了一遍,存在浪费。我们在遍历二维数组的时候,可以不按照传统的行和列来遍历,而是按照对角线来遍历。对于同一条对角线的位置,我们不难发现 i - j 的值都是相等的,所以我们可以使用 i-j 来记录1条对角线。这条对角线的位置就形成了1个1维数组,我们只需要从前往后、从后往前各遍历1次,就可以得到每个位置左上和右下部分不同值的数量了。
优化后代码
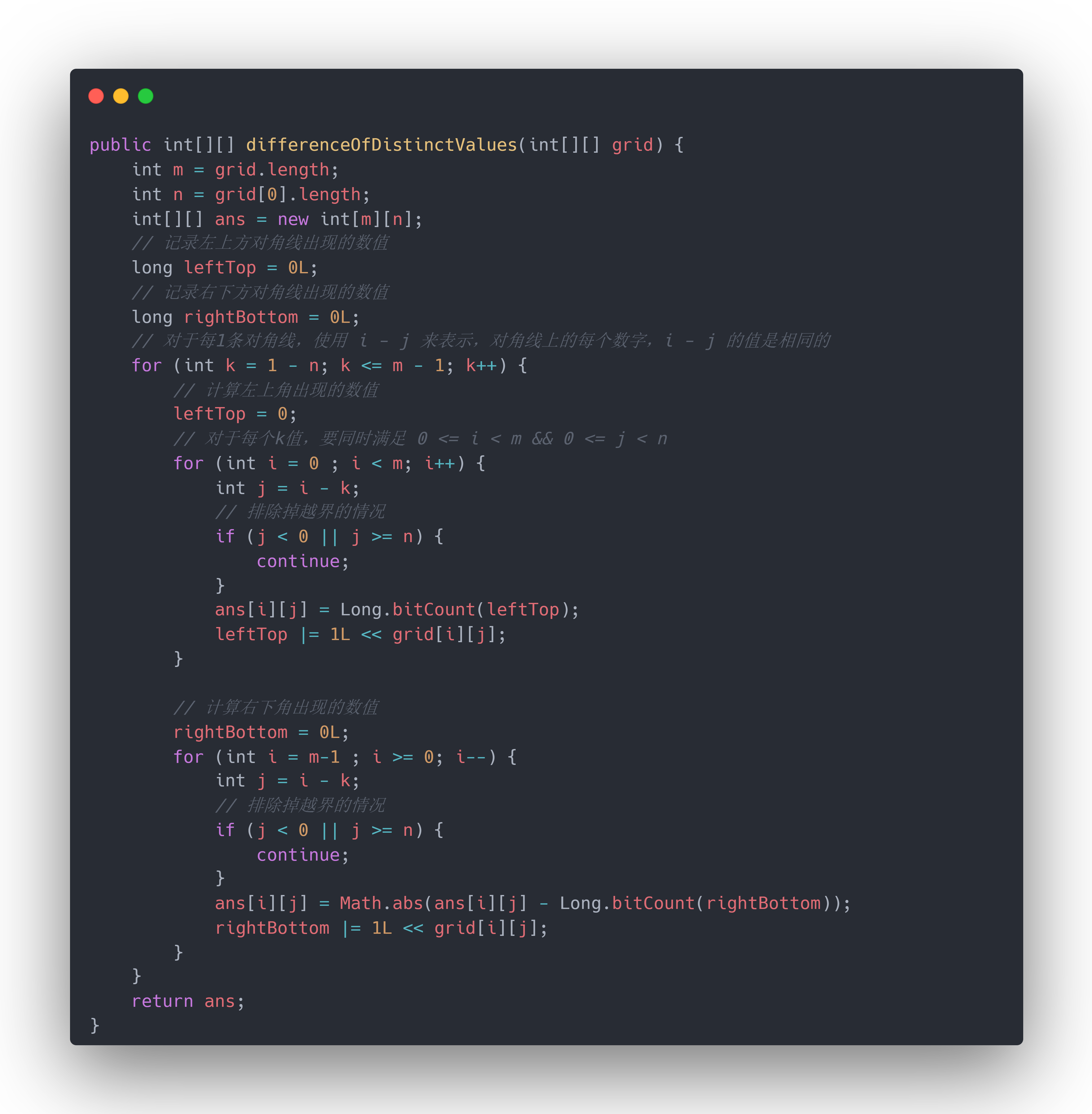
public int[][] differenceOfDistinctValues(int[][] grid) {int m = grid.length;int n = grid[0].length;int[][] ans = new int[m][n];// 记录左上方对角线出现的数值long leftTop = 0L;// 记录右下方对角线出现的数值long rightBottom = 0L;// 对于每1条对角线,使用 i - j 来表示,对角线上的每个数字,i - j 的值是相同的for (int k = 1 - n; k <= m - 1; k++) {// 计算左上角出现的数值leftTop = 0;// 对于每个k值,要同时满足 0 <= i < m && 0 <= j < nfor (int i = 0 ; i < m; i++) {int j = i - k;// 排除掉越界的情况if (j < 0 || j >= n) {continue;}ans[i][j] = Long.bitCount(leftTop);leftTop |= 1L << grid[i][j];}// 计算右下角出现的数值rightBottom = 0L;for (int i = m-1 ; i >= 0; i--) {int j = i - k;// 排除掉越界的情况if (j < 0 || j >= n) {continue;}ans[i][j] = Math.abs(ans[i][j] - Long.bitCount(rightBottom));rightBottom |= 1L << grid[i][j];}}return ans;
}
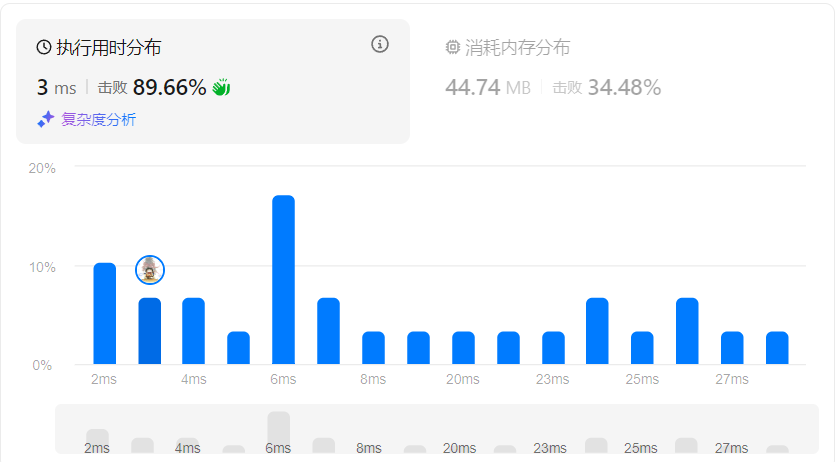
耗时