树链剖分-重链剖分

树链剖分-重链剖分

前置知识

树形结构，链式前向星，线段树，DFS序，LCA

定义

树链剖分（树剖）：将树分解为一条条不相交的，从祖先到孙子的链。

第零部分：建树与基本概念

建树：给定\(n\)个节点用链式前向星（或邻接表）建树

基本概念：

1. 重儿子：假设\(x\)有\(n\)个儿子节点，其中以\(i\)儿子节点的为根子树大小最大，\(i\)就是\(x\)的重儿子
2. 轻儿子：除重儿子外的所有儿子均为轻儿子
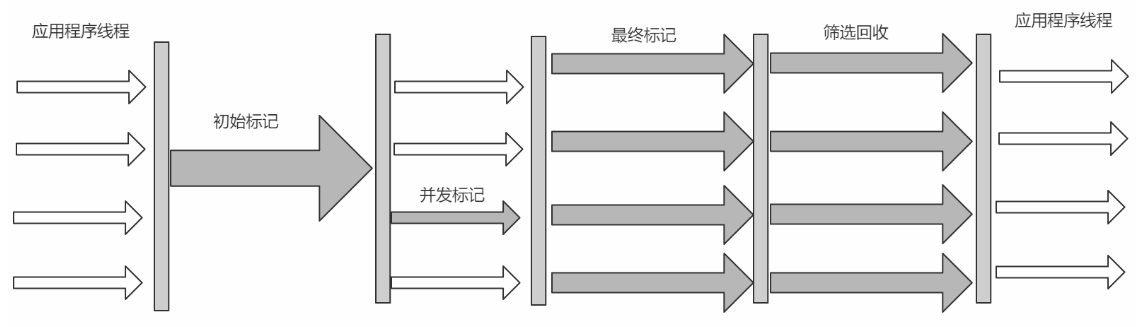
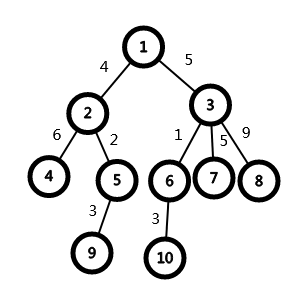
   以上图为例
   \(1\)的重儿子为\(3\)，轻儿子为\(2\)
   \(3\)的重儿子为\(6\)，其余的为轻儿子
3. 轻边：\(x\)与轻儿子相连的边
4. 重边：\(x\)与重儿子相连的边
5. 轻链：均由轻儿子构成的一条链
6. 重链：均由重儿子构成的一条链

第一部分：对表示节点信息的数组进行预处理

定义以下数组：

1. \(d[x]\) 表示节点\(x\)的深度
2. \(fa[x]\) 表示节点\(x\)的父亲节点
3. \(son[x]\) 表示节点\(x\)的重儿子
4. \(siz[x]\) 表示以节点\(x\)为根的子树大小
5. \(top[x]\) 表示节点\(x\)所在重链的顶点

第一次DFS

数组\(d\)、\(fa\)、\(son\)均可用DFS很方便的求出，而\(siz\)数组则用到了DFS序的思想（详见《算法竞赛进阶指南》第\(0x21\)节）

void DFS1(int now，int dad）//now 为当前节点编号，dad 为其父节点编号
{fa[now] = dad;//记录父节点siz[now] = 1;//子树应算上根节点nowson[now] = 0;//求重儿子的过程涉及到比较//这里是将节点now的重儿子编号赋为0//故以其重儿子为根的子树大小为0（即不存在）d[now] = d[dad] + 1;for(int i = head[now]; i; i = edge[i].Next){if(edge[i].to == dad)//对树进行dfs，故不访问父节点continue;DFS1(edge[i].to, now);siz[son] += siz[edge[i].to];//以一个节点为根的树（子树）的大小//就是所有以其儿子节点为根的子树的大小之和+1if(siz[son[now]] < siz[edge[i].to])son[now] = edge[i].io;//更新重儿子}
}

第二次DFS

现在还剩下\(top\)数组没有求，第二次DFS的目的便是将其求出

1. 对于一个节点的重儿子而言
   这个重儿子节点肯定在一条重链上，该链的顶点必定是其祖宗
2. 对于一个节点的轻儿子而言
   这个轻儿子节点所在重链的顶点便是其本身（即新剖一条链），因为包含其父节点所在重链中其父节点的后继便是其父节点的重儿子，而非轻儿子

为了记录一个节点的重儿子对应的\(top\)值，故必须记录该重儿子所在链的顶点。

void DFS2(int now,int Top)
{
//Top即上文提到的重儿子所在链的顶点，因此now也就是其父节点的重儿子
//或者是以一个节点的轻儿子为顶点的链，now便是该节点，Top也是top[now] = Top;if(son[now])//叶节点没有儿子DFS2(son[now], Top);//继续链接重链elsereturn;//now是叶节点for(int i = head[now]; i; i = edge[i].Next)//处理轻儿子{if(edge[i].to != fa[now] && edge[i].to != son[now])//轻儿子肯定不是父亲，也不是重儿子DFS2(edge.[i].to, edge[i].to);//新剖一条以该轻儿子为顶点的链}
}