交换排序--冒泡排序和快速排序-编程知识

交换，是指根据序列中两个元素关键字的比较结果来对换这两个记录在序列中的位置

一，冒泡排序

1.基本思想：从后往前（或从前往后）两两比较相邻元素的值，若为逆序（A[i-1] > A[i]），则交换它们，直到序列比较完

2.过程

数组序号	0	1	2	3	4	5	6	7
待排序元素	49	38	65	97	76	13	27	49
49和27比较	49	38	65	97	76	13	27	49
27和13比较	49	38	65	97	76	13	27	49
13和76比较	49	38	65	97	13	76	27	49
13和97比较	49	38	65	13	97	76	27	49
13和65比较	49	38	13	65	97	76	27	49
13和38比较	49	13	38	65	97	76	27	49
13和49比较	13	49	38	65	97	76	27	49

冒泡排序中所产生的有序子序列一定是全局有序的（不同于直接插入排序），也就是说，有序子序列中的所有元素的关键字一定小于（或大于）无序子序列中所有元素的关键字，这样每趟排序都会将一个元素放置到最终的位置上

3.代码展示

//冒泡排序
void BubbleSort(Str &L)
{for(int i = 0; i < L.length-1; ++i)//i表示的是i前面有几个已经确定好最终位置的元素{bool flag = false;//表示本次冒泡是否发生交换的标志for(int j = L.length-1; j > i; --j)//从待排序列最后一个元素依次向前进行比较，已经排好的元素无需再比较，所以是j > i{if(L.data[j] < L.data[j-1])//元素是从小到大的顺序进行排序{swap(L.data[j],L.data[j-1]);//交换位置flag = true;//表示这趟冒泡过程发生了交换}	}if(flag == false)//如果没有发生交换，就表示待排序列已经排序好了，直接结束程序return;}
}

4.结果:

二，快速排序

1.基本思想：在待排序表L[1....n]中任取一个元素pivot作为枢轴（或称基准，通常取首元素），通过排序将排序表分为两部分，L[1...k-1]中元素小于pivot,L[k+1...n]元素大于等于pivot,最后将pivot元素放到L[k]中，直到所有元素全部放到最终位置。

2.过程

2.1,将序号low元素作为枢轴放到pivot中

数组序号	0	1	2	3	4	5	6	7
待排序列	49	38	65	97	76	13	27	49
	low							high

2.2，此时序号low中的元素已经被赋值到其他变量中，所以此时序号low可以被赋值其他值，所以要从high开始访问。因为49>=49,所以high = high-1 = 6; 27<49,所以将27赋值到序号low处。

数组序号	0	1	2	3	4	5	6	7
待排序列	27	38	65	97	76	13	27	49
	low						high

2.3,此时原本序号6中的元素以及被赋值到0处，所以序号6处的元素可以被覆盖，所以从low开始进行访问。27<49,low = low+1 = 1; 38<49,low = low+1 = 2; 65>49,所以将65赋值到high处

数组序号	0	1	2	3	4	5	6	7
待排序列	27	38	65	97	76	13	65	49
			low				high

2.4,同理，65>49, high = high-1 = 5; 13<49,将13赋值到low处。

数组序号	0	1	2	3	4	5	6	7
待排序列	27	38	13	97	76	13	65	49
			low			high

2.5，同理，13<49,low = low+1 = 3; 97>49,所以将97赋值到high处

数组序号	0	1	2	3	4	5	6	7
待排序列	27	38	13	97	76	97	65	49
				low		high

2.6，同理，97>49,high = high-1 = 4; 76>49, high = high-1 = 3; 此时high = low = 3,所以将49赋值到low处

数组序号

待排序列

low

high

在快速排序算法中，并不产生有序子序列，但每趟排序之后会将上一趟划分的各个无序子表的枢轴（基准）元素放到其最终的位置上

408原题中说，对所有尚未确定最终位置的所有元素进行一遍处理称为“一趟”排序，因此依次“划分”！= “一趟排序”。一次划分可以确定一个元素最终的位置，二一趟排序也许可以确定多个元素的最终位置

3.代码展示

//快速排序
void QuickSort(Str &L,int low, int high)
{//类似于二叉树，进行递归if(low < high){int pivotpos = Partition(L,low,high);//划分操作，以low所在序号元素作为枢轴元素，将待排序列划分成左边是比枢轴元素小，右边比枢轴元素大QuickSort(L,low,pivotpos-1);//依次对两个子表进行划分，进行递归QuickSort(L,pivotpos+1,high);}
}int Partition(Str &L,int low, int high)
{int pivot = L.data[low];//将low所在序号元素作为枢轴，暂存在pivot里面，以免被覆盖while(low < high)//循环条件{while(low < high && L.data[high] >= pivot)//最开始已经将序号为low的数组元素已经赋值给其他变量中，所以现在low序号的元素可以被覆盖，所以是从high那边开始high--;//如果L.data[high] > pivot，就符合要求，这就检查前面那个元素，所以high--;L.data[low] = L.data[high];//如果不满足条件low < high，那就是high = low，此时L.data[low] = L.data[high]，不会有影响；如果L.data[high] < pivot,那就将元素赋值到序号low中while(low < high && L.data[low] < pivot)//如果满足条件那么就向后面一个元素进行访问low++;L.data[high] = L.data[low];//如果不满足条件，这个1时候序号high所在数组元素已经赋值给其他地方，此时覆盖不会造成元素丢失}L.data[low] = pivot;//结束循环，找到枢轴所在位置，将pivot中元素赋值到该位置，就可以达到左边比其小，右边比其大return low;//返回存放枢轴的最终位置
}

4.结果

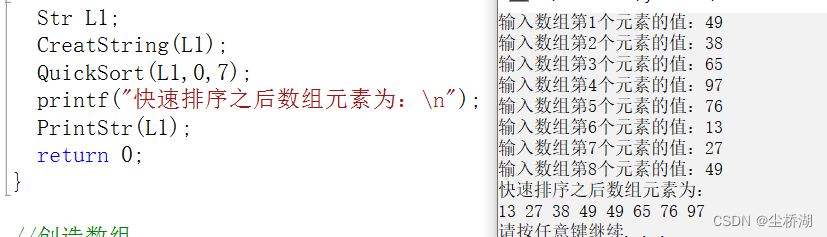
三，总结

交换排序	空间复杂度	时间复杂度	稳定性
冒泡排序	O(1)	O( $n^{2}$ )	稳定
快速排序	O(递归层数)	O(n*递归层数)	不稳定

最好情况：若每一次选中的枢轴将待排序列划分成均匀的两个部分，则递归深度最小，算法效率最高。类似于二叉树，n个结点的二叉树最小高度 = $\log n$ +1

空间复杂度最好情况为：O( $\log n$ ); 时间复杂度最好情况为：O(n $\log n$ )

最坏情况：n个结点二叉树最大高度为n

空间复杂度最坏情况为：O(n); 时间复杂度最坏情况为：O( $n^{2}$ )

一般情况下，最坏的情况几率比较小，所以快速排序平均时间复杂度为O(n $\log n$ )

快速排序是所有内部排序算法中平均性能最优的排序算法

交换排序	元素是否被放在最终位置上
冒泡排序	产生的有序子序列一定是全局有序的（不同于直接插入排序），也就是说，有序子序列中的所有元素的关键字一定小于（或大于）无序子序列中所有元素的关键字，这样每趟排序都会将一个元素放置到最终的位置上
快速排序	在快速排序算法中，并不产生有序子序列，但每趟排序之后会将上一趟划分的各个无序子表的枢轴（基准）元素放到其最终的位置上

四，完整代码

#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>
#define Maxsize 8
//数组结构体
typedef struct
{int *data;int length;
}Str;//函数说明
void CreatString(Str &L);
void swap(int &a, int &b);
void BubbleSort(Str &L);
void PrintStr(Str L);
void QuickSort(Str &L,int low, int high);
int Partition(Str &L,int low, int high);int main(void)
{Str L;CreatString(L);BubbleSort(L);printf("冒泡排序之后数组元素为：\n");PrintStr(L);Str L1;CreatString(L1);QuickSort(L1,0,7);printf("快速排序之后数组元素为：\n");PrintStr(L1);return 0;
}//创造数组
void CreatString(Str &L)
{L.data = (int *)malloc(sizeof(int)*Maxsize);L.length = Maxsize;int val;for(int i = 0; i < L.length; ++i){printf("输入数组第%d个元素的值：",i+1);scanf_s("%d",&val);L.data[i] = val;}
}//交换函数
void swap(int &a, int &b)
{int temp = a;a = b;b = temp;
}//冒泡排序
void BubbleSort(Str &L)
{for(int i = 0; i < L.length-1; ++i)//i表示的是i前面有几个已经确定好最终位置的元素{bool flag = false;//表示本次冒泡是否发生交换的标志for(int j = L.length-1; j > i; --j)//从待排序列最后一个元素依次向前进行比较，已经排好的元素无需再比较，所以是j > i{if(L.data[j] < L.data[j-1])//元素是从小到大的顺序进行排序{swap(L.data[j],L.data[j-1]);//交换位置flag = true;//表示这趟冒泡过程发生了交换}	}if(flag == false)//如果没有发生交换，就表示待排序列已经排序好了，直接结束程序return;}
}//遍历输出
void PrintStr(Str L)
{for(int i = 0; i < L.length; ++i){printf("%d ",L.data[i]);}printf("\n");
}//快速排序
void QuickSort(Str &L,int low, int high)
{//类似于二叉树，进行递归if(low < high){int pivotpos = Partition(L,low,high);//划分操作，以low所在序号元素作为枢轴元素，将待排序列划分成左边是比枢轴元素小，右边比枢轴元素大QuickSort(L,low,pivotpos-1);//依次对两个子表进行划分，进行递归QuickSort(L,pivotpos+1,high);}
}int Partition(Str &L,int low, int high)
{int pivot = L.data[low];//将low所在序号元素作为枢轴，暂存在pivot里面，以免被覆盖while(low < high)//循环条件{while(low < high && L.data[high] >= pivot)//最开始已经将序号为low的数组元素已经赋值给其他变量中，所以现在low序号的元素可以被覆盖，所以是从high那边开始high--;//如果L.data[high] > pivot，就符合要求，这就检查前面那个元素，所以high--;L.data[low] = L.data[high];//如果不满足条件low < high，那就是high = low，此时L.data[low] = L.data[high]，不会有影响；如果L.data[high] < pivot,那就将元素赋值到序号low中while(low < high && L.data[low] < pivot)//如果满足条件那么就向后面一个元素进行访问low++;L.data[high] = L.data[low];//如果不满足条件，这个1时候序号high所在数组元素已经赋值给其他地方，此时覆盖不会造成元素丢失}L.data[low] = pivot;//结束循环，找到枢轴所在位置，将pivot中元素赋值到该位置，就可以达到左边比其小，右边比其大return low;//返回存放枢轴的最终位置
}