1. 线段树分裂
【模板】线段树分裂
https://www.gxyzoj.com/d/gxyznoi/p/P223
采用和平衡树一样的方法,先求和,然后按线段树二分的写法即可
点击查看代码
#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;
const int N=2e5+5,M=4e6+5;
int n,m,ls[M],del[M],rs[M],rt[N],tot,cnt=1,dcnt;
ll val[M];
int newnode()
{if(dcnt) return del[dcnt--];return ++tot;
}
int update(int p,int l,int r,int x,ll v)
{if(!p) p=newnode();if(l==r){val[p]+=v;return p;}int mid=(l+r)>>1;if(x<=mid) ls[p]=update(ls[p],l,mid,x,v);else rs[p]=update(rs[p],mid+1,r,x,v);val[p]=val[ls[p]]+val[rs[p]];return p;
}
ll query(int p,int l,int r,int ql,int qr)
{if(!p) return 0;if(ql<=l&&qr>=r){return val[p];}int mid=(l+r)>>1;ll x=0;if(ql<=mid) x+=query(ls[p],l,mid,ql,qr);if(qr>mid) x+=query(rs[p],mid+1,r,ql,qr);return x;
}
void split(int x,int &y,ll k)
{if(!x) return;y=newnode();ll v=val[ls[x]];if(k>v) split(rs[x],rs[y],k-v);else swap(rs[x],rs[y]);if(k<v) split(ls[x],ls[y],k);val[y]=val[x]-k;val[x]=k;
}
void delt(int x)
{del[++dcnt]=x;val[x]=ls[x]=rs[x]=0;
}
int merge(int x,int y)
{if(!x||!y) return x+y;val[x]+=val[y];ls[x]=merge(ls[x],ls[y]);rs[x]=merge(rs[x],rs[y]);delt(y);return x;
}
int getans(int p,int l,int r,ll k)
{if(l==r) return l;int mid=(l+r)>>1;if(k<=val[ls[p]]) return getans(ls[p],l,mid,k);else return getans(rs[p],mid+1,r,k-val[ls[p]]);
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){int x;scanf("%d",&x);if(x) rt[1]=update(rt[1],1,n,i,x);}while(m--){int opt,p,a=0;ll l,r;scanf("%d%d%lld",&opt,&p,&l);if(opt==0){scanf("%lld",&r);++cnt;ll k1=query(rt[p],1,n,1,r),k2=query(rt[p],1,n,l,r);split(rt[p],rt[cnt],k1-k2);split(rt[cnt],a,k2);rt[p]=merge(rt[p],a);}if(opt==1){rt[p]=merge(rt[p],rt[l]);}if(opt==2){scanf("%lld",&r);rt[p]=update(rt[p],1,n,r,l);}if(opt==3){scanf("%lld",&r);printf("%lld\n",query(rt[p],1,n,l,r));}if(opt==4){if(query(rt[p],1,n,1,n)<l){printf("-1\n");continue;}printf("%d\n",getans(rt[p],1,n,l));}}return 0;
}


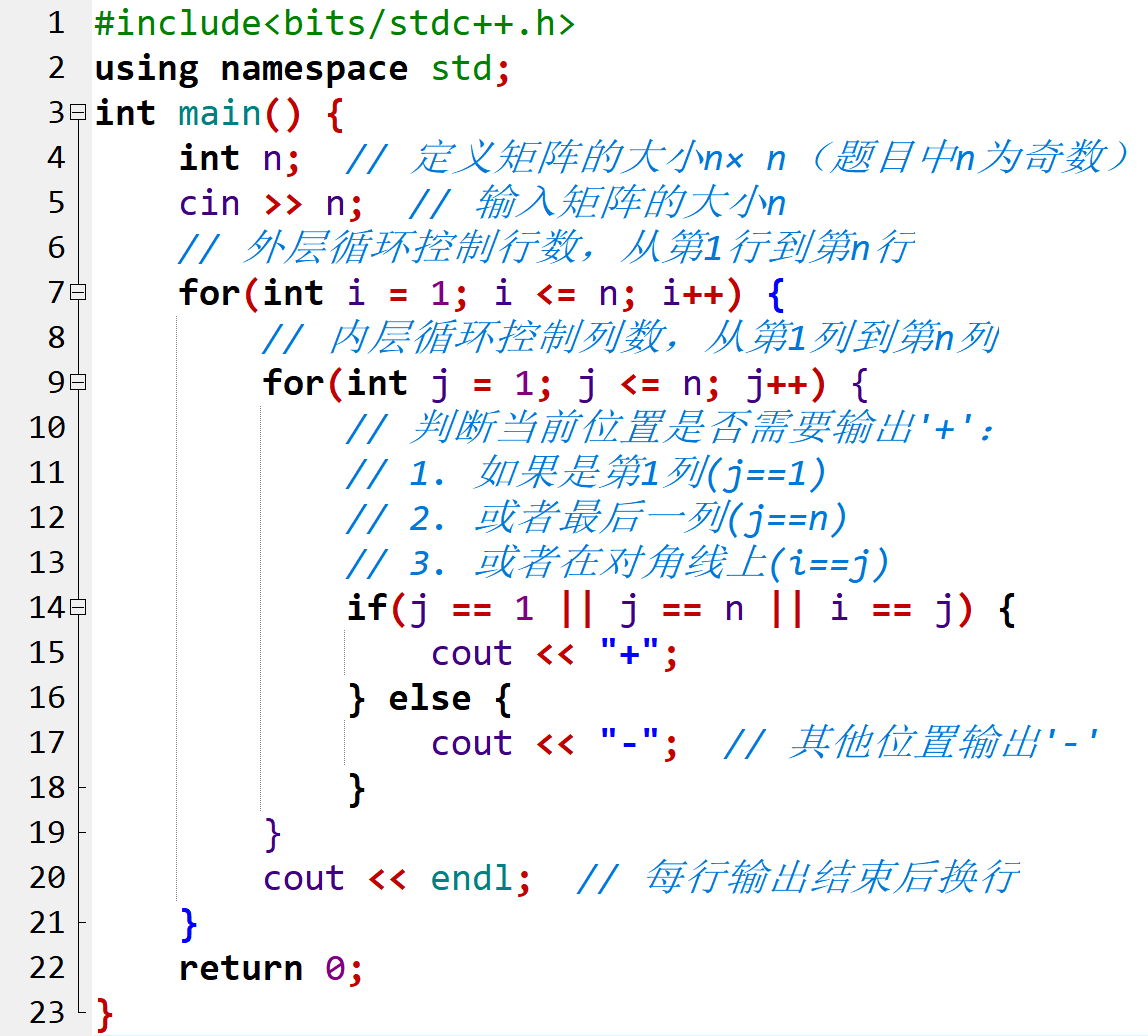


![B4007 [GESP202406 二级] 计数](https://img2024.cnblogs.com/blog/2727880/202503/2727880-20250326202019619-1954691428.png)
