每天刷个一两题 比较值得写的会写在这里
P6464 [传智杯 #2 决赛] 传送门
题目描述
传智专修学院里有 \(n\) 栋教学楼,有 \(m\) 条双向通行道路连接这些教学楼,不存在重边和自环。每条道路都有一定的长度,而且所有教学楼之间都可以直接或者间接的通过道路到达。我们可以很容易的求出这些教学楼之间的最短路。
为了使交通更为顺畅,校方决定在两个教学楼里增设一对传送门。传送门可以将这对教学楼的距离直接缩短为 0。利用传送门,某些教学楼之间的最短路的距离就变短了。
由于预算有限,学校里只能安装一对传送门。但是校长希望尽可能方便学生,使任意两点之间的最短路长度的总和最小。当然啦,从 \(x\) 教学楼到 \(y\) 教学楼的长度和从 \(y\) 教学楼到 \(x\) 教学楼的长度只需要统计一次就可以了。
输入格式
输入第 1 行两个正整数 \(n,m(n\le 100,m\le\frac{1}{2}n(n-1))\),代表教学楼和道路数量。
接下来 \(m\) 行,每行三个正整数 \(x_i,y_i,w_i(0 <w_i \le 10^4)\),表示在教学楼 \(x_i\) 和 \(y_i\) 之间,有一条长度为 \(w_i\) 的道路。
输出格式
输出一行,在最优方案下的任意点对的最短道路之和。
输入输出样例 #1
输入 #1
4 5
1 2 3
1 3 6
2 3 4
2 4 7
3 4 2
输出 #1
14
说明/提示
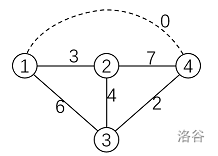
样例如图。当在 1 和 4 号教学楼架设一对传送门时,1 → 2 的最短路是 3,1 → 3 的最短路是 0+2,1 → 4 的最短路是 0,2 → 3 的最短路是 4,2 → 4 的最短路是 3+0,3 → 4 的最短路是 2,最短路之和是 14,是最佳方案。
解法&&个人感想
我们看到这个数据范围\(n<=100\)肯定是要用Floyd算法的 但是如果一一枚举传送门的话就会变成\(n^5\) 这个时间复杂度我们接受不了
所以 怎么办?
我们考虑上次看到的那个中转点思想 先跑一遍Floyd 然后枚举\(n^2\)的点对x,y作为传送门 对于最短路的两个起始点i,j,其距离被更新为原来最小值,i到x+y到j,i到y加x到j这三个的最小值,就将算法优化到\(n^4\)了
下面我们看代码:
#include<bits/stdc++.h>
#define MAXN 105
#define MAXM 1e4+5
#define INF 1e8
#define ll long long
using namespace std;
int n,m;
int x,y,z;
int ma[MAXN][MAXN];
int tem[MAXN][MAXN];
ll res=INF;
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){ma[i][j]=INF;}}for(int i=1;i<=n;i++) ma[i][i]=0;for(int i=1;i<=m;i++){scanf("%d%d%d",&x,&y,&z);ma[x][y]=z;ma[y][x]=z;}for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){ma[i][j]=min(ma[i][j],ma[i][k]+ma[k][j]);}}}for(int i=1;i<=n;i++){for(int j=i+1;j<=n;j++){ll ans=0;for(int k=1;k<=n;k++){for(int v=1;v<=n;v++){tem[k][v]=ma[k][v];}}for(int k=1;k<=n;k++){for(int v=1;v<=n;v++){tem[k][v]=min(tem[k][v],min(tem[k][i]+tem[j][v],tem[k][j]+tem[i][v]));}}for(int k=1;k<=n;k++){for(int v=k+1;v<=n;v++){ans+=tem[k][v];}}res=min(res,ans);}}printf("%lld",res);system("pause");return 0;
}