here.
挺有意思的一场,但是我真不会 F2。
D
考虑把这个过程反过来,从后往前做,题意转化为每次进行两次操作中的一个:
-
\(r \to r+1\);
-
\(r \to r-k,ans\to ans+d_i\)
你发现这是一个经典的反悔贪心模型。
考虑用小根堆维护目前选择的 \(d_i\),然后每次能选就选,不能选考虑用之前的最小值尝试替换。
复杂度 \(O(n \log n)\)。
#include<bits/stdc++.h>
#define int long long
using namespace std;
int t,n,k,ans,cnt,a[2000005];
priority_queue<int,vector<int>,greater<int> > q;
signed main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>t;while(t--){cin>>n>>k;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=n;i>=1;i--){if(cnt<k){if(q.size() && q.top()<a[i]){q.pop();q.push(a[i]);}cnt++;}else{cnt-=k;q.push(a[i]);}}ans=cnt=0;while(q.size()){ans+=q.top();q.pop();}cout<<ans<<'\n';}return 0;
}
E
纯种诈骗题不是。
考虑两个序列的和做差,记为 \(d\),一定是 \(k\) 的倍数。
然后枚举 \(d\) 的所有因数,暴力检查它们是不是合法的 \(k\)。
注意 \(d=0\) 时,因为 \(0\) 是所有数的倍数,所以我们直接检查 \(10^9\) 是否合法就行。
复杂度 \(O(能过)\)。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int inf=1e9;
int t,n,a[200005],b[200005],c[200005],suma,sumb,k,ans;
bool check(int k){if(k>inf) return false;for(int i=1;i<=n;i++){c[i]=a[i]%k;}sort(c+1,c+1+n);for(int i=1;i<=n;i++){if(b[i]!=c[i]) return false;}return true;
}
signed main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>t;while(t--){cin>>n;for(int i=1;i<=n;i++){cin>>a[i];suma+=a[i];}for(int i=1;i<=n;i++){cin>>b[i];sumb+=b[i];}sort(b+1,b+1+n);k=suma-sumb;if(k<0){cout<<-1<<'\n';}else{if(!k && check(inf)) ans=inf;for(int i=1;i*i<=k;i++){if(k%i==0){if(check(k/i)){ans=k/i;break;}else if(check(i)){ans=i;break;}} }if(ans) cout<<ans<<'\n';else cout<<-1<<'\n';}suma=sumb=k=ans=0;}return 0;
}
F1
考虑这个移动的过程,相当于在序列中每个颜色选择一个位置,然后让它们向中间靠拢,形成一段连续的区间。
考虑枚举区间和区间中点,我们希望每个颜色选择距离中点最近的一个,这个选择的过程也可以循环找出。
找出所有位置后,把它们排序,依次匹配 \([l,r]\) 中的点。
然后就做完了,复杂度 \(O(n^2 \log n)\)。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int inf=1e18;
int t,n,k,ans,sum,a[3005],pos[3005];
signed main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>t;while(t--){cin>>n>>k;for(int i=1;i<=n;i++){cin>>a[i];}ans=inf;for(int l=1,r=k,mid=(l+r)>>1;r<=n;l++,r++,mid++){memset(pos,-1,sizeof(pos));pos[a[mid]]=mid;for(int i=1;i<=n;i++){if(mid-i>=1 && pos[a[mid-i]]==-1) pos[a[mid-i]]=mid-i;if(mid+i<=n && pos[a[mid+i]]==-1) pos[a[mid+i]]=mid+i;}sum=0;sort(pos+1,pos+1+k);for(int i=l;i<=r;i++){sum+=abs(pos[i-l+1]-i);}ans=min(ans,sum);}cout<<ans<<'\n';}
}
F2
考虑上面那个做法实在是太朴素了,能不能加点合并处理的部分。
首先我们把区间中点左边第一个遇到颜色为 \(i\) 的位置记为 \(l_i\),区间右边第一个遇到颜色为 \(i\) 的位置记为 \(r_i\)。
那么实际上我们求的是 \(\sum_{i=1}^{k} \min(l_i,r_i)\)。
考虑区间中点每次右移一位,\(\min(l_i,r_i)\) 只会 \(+1,-1\) 或者不变,具体地,设颜色 \(i\) 两次相邻出现的位置是 \(a,b\),那么当区间中点在 \(\frac{a+b}{2}\) 左侧时,移动一位增加 \(1\),在 \(\frac{a+b}{2}\) 右侧时,移动一位减少 \(1\),注意判断 \((a+b)\) 是奇数的情况。
然后其实可以差分求出贡献的,然后就做完了,但是实现上细节太多并不是很好调。
复杂度 \(O(n)\)。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int inf=1e18;
int t,n,k,s,d,ans,a[400005],lst[400005],sum[400005];
signed main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>t;while(t--){cin>>n>>k;ans=inf;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n;i++){lst[a[i]]=sum[i]=0;}s=d=0;for(int i=1;i<=n;i++){if(!lst[a[i]]){s+=i-1;}else{int pre=lst[a[i]],mid=(pre+i)>>1;if((pre+i)&1) sum[mid]--,sum[mid+1]--;else sum[mid]-=2;}sum[i]+=2;lst[a[i]]=i;}d=-k;for(int i=1;i<=n;i++){ans=min(ans,s);d+=sum[i];s+=d;}for(int i=1;i<=k;i++){ans-=abs((k+1)/2-i);}cout<<ans<<'\n';}return 0;
}
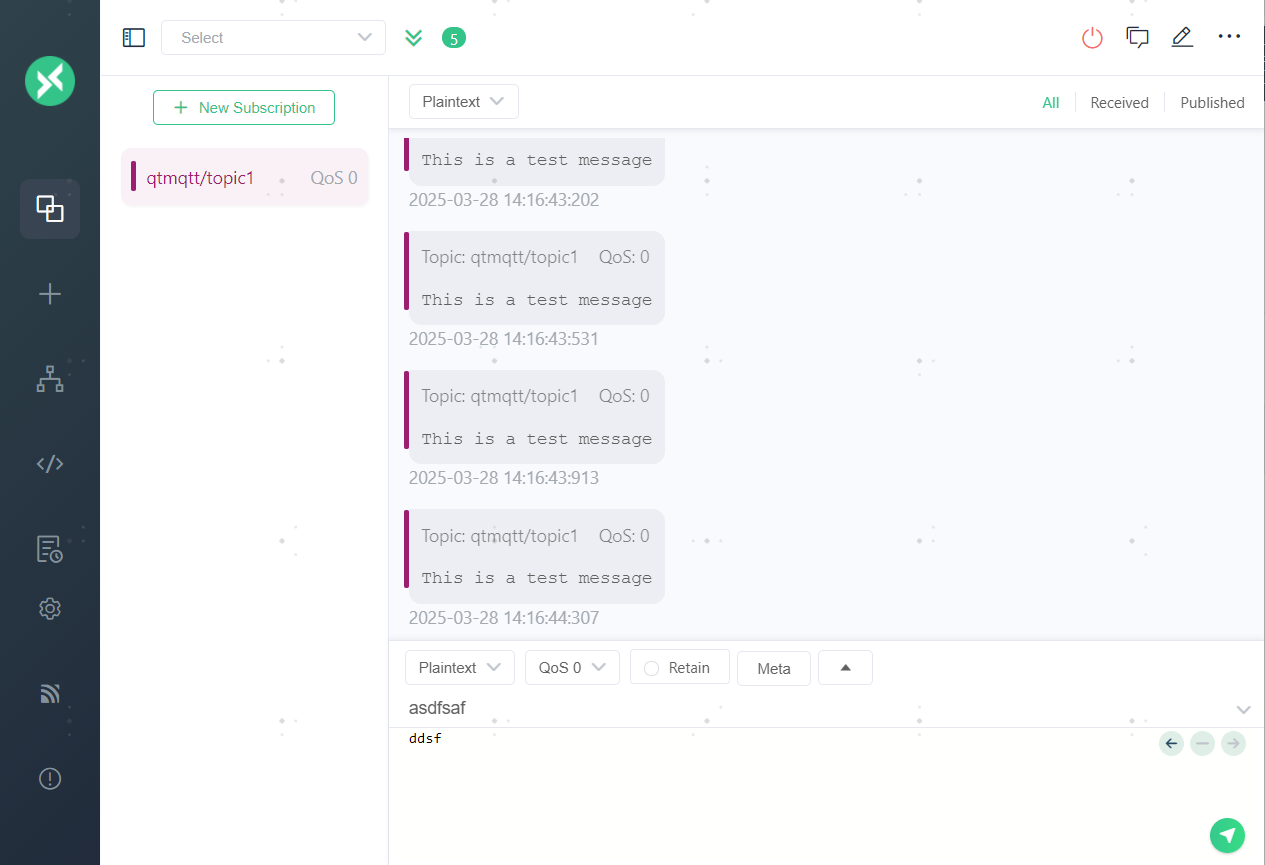
![B3708 [语言月赛202302] 神树大人挥动魔杖](https://img2024.cnblogs.com/blog/3619440/202503/3619440-20250328141952449-312541226.png)
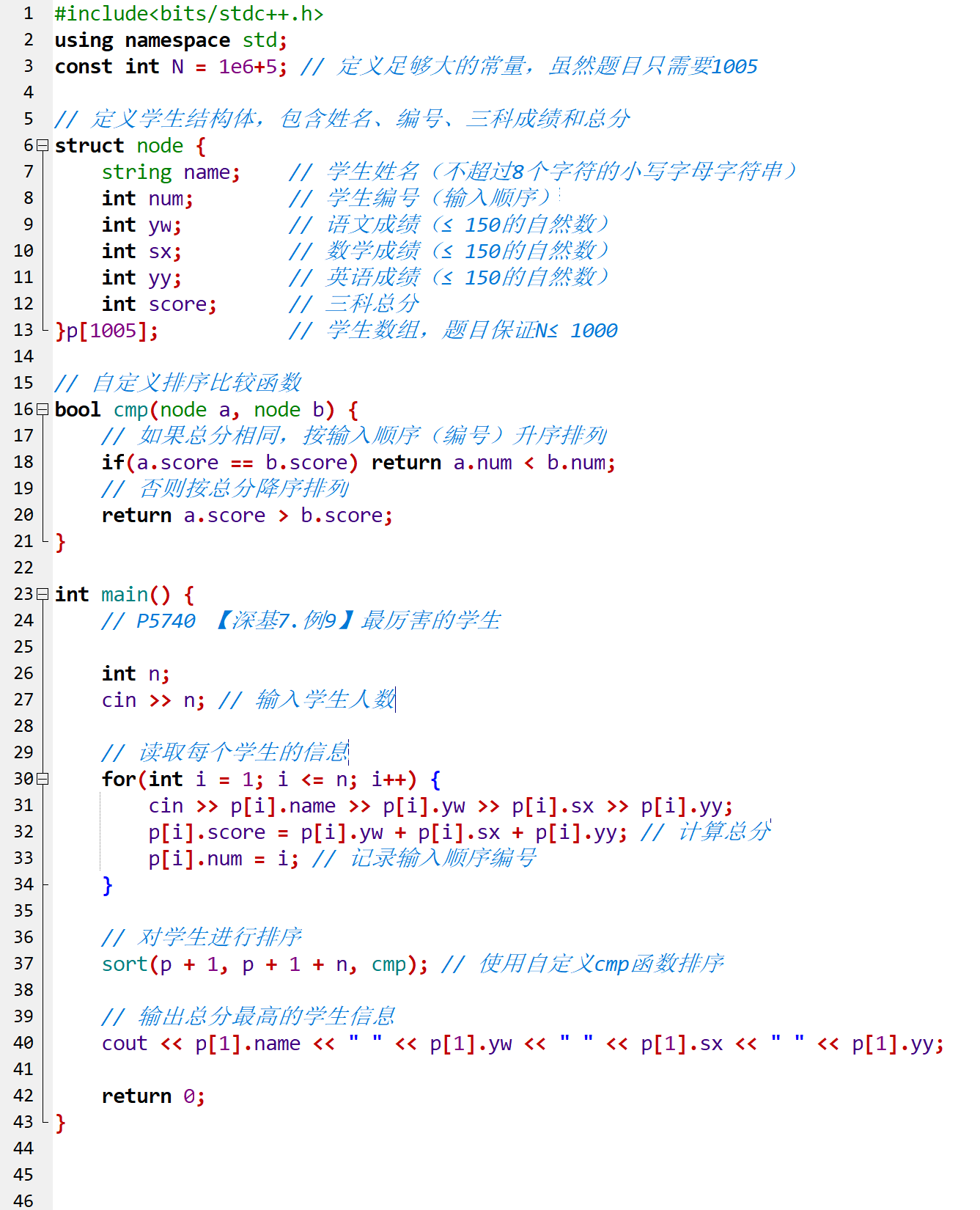

![P1059 [NOIP 2006 普及组] 明明的随机数](https://img2024.cnblogs.com/blog/3619440/202503/3619440-20250328141002789-1043756064.png)