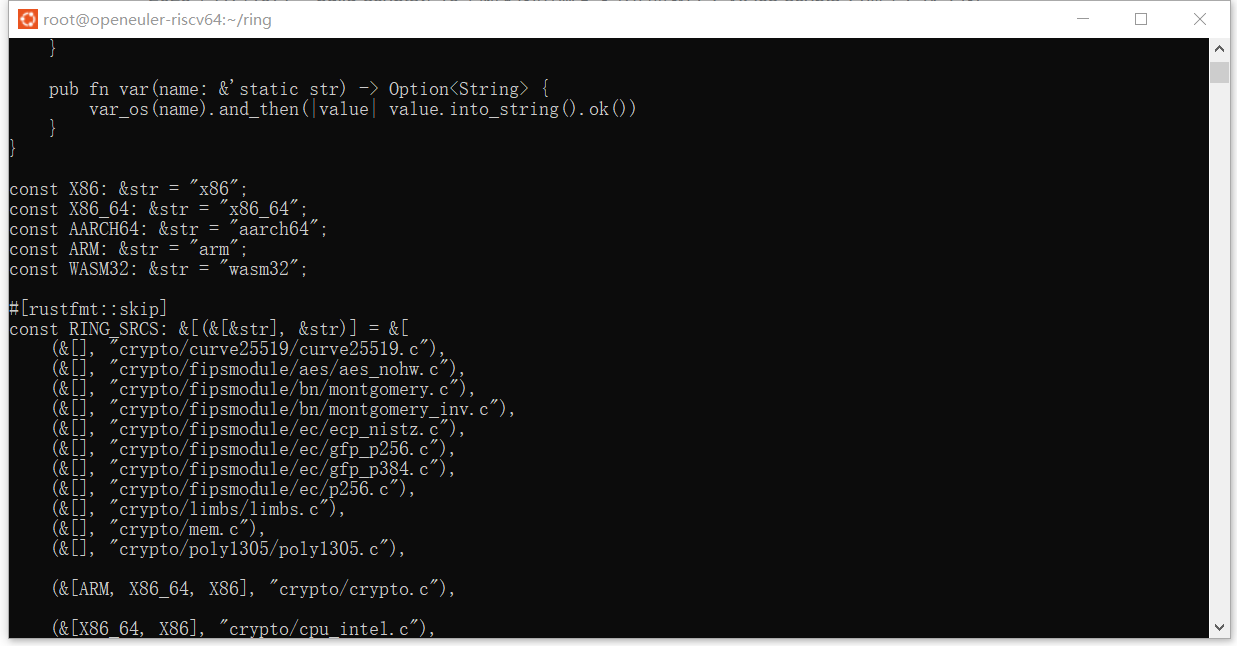
子集遍历
for (int i = 0; i < 1 << n; i ++ )
这个代码可以从 \(0\) 开始不重复的遍历每一个二进制数,因此时间复杂度 \(O(2^n)\)。
子集枚举
有的时候,我们希望枚举集合 \(i\) 所对应的所有自己,显然我们不可能循环套循环求与的方法做,时间复杂度是 \(O(2^{2n})\) 的,不优。
我们下面介绍子集枚举,他可以按照降序排序枚举集合。
for (int S = 0; S < 1 << n; i ++ )for (int T = S; T; T = (T - 1) & S)
\(T\) 最初恰好是集合 \(S\),在下一次循环时,我们让 \(T = (T - 1) \& S\),容易发现,把 \(T\) 的最后一个位掩码去掉了。
S = 1010100
T = 1010100 -> T = 1010011 & 1010100 = 1010000
再进行下一次循环,我们把刚才的比特恢复,消去下一个比特。
S = 1010100
T = 1010000 -> T = 1001111 & 1010100 = 1000100
接着再移去最后一个比特。
S = 1010100
T = 1000100 -> T = 1000011 & 1010100 = 1000000
以此类推,不难发现,T = (T - 1) & S 等价于我们倒序枚举连续集合的 T -- ,相当于无视了中间的 \(0\) 进行转移,这是优秀的,保证了每个子集唯一出现一次。
考虑每个枚举集合 \(S\) 的子集 \(T\) 的次数:
\[\begin{aligned}\sum_{S \subseteq \{1, \, 2, \, \cdots, \, n\}}\sum_{T \subseteq S}1 &= \sum_{i = 0}^n\binom{n}{i}2^i \\ &= (2 + 1)^n \\ &= 3^n\end{aligned}
\]
因此子集枚举的复杂度是 \(O(3^n)\)。
相关题目
这个东西通常用在一些 状压DP 的状态转移中,具体可以参考一下下面的题目。
最小斯坦纳树