导弹拦截问题-编程知识

导弹拦截问题

news/2025/4/2 1:30:52/文章来源:https://www.cnblogs.com/SIPnnnnn/p/18800738

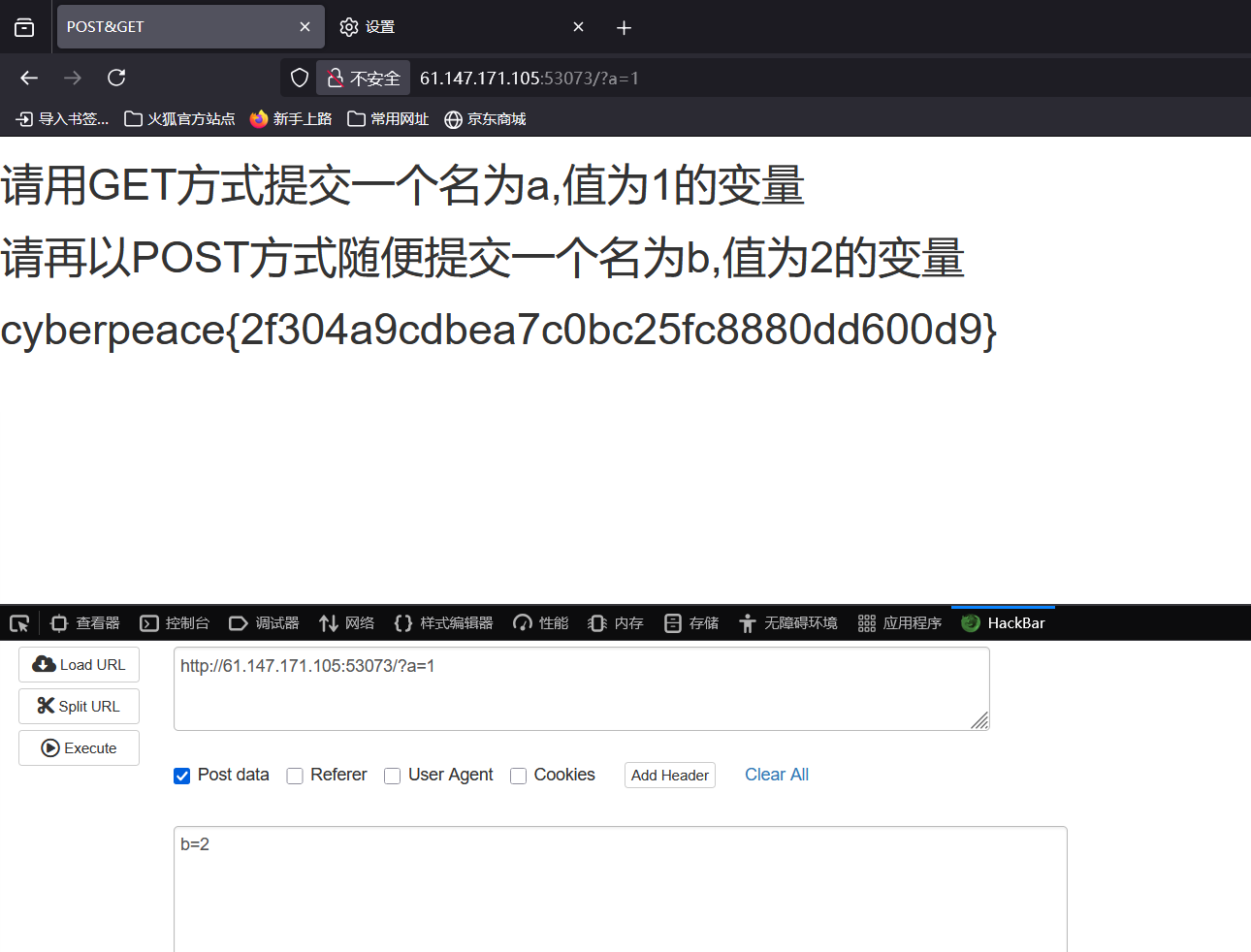
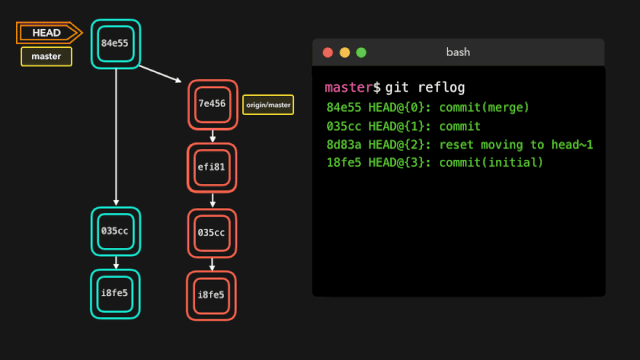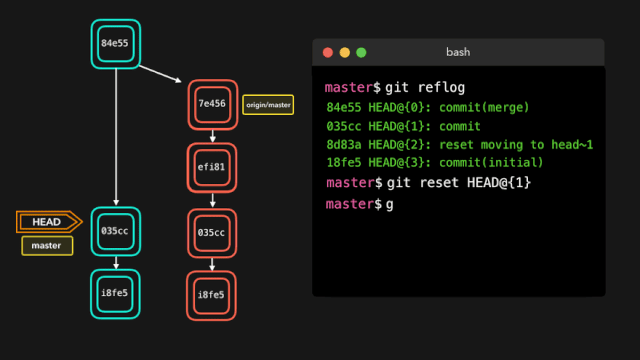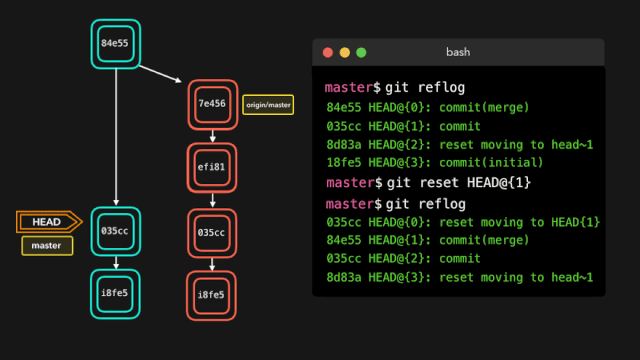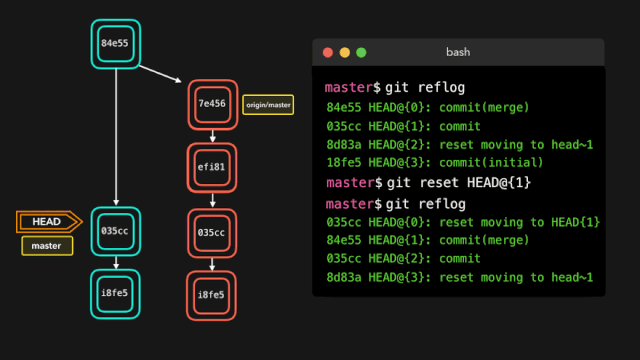
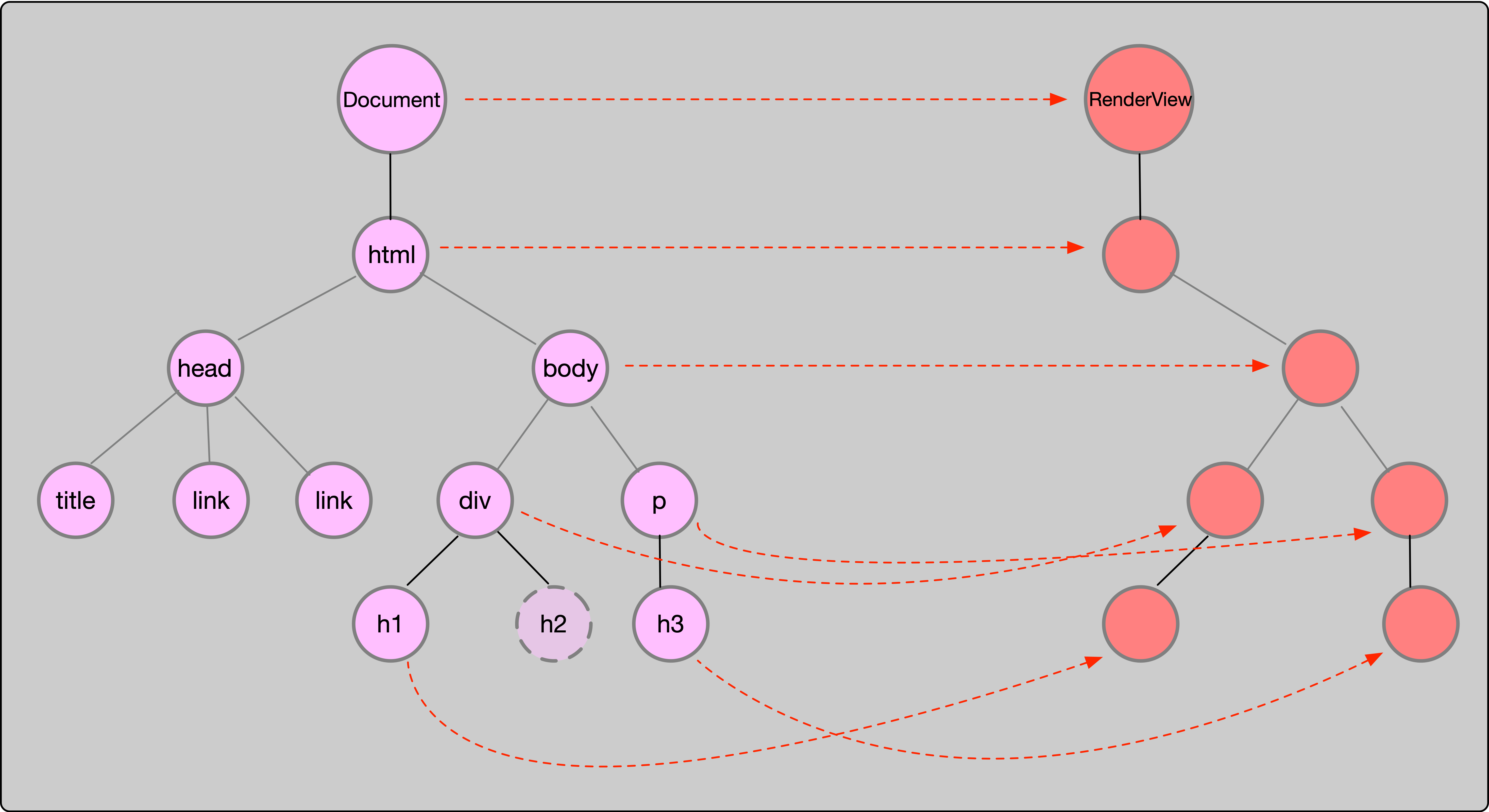
导弹拦截问题（也称为最长不上升子序列问题）是动态规划中的经典问题之一。问题的描述如下：
给定一个导弹飞行高度的序列，要求拦截所有导弹。拦截系统有一个限制：每次拦截的导弹高度不
能高于前一次拦截的导弹高度。问最少需要多少套拦截系统才能拦截所有导弹，或者一套拦截系统最多能拦截多少导弹。
这个问题可以转化为两个子问题：

1. 最少需要多少套拦截系统：即求导弹高度序列的最长上升子序列（LIS）的长度。
2. 一套拦截系统最多能拦截多少导弹：即求导弹高度序列的最长不上升子序列（LNIS）的长度。

示例数据：{189, 207, 155, 200, 99}

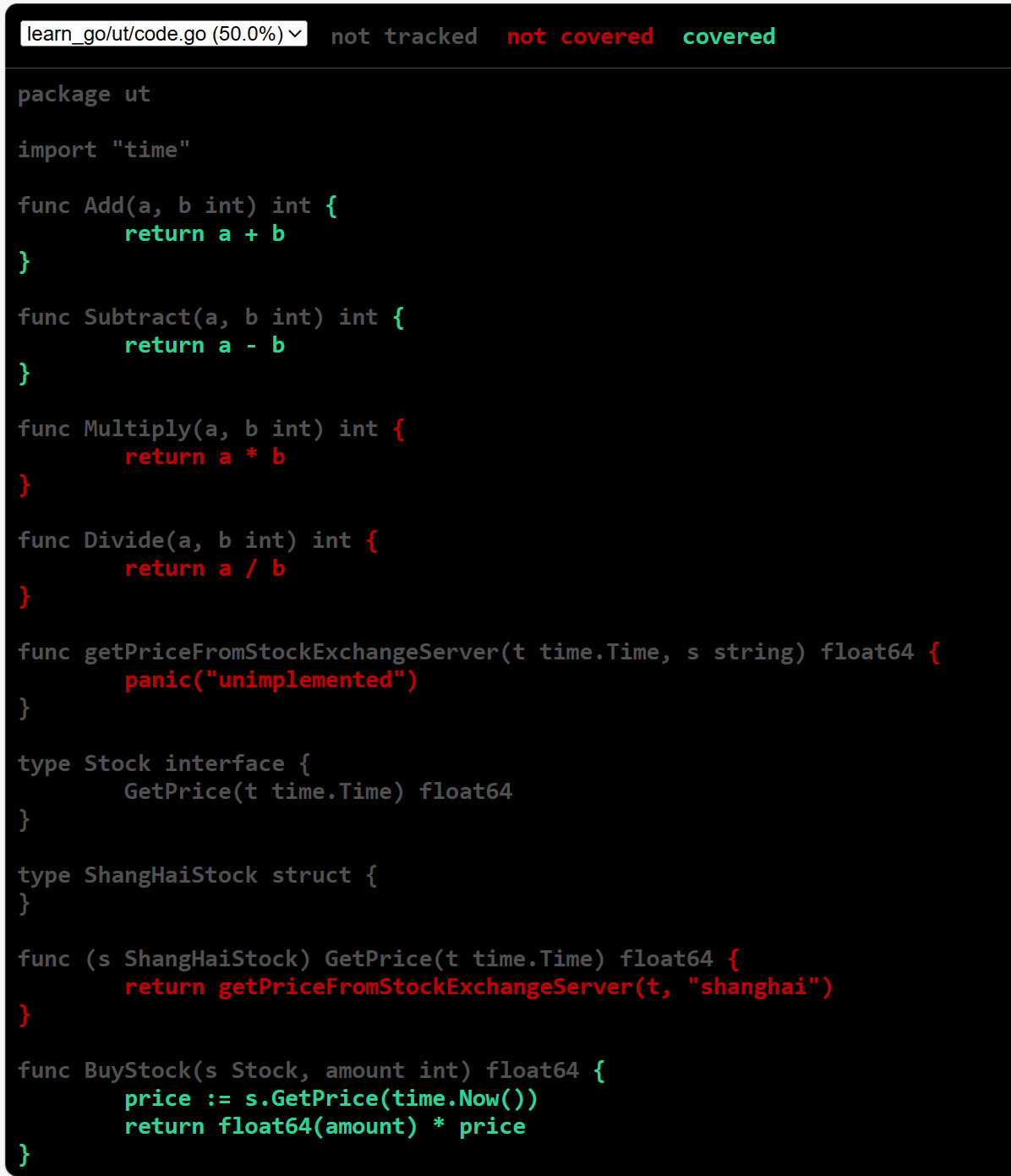
 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 
 4 int max_missiles(vector<int>&heights){
 5     int n=heights.size();
 6     vector<int>dp(n,1);//dp[i]=以height[i]结尾的最长不上升子序列
 7     for(int i=1;i<n;i++){
 8         for(int j=i;j<i;j++){
 9             if(heights[j]>=heights[i]){
10                 dp[i]=max(dp[j]+1,dp[i]);
11             }
12         }
13     }
14     return *max_element(dp.begin(),dp.end());
15 }
16 int max_w(vector<int>&heights){
17     int n=heights.size();
18     vector<int>dp(n,1);//dp[i]=以height[i]结尾的最长不上升子序列
19     for(int i=1;i<n;i++){
20         for(int j=i;j<i;j++){
21             if(heights[j]<heights[i]){
22                 dp[i]=max(dp[j]+1,dp[i]);
23             }
24         }
25     }
26     return *max_element(dp.begin(),dp.end());
27 }
28 int main(){
29     vector<int>heights={189,207,155,200,99};
30     int n=max_missiles(heights);
31     cout<<n<<endl<<max_w(heights);
32     return 0;
33 }