总体比例的方差

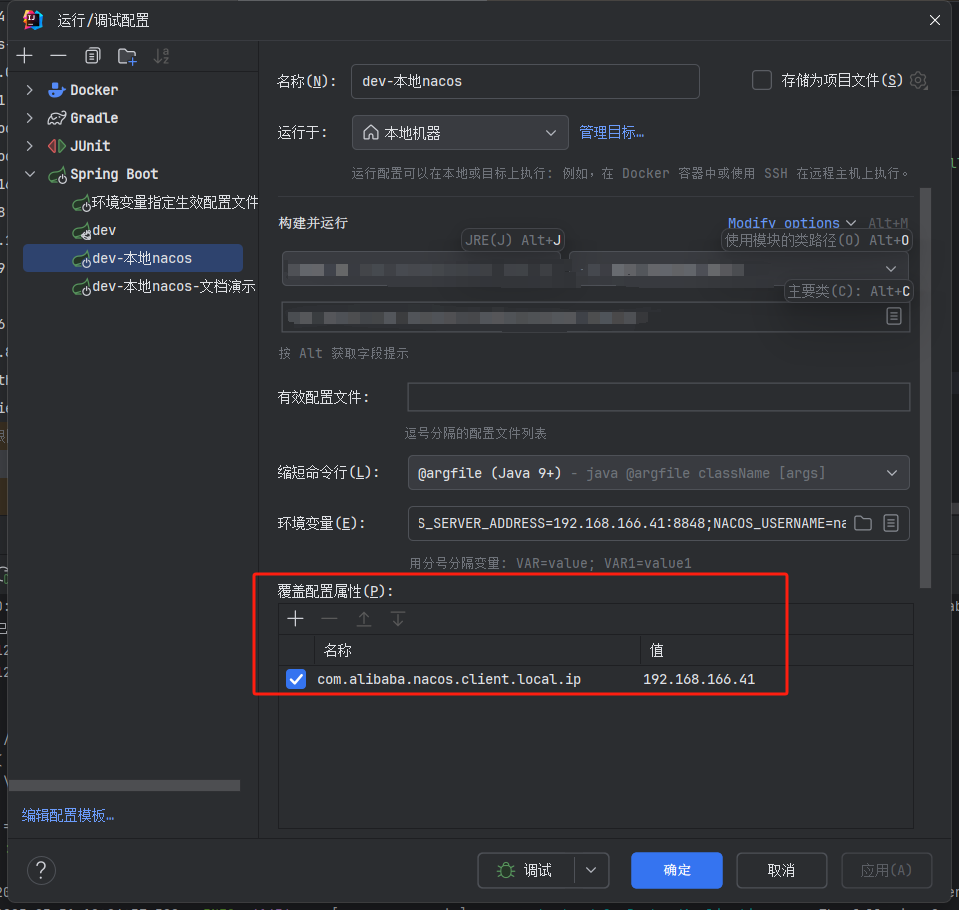
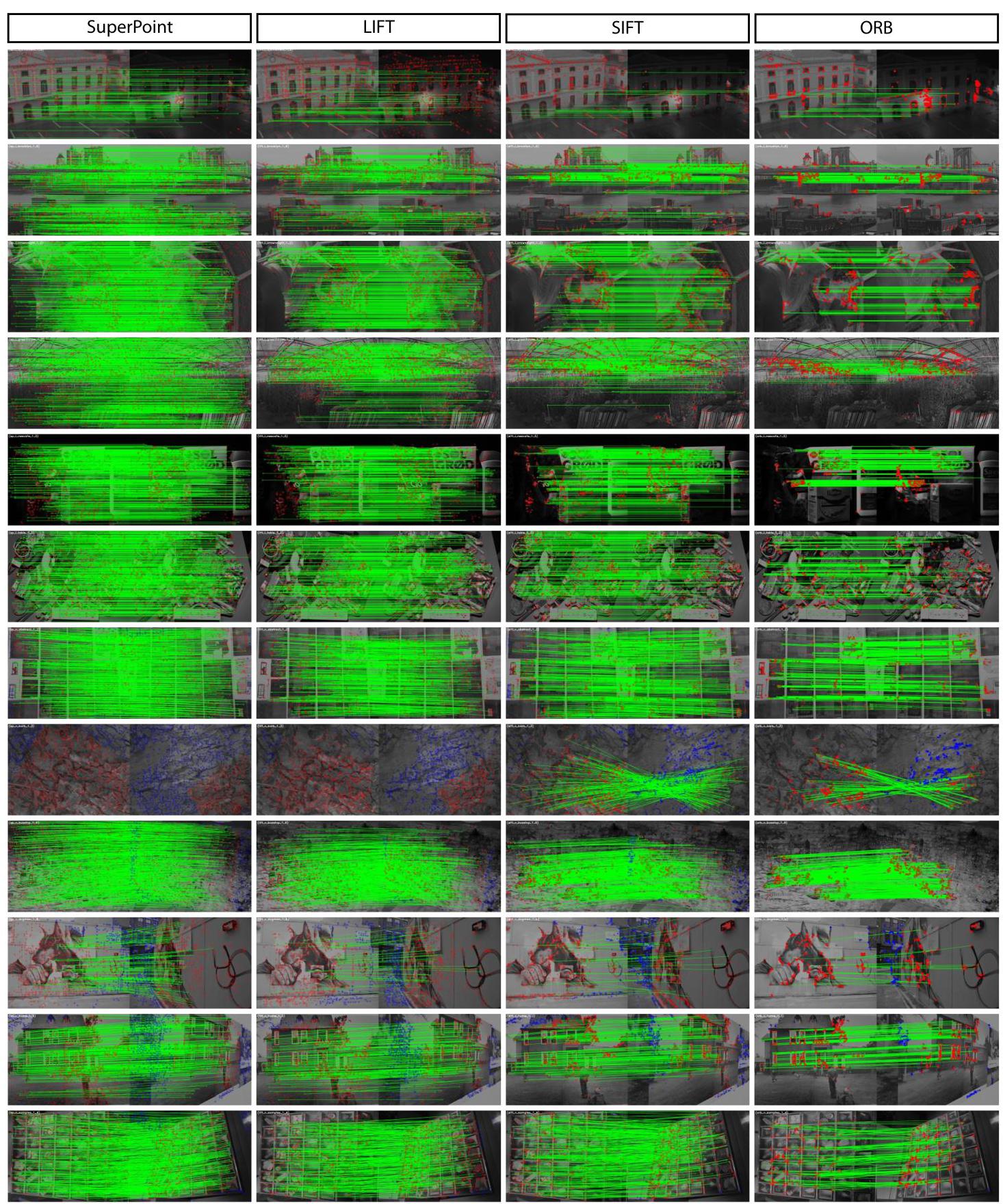
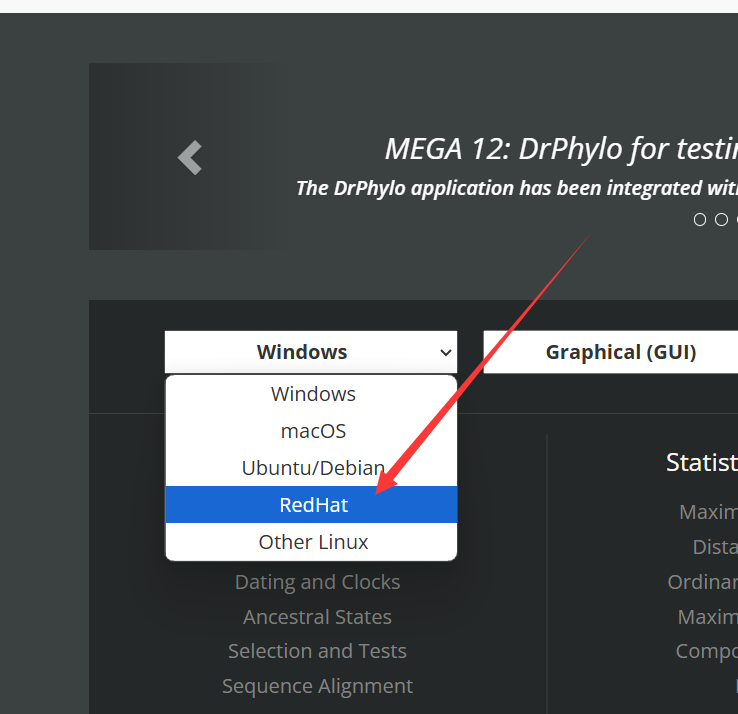
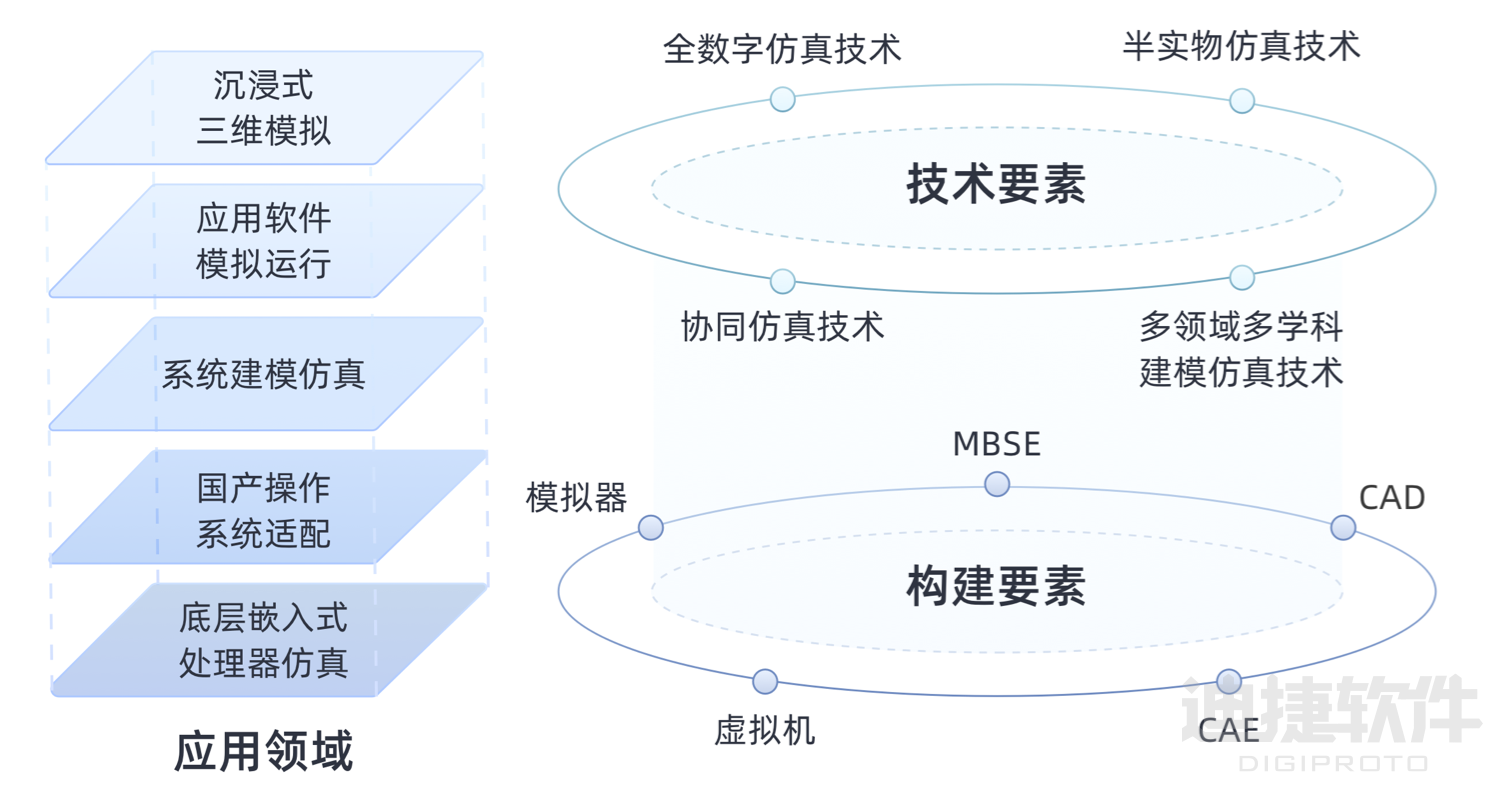
总体比例的方差推导（基于两点分布）

假设总体由 $ N $ 个个体组成，每个个体的某种特征可以取值 $ 1 $（成功）或 $ 0 $（失败）。我们用随机变量 $ X_i $ 表示第 $ i $ 个个体的取值，则 $ X_i $ 服从两点分布（Bernoulli 分布）：

\[X_i \sim \text{Bernoulli}(p), \quad P(X_i = 1) = p, \quad P(X_i = 0) = 1 - p \]

总体成功比例定义为：

\[P = \frac{1}{N} \sum_{i=1}^{N} X_i \]

我们要求 $ P $ 的方差，即：

\[\text{Var}(P) = \text{Var} \left( \frac{1}{N} \sum_{i=1}^{N} X_i \right) \]

1. 计算单个 $ X_i $ 的期望和方差

由于 $ X_i \sim \text{Bernoulli}(p) $，其期望和方差分别为：

\[E(X_i) = p \]

\[\text{Var}(X_i) = E(X_i^2) - [E(X_i)]^2 = p - p^2 = p(1 - p) \]

2. 计算总体比例的方差

由于 $ X_1, X_2, \dots, X_N $ 互相独立，我们利用方差的性质：

\[\text{Var} \left( \frac{1}{N} \sum_{i=1}^{N} X_i \right) = \frac{1}{N^2} \sum_{i=1}^{N} \text{Var}(X_i) \]

\[= \frac{1}{N^2} \times N p(1 - p) = \frac{p(1 - p)}{N} \]

3. 结论

因此，总体比例 $ P $ 的方差为：

\[\text{Var}(P) = \frac{p(1 - p)}{N} \]

这表明总体比例的方差随着总体规模 $ N $ 增大而减小，即当 $ N \to \infty $ 时，方差趋于 0，总体比例的波动性减少。