cf2090c
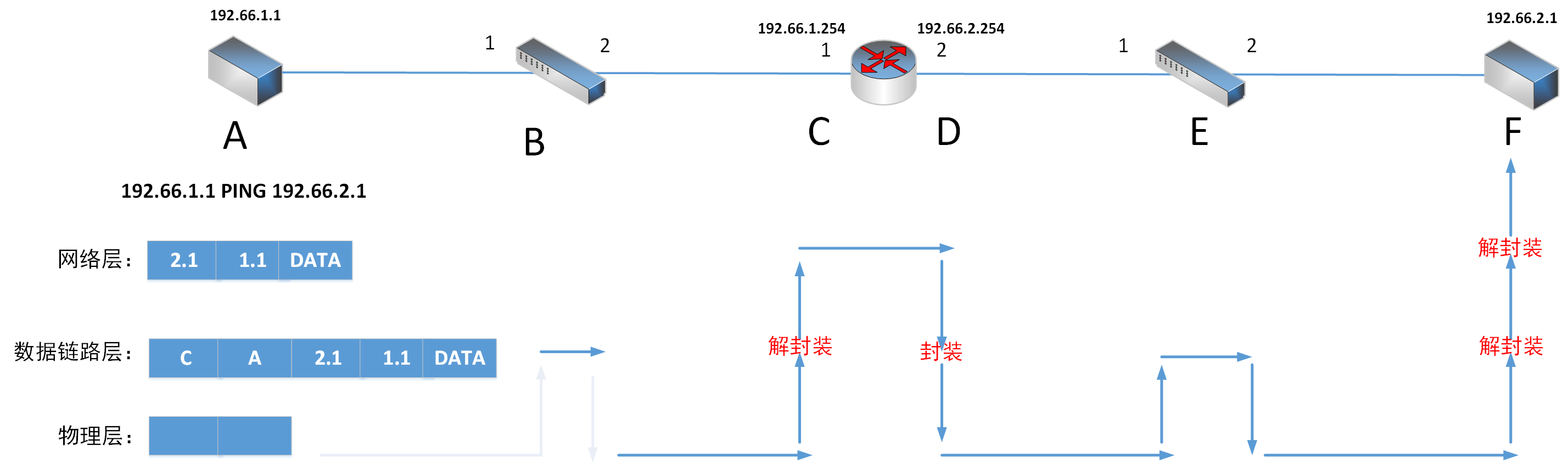
对于 \(t_i = 0\) 的人来说,选择空桌子是按照对角线斜向填充的,因为每次要选距离最小且 x 最小的空桌子。所以 y 方向上至少有一个人的桌子数量是 \(\sqrt{n}\) 级别的。
那么维护两个 set :一个维护空桌子,一个维护有人的桌子。预处理把可能的桌子的坐标和距离插到 set 里。查询时每次找符合条件的元素删除就行了。
cf1761e
分类讨论:
-
图已经连通:0 次。
-
图不连通:
-
如果有一个连通块大小为 1,那么直接对这个点操作就行了。
-
对于一个非完全的连通块,随便找一个点进行操作就行了,因为该点操作完和原本的连通块还是连通,同时与其他连通块联通了。
-
如果所有连通块都是完全的,那么至少需要两次操作。因为可以先选择一个连通块的一个点操作,这样这个点就和剩下的所有连通块连通了。然后再选一个连通块的一个点操作,这样这个点就和包括第一个连通块的其他连通块都连通了,同时当前这个连通块剩下的点已经和第一个连通块连通了,所以整个图就连通了。但是当只有两个连通块的时候不能这么做,只能从其中一个连通块上一个一个把点拆下来连到另一个连通块上,这样的最小操作次数就是两个连通块大小的 min。
-
总结一下:dfs 求连通块数量,同时找是否有大小为 1 的连通块,是否有不是完全图的连通块。然后根据上面的分类就行了。
但是写完发现 wa 了,为什么呢?因为在讨论中忽略了一个重要的点:对一个连通块选择点操作的时候,有可能把原本的连通块变得 不连通 了!!!!
所以选点的时候不能选 割点。更进一步,我们只需要选择一个度数最小的点就行了,因为如果这个度数最小的点是割点,度数为 \(d\),那么与其相连的所有点的度数至少为 \(d\),也就是说这个图是一个完全图,没有割点,矛盾了。
gym103438
G
注意到 \(w_{ij}\) 是对称的,也就是说与 \(a_i\),\(b_i\) 的顺序是无关的。更进一步的说,令 \(a_i < b_i\),那么 \(w_{ij} = \max\{b_i - a_j, b_j - a_i\}\)。假设 \(b_i - a_j < b_j - a_i\),移项有 \(a_i + b_i < a_j + b_j\)。所以按照 \(a_i + b_i\) 从大到小排序,然后取前 \(n\) 个的 \(b_i\) 减去 后 n 个的 \(a_i\) 就是答案。
J
假设 A,B,C 的数量为 c1,c2,c3。那么当 c1 + c2 < c3 或 c1 + c3 < c2 或 c2 + c3 < c1 时是无解的,因为没有足够多的对应字母进行匹配。更进一步,我们可以得到 AB,BC,AC的匹配次数 \(\frac{c_1 + c_2 - c_3}{2}\),\(\frac{c_2 + c_3 - c_1}{2}\),\(\frac{c_1 + c_3 - c_2}{2}\)。
然后,AB,AC,BC 的匹配本质上是括号匹配,A 是左括号,C 是右括号,B 既可以是左括号也可以是右括号。那么不妨从 B 入手。
为了尽可能满足匹配数量,让前 \(BC = \frac{c_2 + c_3 - c_1}{2}\) 个 B 用来匹配 BC,剩下的后 \(\frac{c_1 + c_2 - c_3}{2}\) 个 B 用来匹配 AB,这样能尽量的匹配更多的 BC 和 AB。
剩下没有匹配的 A 和 C 就两两匹配。当匹配过程中找不到右括号或左括号的时候无解,达不到对应匹配次数时无解。
cf1665d
有意思的交互提。
首先有 \(\gcd(x + a, x + b) = \gcd(x + a, |b - a|)\)。询问次数是 \(\log{x}\) 级别的,提示我们从二进制的角度思考问题。
那么如何从二进制角度逐步确定 x 呢?首先从低位往高位猜,消除高位对低位的影响,假设现在猜到了第 \(i\) 位,已经知道了前 \(i - 1\) 位的答案为 \(x'\),那么构造出 \(a = 2^{i - 1} - x\),\(b = 2^{i - 1} + 2^{i} - x\),这样相当于询问了 \(\gcd(x, 2^{i})\),如果第 \(i\) 为 1,那么询问结果是 \(2^{i}\)。否则第 \(i\) 位为 0。
gym104008e
三角形的面积可以通过叉积表示,现在已知 \(\overrightarrow{AB} = (u, v)\),设 \(\overrightarrow{AC} = (p, q)\),那么面积 \(2S = |uq - pv|\)。
由裴蜀定理可知,对于方程 \(ax + by = n\),有正整数解的充要条件是 \(\gcd(a, b) \mid n\)。所以面积取到最小的时候,p,q 应该满足方程 \(uq - pv = \gcd(u, v)\)。用 exgcd 解出一个解就能得到 C 的坐标了。
CSP 认证 T4
简要题意:给定长度为 \(n\) 的数组 \(a\),定义一个区间 \([l, r]\) 的价值为 \(l \times r \times \gcd(a_l, a_{l+1}, \cdots, a_r)\)。求所有区间的价值之和。\(n \leq 10^6\),\(a_i \leq 10^9\)。
不保证以下文字的正确性。
首先固定 \(l\),考虑怎么算以其为左端点的价值之和。