Verilog典型电路设计之log函数的Verilog HDL设计
log函数是一种典型的单目计算函数,与其相应的还有指数函数、三角函数等。对于单目计算函数的硬件加速器设计一般两种简单方法:一种是查找表的方式;一种是使用泰勒级数展开成多项式进行近似计算。这两种方式在设计方法和精确度方面有很大的不同。查找表方式是通过存储器进行设计,设计方法简单,其精度需要通过提高存储器深度实现,在集成电路中占用面积大,因此着这种方式通常在精度要求不高的近似计算中使用。泰勒级数展开方式采用乘法器和加法器实现,可以通过增加展开级数提高计算精确度。例:用Verilog HDL设计采用查找表方式的log函数,输入信号位宽4bits,输出信号位宽8bits
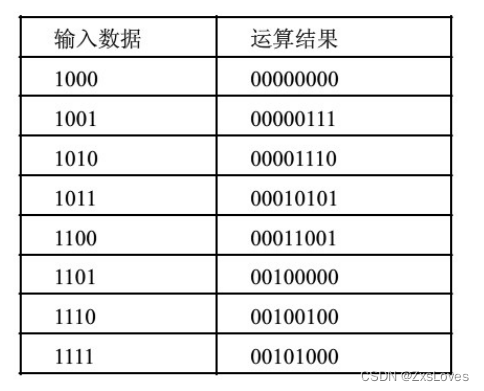
其中输入数据为一位整数位三位小数位精确到2-3,输出结果两位整数位六位小数位精确到26。其Verilog HDL程序代码是:
module log_lookup(x,clk,out);
input [3:0] x;
input clk;
output [7:0] out;
reg[7:0] out;
always@(posedge clk) begin
case(x)
4'b1000:out<=8'b00000000;
4'b1001:out<=8'b00000111;
4'b1010:out<=8'b00001110;
4'b1011:out<=8'b00010101;
4'b1100:out<=8'b00011001;
4'b1101:out<=8'b00100000;
4'b1110:out<=8'b00100100;
4'b1111:out<=8'b00101000;
default:out<=8'bz;
endcase
end
endmodule
下面是testbench
module log_lookup_tb;
reg clk;
reg [3:0]x;
wire [7:0] out;
initial begin
x=4'b1000;
clk=1'b0;
repeat(7)
#10 x=x+1;
end
always
#5 clk=~clk;
log_lookup U1(.x(x),.clk(clk),.out(out));
endmodule
例:用Verilog HDL设计采用泰勒级数展开方式的log函数,输入信号位宽4bits,输出信号位宽8bits
泰勒级数的定义:若函数f (x)在点的某一邻域内具有直到(n+1)阶导数,则在该邻域内f (x)的n阶泰勒公式为:
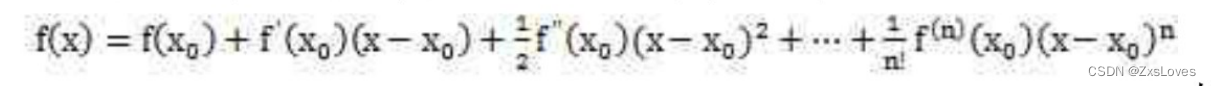
泰勒级数可以将一些复杂的函数用多项式相加的形式进行近似,从而简化其硬件的实现。
logax在x=b处的泰勒展开为
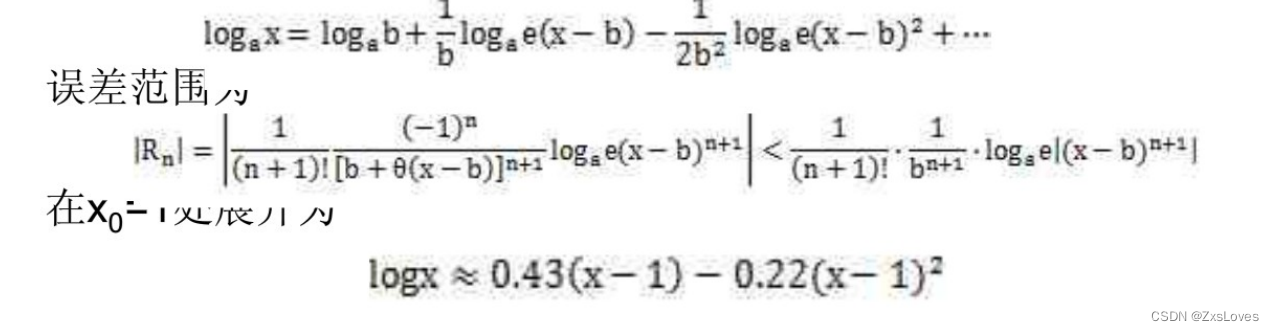
误差范围为:
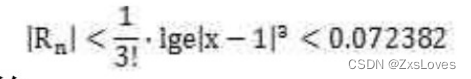
电路结构图如图所示
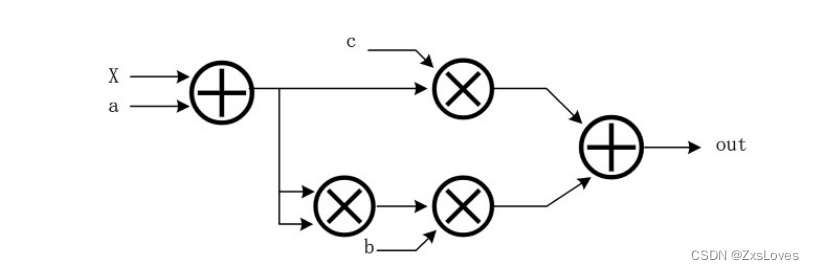
上述的log函数在X=1处展开,并且要求X的取值范围为1<X<2,输入4位二进制数据X精确到2-3,其中一位整数位四位小数位,输出8位二进制数据精确到2-6,其中两位整数位六位小数位。设计当中所用到的乘法器和减法器均采用前文所给出的减法器和乘法器。
module log(x,out);
input[3:0] x;
output[7:0] out;
wire [3:0] out1;
wire [7:0] out2,out3, out5, out;
wire [3:0] out4;
assign out4={out3[7:4]};
assign out1=x-4'b1000;//(x-1)
wallace U1(.×(out1),.y(4'b0111),.out(out2));
wallace U2(.x(out1),.y(out1),.out(out3));
wallace u3(.x(out4),.y(4'b0011),.out(out5));
assign out=out2-out5;
endmodule
下面是所显示的testbench
module log_tb;
reg [3:0] x=4'b1000;
wire [7:0] out;
log U1(.x(x),.out(out));
always
#10x=x+1;
always@(x)begin
if(x==4'b0000)$stop;
end
endmodule