数据结构做题记录-编程知识

数据结构做题记录

news/2025/4/3 0:31:31/文章来源:https://www.cnblogs.com/liuir/p/18804461

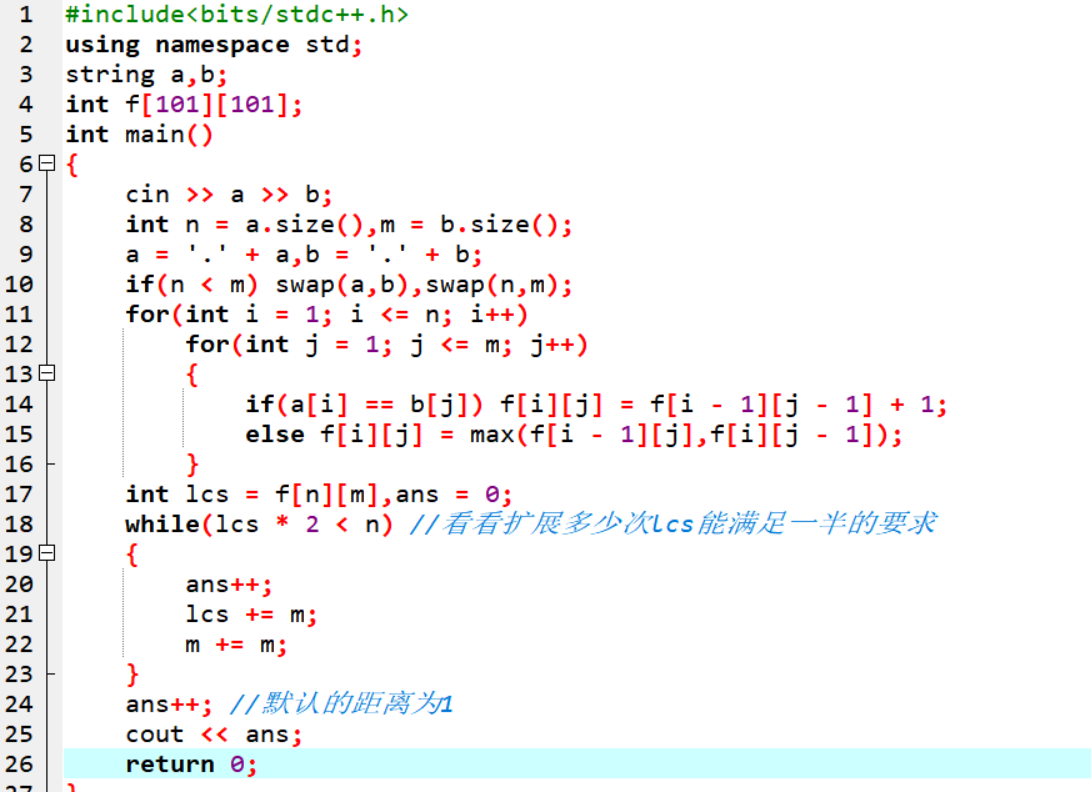
\(\text{I}\). luoguP5142 区间方差

容易得到

\[d=\dfrac{n\sum_{i=1}^na_i^2-\left(\sum_{i=1}^na_i\right)^2}{n^2} \]

线段树维护出 \(\sum a_i\) 和 \(\sum a_i^2\) 即可。

\(\text{II}\). CF739C Alyona and towers

考虑现将原数组差分，则可以将题目转换为求一个区间满足先是一串正数，再是一串负数。

而这个可以用类似最大子段和的方法维护，即对于每个区间维护最大长度，从左边开始的最大长度和从右边开始的最大长度。

\(\text{III}\). [JSOI2018] 列队

将一些数变成连续的数可能不太好处理。于是按套路减去它的排名，然后变成相同的数。

具体地，有

\[ans=\sum_{i=l}^r\left|a_i-rk_i-k+1\right| \]

其中 \(rk_i\) 表示 \(a_i\) 在 \(a_{[l,r]}\) 内的排名。

为方便先将 k--。

按 \(a_i\) 从小到大考虑每个 \(i\)，因为 \(a_i\) 互不相同，所以 \(a_i\) 的增长一定不会慢于 \(rk_i\) 的增长。于是满足 \(a_i-rk_i-k\ge0\) 的一定是一段后缀。

考虑在主席树上二分出分界点，然后就可以 \(O(1)\) 计算了。

时间复杂度 \(O(n\log n)\)。

\(\text{IV}\). luoguP3730 曼哈顿交易

直接暴力莫队可以用平衡树求出第 \(k\) 小，时间复杂度为 \(O(n\sqrt n\log n)\)。但毒瘤出题人显然不想要它通过。

由于不可差分，不能二次离线，只能考虑用 \(O(1)-O(\sqrt n)\) 的分块。

对值域分块，维护出每个值的出现次数和每个块内所有值的总出现次数。查询时先跳整块，再跳散块即可。

时间复杂度 \(O(n\sqrt n)\)。

\(\text{V}\). *luoguP7708 八云蓝自动机 Ⅰ

带修莫队可以做到 \(O(n^\frac{5}{3})\)，很可惜不能通过。

首先单点修改可以新建一个新点变成交换操作。

考虑在莫队时维护以下信息：

现序列的状态 \(a\)。
现位置 \(i\) 上的数的原位置 \(rev_i\)。
原位置 \(i\) 上的数的现位置 \(pos_i\)。
现序列上位置 \(i\) 被询问的次数 \(add_i\)。

当右端点右移 \(r-1\to r\) 时：

若 \(r\) 是交换 \(x,y\)，直接交换 \(a_x,a_y\)，\(rev_x,rev_y\)，\(pos_{rev_x},pos_{rev_y}\)，\(add_x,add_y\)。
若 \(r\) 是询问 \(x\)，令 \(ans\leftarrow ans+a_x\)，\(add_x\leftarrow add_x+1\)。

当左端点左移 \(l+1\to l\) 时：

若 \(l\) 是交换 \(x,y\)，直接交换 \(a_{pos_x},a_{pos,y}\)，\(rev_{pos_x},rev_{pos_y}\)，\(pos_x,pos_y\)。然后答案加上交换后的 \((a_{pos_x}-a_{pos_y})(add_{pos_x}-add_{pos_y})\)。
若 \(l\) 是询问 \(x\)，令 \(ans\leftarrow ans+a_{pos_x}\)，\(add_{pos_x}\leftarrow add_{pow_x}+1\)。

剩余两种情况是类似的，只不过符号不同。

时间复杂度 \(O(n\sqrt n)\)。

\(\text{VI}\). *[APIO2019] 路灯

点亮路灯相当于连接 \((i,i+1)\)，熄灭路灯相当于断开 \((i,i+1)\)。

考虑维护出每个点所属的连通块，以及该连通块的左右端点。那么每次修改相当于区间赋值，可以用 ODT 实现。

记 \(bel_i\) 表示 \(i\) 所在的连通块，\(l_i,r_i\) 为第 \(i\) 个连通块的左右端点。那么点亮路灯就会使 \([l_{bel_i},i]\) 与 \([i+1,r_{bel_{i+1}}]\) 联通。

使用提前计算贡献的方法。点亮是给 \([l_{bel_i},i]\) 到 \([i+1,r_{bel_{i+1}}]\) 的贡献加上 \(q-T\)（\(T\) 为当前时间），熄灭时就减去。注意到这是一个动态矩形加，单点查的操作，可以用 cdq 分治+扫描线或树套树解决。

\(\text{VII}\). [POI2011] MET-Meteors

先考虑对每个国家怎么做。

可以想到二分，判断是可以将前 \(mid\) 个询问的操作都加上贡献。

但这样太浪费了，于是可以整体二分再用树状数组维护。

\(\text{VIII}\). [Ynoi2006] rldcot

由于 \(\operatorname{lca}\) 总共就只有 \(n\) 个，所以肯定可以找支配对。

套路的树上启发式合并，每次加入一个点时找到它的前驱和后继，这样肯定支配了其他点。因为每个点只会加入 \(O(\log n)\) 次。所以这样有 \(O(n\log n)\) 个支配对。

若把一组询问看作一个点 \((l,r)\)，那么每个支配对的贡献就是矩形操作。考虑把 \(dep(\operatorname{lca}(i,j))\) 相同的支配对放到一起，那么就要求一些 2-side 矩形的并。

这可以经典的转化为 4-side 矩形加问题，然后用扫描线+树状数组解决。

时间复杂度 \(O(n\log^2+q\log n)\)。

\(\text{IX}\). Luogu P7811 [JRKSJ R2] 你的名字

考虑根号分治：

若 \(k\le B\)，直接暴力求出 \(a_i\bmod k\) 的值后做 RMQ。离线逐块处理可以做到线性空间，而时间是 \(O(nB+q\log n)\) 的。
若 \(k>B\)，则枚举每一个 \(ik\)，那么答案就是所有 \(ik\) 的后继模上 \(k\) 的值中最小的那个。用主席树可以做到 \(O(\frac{qV}{B}\log n)\)，但不能通过。

考虑将问题规约到求区间 \([l,r]\) 内 \(x\) 的后继。

考虑按 \(x\) 从大到小扫描，则问题变为带修 RMQ。注意到修改只有 \(O(n)\) 次，而查询有 \(O(\frac{qV}{B})\) 次，于是直接上底层分块的猫树即可。

具体的，先将序列分块后再建猫树。每次修改时就重构所在块的信息并且重构猫树，查询是就直接在猫树上查。这样就可以做到 \(O(\sqrt n)-O(1)\) 的带修 RMQ。

时间复杂度 \(O(n\sqrt n+\frac{qV}{B})\)。