一、概述
CherryStudio 是一款集多模型对话、知识库管理、AI 绘画、翻译等功能于一体的全能 AI 助手平台。 CherryStudio 高度自定义的设计、强大的扩展能力和友好的用户体验,使其成为专业用户和 AI 爱好者的理想选择。无论是零基础用户还是开发者,都能在 CherryStudio 中找到适合自己的AI功能,提升工作效率和创造力。
官方地址:https://cherry-ai.com/
二、安装
访问官方地址,下载客户端,根据提示,安装即可。
三、使用
在上一篇文档中,本地已经部署好了Ollama,并成功运行了qwen2.5,链接地址:https://www.cnblogs.com/xiao987334176/p/18804232
接下来,使用AI客户端,来调用Ollama运行的模型。这个客户端,我认为是最好的AI客户端,支持市面上所有的AI大模型。
打开客户端,点击左下角的设置

点击模型服务-->Ollama
输入API密钥,API地址,点击添加
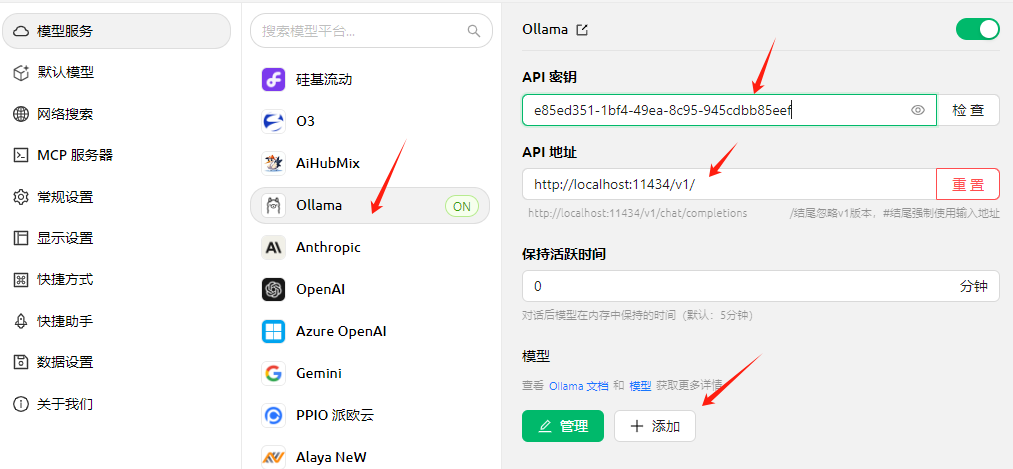
输入qwen2.5:3b,点击添加模型。
注意:这里输入的值,就是ollama run后面的值。

添加成功后,这里会展示出来
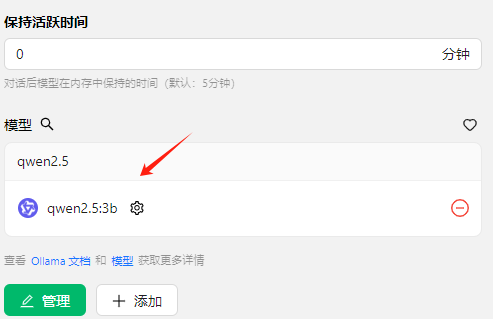
手动选择模型,qwen2.5:3b
然后提问,就会有回答
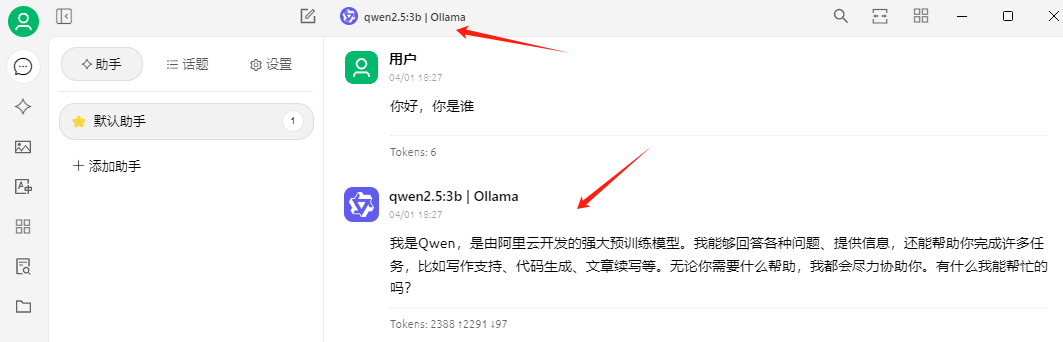
后续ollama运行了其他模型,也可以添加过来,进行本地测试,非常方便。