一、选择填空判断题

题型一（顺序、二分查找的概念）

1、顺序查找适用于存储结构为（）的线性表。
A、顺序存储结构或者链式存储结构
B、散列存储结构
C、索引存储结构
D、压缩存储结构

解析：（A）
顺序查找属于线性查找，从线性表的一端开始，依次检查所给定的关键字是否满足条件，若找到符合条件的元素，则查找成功；否则，查找失败。

由于线性表有顺序存储和链式存储两种存储方式，顺序查找对这两种存储方式都适用，若对于顺序表，则通过数组的下标依次查找；对于链表，则通过指针依次查找，在链表中只能进行顺序查找。

2、使用二分查找方法时，对线性表的存储结构及特性的要求是（）。
A、元素的链表
B、有序的链表
C、无序的顺序表
D、有序的顺序表

解析：（D）
二分查找（折半查找）属于线性查找，每次取中间元素进行比较，一直缩小范围继续进行查找，直到查找到相关元素为止，找到即查找成功；否则，查找失败。

二分查找只适用于有序的顺序表，它要求线性表具有随机存取，前提是查找表中必须是按关键字大小有序排列。

3、在一个顺序存储的有序线性表上查找一个数据时，既可以采用折半查找，也可以采用顺序查找，但前者比后者的查找速度（）。
A、必然快
B、取决于表是递增还是递减
C、在大部分情况下要块
D、必然不快

解析：（C）
顺序查找的优点是对元素的存储没有要求，可以顺序存储和链式存储，且对表内的有序性也没有要求，但其缺点是当n较大时，ASL较大，导致效率低。在平均情况下，折半查找比顺序查找的效率高。

题型二（分块查找的概念）

1、（填空）长度为7225的有序表，采用分块查找进行查找，为了提高顺序查找索引表和顺序查找相应块的效率，则应将有序表分成_________块，每块长度为_________，此时平均查找长度是_________。

解析：85、85、86
分块查找的平均查找长度等于索引查找和块内查找的平均查找长度之和，即ASL=ASL_索引表+ASL_子表。若查找表长度为n，被均匀地分为b块，且每块有s个记录，则在等概率的情况下，若对块内和索引表内都采用顺序查找的平均查找长度为：ASL=ASL_索引表+ASL_子表=(b+1)/2+(s+1)/2=(s2+2s+n)/2s，且每块有记录为s= √n。

所以被分为85块，每块的最佳长度应该为√7225=85最合适，为每个块建立索引，索引表中索引项的个数为85，即每块长度为85，从85个块中进行顺序查找，即(b+1)/2=(85+1)/2=43；在每个块中进行顺序查找，即(s+1)/2=(85+1)/2=43，故平均查找长度为43+43=86。

题型三（关键字比较次数）

1、已知有序表（13，18，24，35，47，50，62，83，90，115，134），当二分查找值为90的元素时，查找成功的比较次数为（）。
A、1
B、2
C、4
D、6

解析：（B）
low指针一开始指向13，high指针一开始指向134，所以mid指向50，第一次比较90>15，所以low+1，high指针不变，此时low指针指向62，high指针指向134，即mid指向90，即第二次比较时找到目标元素，查找成功的比较次数为2。

2、已知一个长度为16的顺序表L，其元素按关键字有序排列，若采用折半查找法查找一个L中不存在的元素，则关键字的比较次数最多为（）。
A、4
B、5
C、6
D、7

解析：（B）
对于顺序查找，查找成功或不成功，关键字的比较次数始终是n+1次，当定位至第i个元素时，关键字的比较次数为n-i+1。（默认代码中采用监视哨，若不采用监视哨，关键字的比较次数为n）

对于折半查找，查找成功和查找失败的最多比较次数相同，均为⌈log2(n+1)⌉，由于折半判定树不是一棵满二叉树，其各分支高度相差为0或1，且由于最多相差为1，所以查找失败的最少次数为⌈log2(n+1)⌉-1。故题中关键字的比较次数最多为⌈log2(n+1)⌉=⌈log2(16+1)⌉=⌈log2(17)⌉= 4.087…，取大于等于该值的最小整数（向上取整），即5。

3、为提高查找效率，对有65025个元素的有序顺序表建立索引顺序结构，在最好情况下查找列表中已有元素最多需要执行（）次关键字比较。
A、10
B、14
C、16
D、21

解析：（C）
每个索引块的大小为 √65025=255，为每个块建立索引，索引表中索引项的个数为255，当对索引表和块内都采用折半查找时，查找效率最高，即ASL=ASL_索引表+ASL_子表=⌈log2(b+1)⌉+⌈log2(b+1)⌉=2⌈log2(b+1)⌉=2×8=16。

二、应用题

题型一（二分查找判定树）

1、若一个有序顺序表表长为12：
（1）画出对其进行二分查找的二分查找判定树；
（2）在等概率假定条件下，计算对该表进行二分查找时查找成功和查找失败的平均查找长度。

解析：（1）二分查找判定树的求法：
①确定根结点：取low=1，high=12，mid向下取整（小于等于这个数的最大整数），即mid=⌊(low+high)/2 ⌋=⌊6.5⌋=6，即元素6为判定树的根结点，如下：


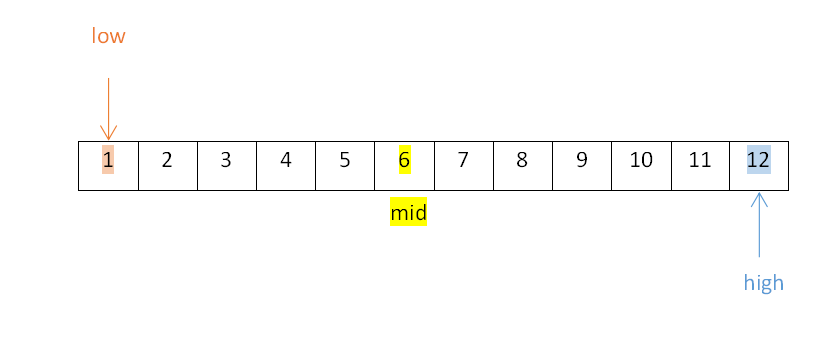
②从mid的左右子表开始进行查找。
③mid左子表查找：

• 【左子树】此时low=1不变，high变为mid-1，mid=6，即high=mid-1=6-1=5，改变后的mid=⌊(low+high)/2⌋=⌊6/2⌋=⌊3⌋=3，所以根结点6的左子树为3，如下：
  
  
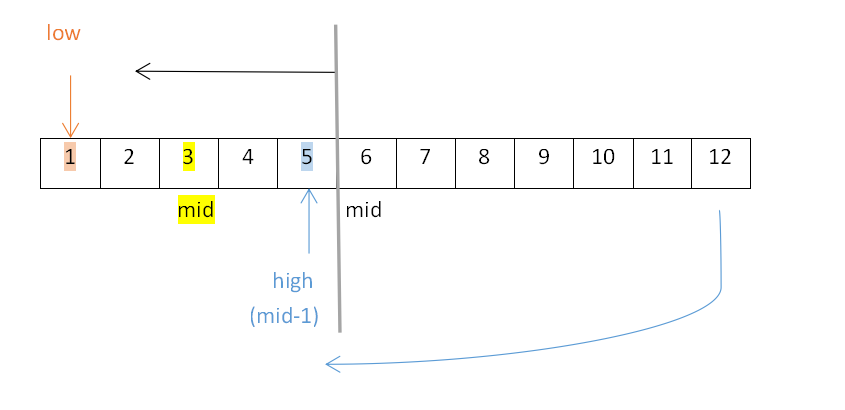
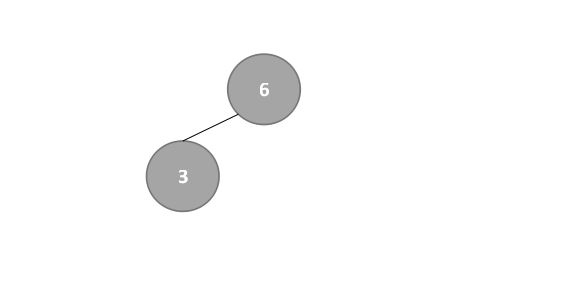
• 继续探索左子树，low=1不变，high变为mid-1，mid=3，即high=mid-1=3-1=2，改变后的mid=⌊(low+high)/2 ⌋=⌊3/2⌋=⌊1.5⌋=1，所以结点3的左子树为1，如下：
  
  
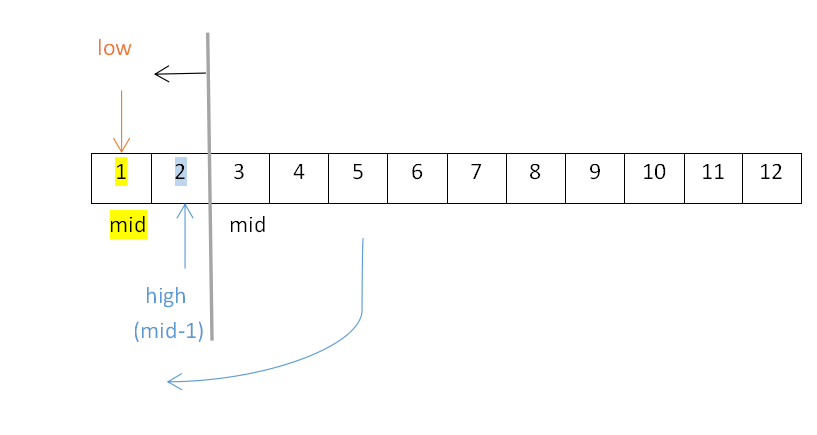
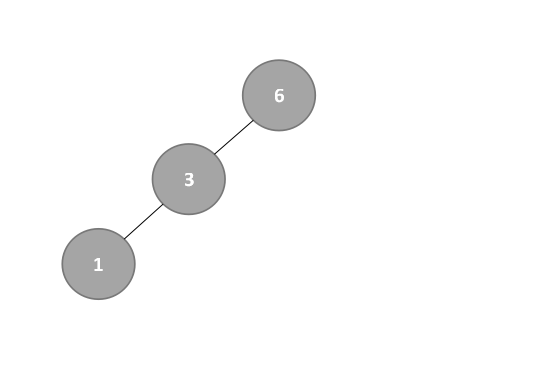
• 若继续探索左子树，易知结点1无左子树。
• 从结点1开始探索右子树，high=2不变，low为mid+1，mid=1，即low=mid+1=1+1=2，改变后的mid=⌊(low+high)/2 ⌋=⌊4/2⌋=⌊2⌋=2，所以结点1的右子树为2，如下：
  
  
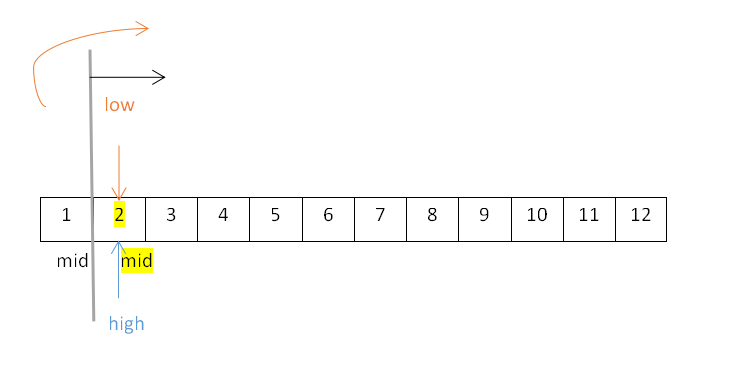
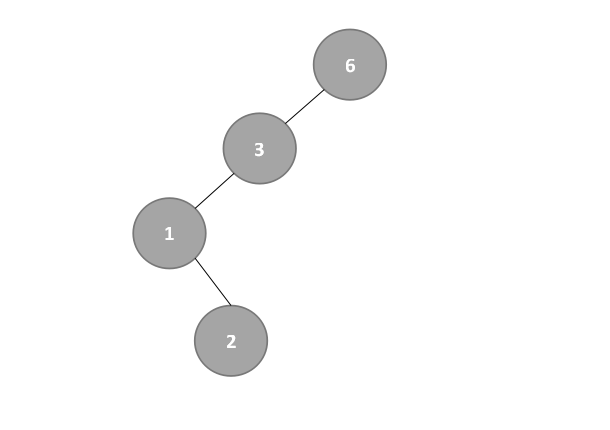
• 【右子树】此时从结点3开始探索右子树，high=5不变，low为mid+1，mid=3，即low=mid+1=3+1=4，改变后的mid=⌊(low+high)/2 ⌋=⌊9/2⌋=⌊4.5⌋=4，所以结点3的右子树为4，如下：
  
  
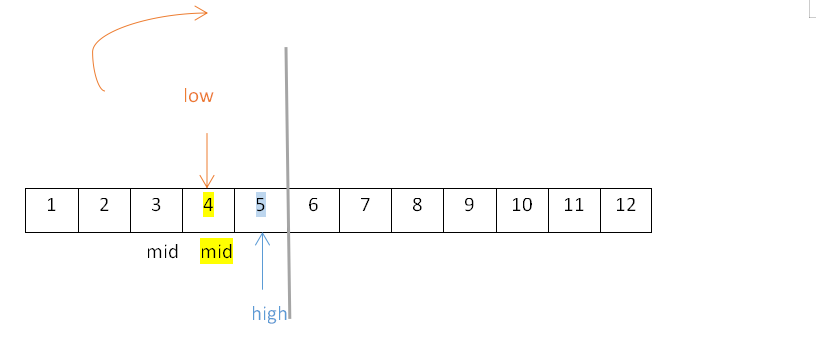
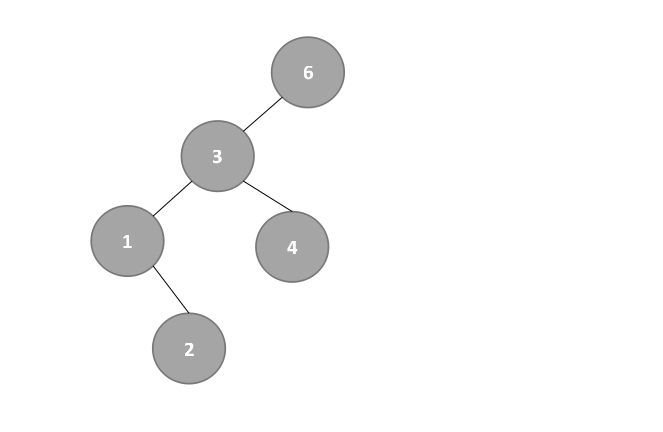
• 若继续探索左子树，易知结点4无左子树。
• 此时从结点4开始探索右子树，high=5不变，low为mid+1，mid=4，即low=mid+1=4+1=5，改变后的mid=⌊(low+high)/2 ⌋=⌊10/2⌋=⌊5⌋=5，所以结点4的右子树为5，如下：
  
  
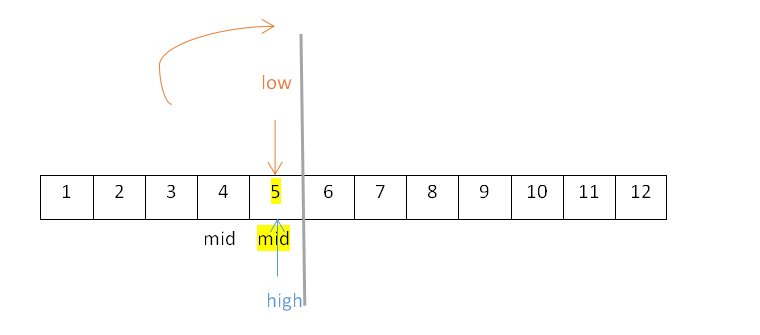
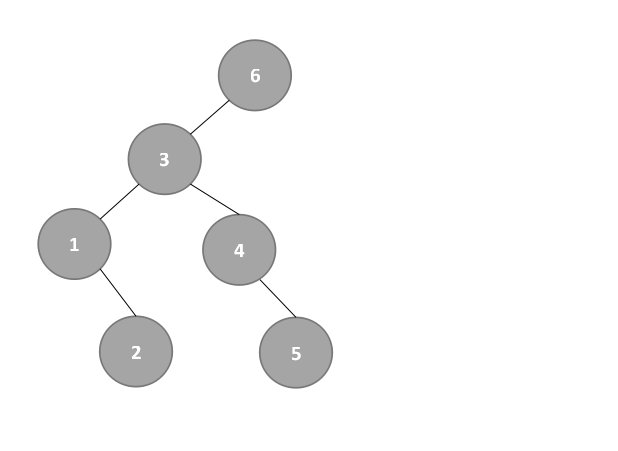
  ④mid右子表查找：
• 此时high=12不变，low为mid+1，mid=6，即low=mid+1=6+1=7，改变后的mid=⌊(low+high)/2 ⌋=⌊19/2⌋=⌊9.5⌋=9，如下：
  
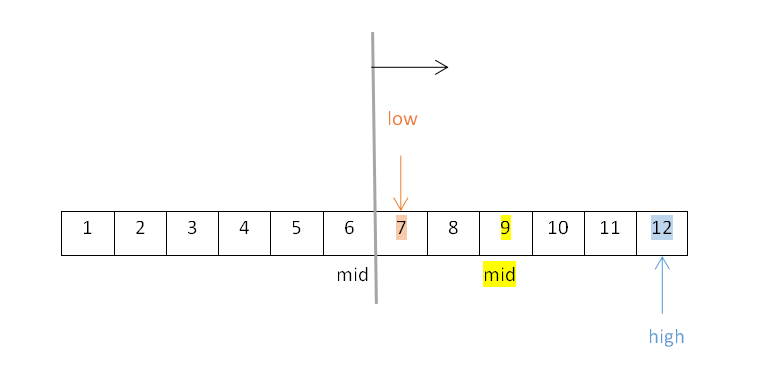
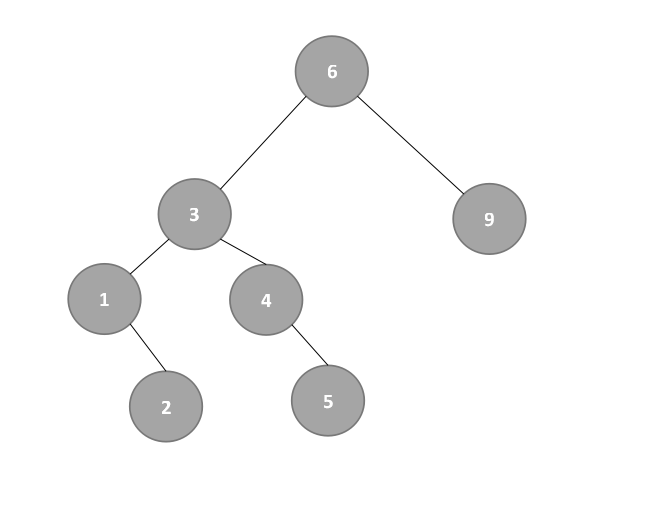
• 此时从结点9开始探索左子树，low=5不变，high为mid+1，mid=9，即high=mid+1=9+1=10，改变后的mid=⌊(low+high)/2 ⌋=⌊15/2⌋=⌊7.5⌋=7，如下：
  
  
  ……
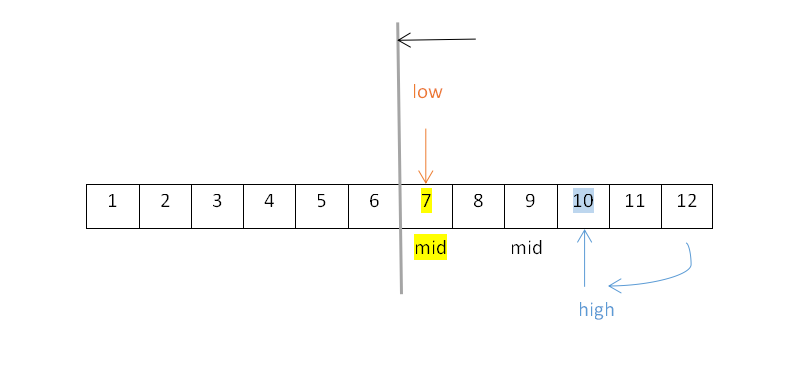
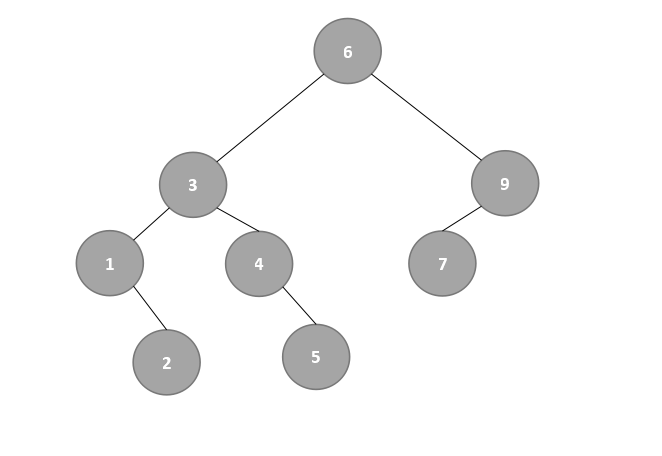
  最后可以得到如下：
  

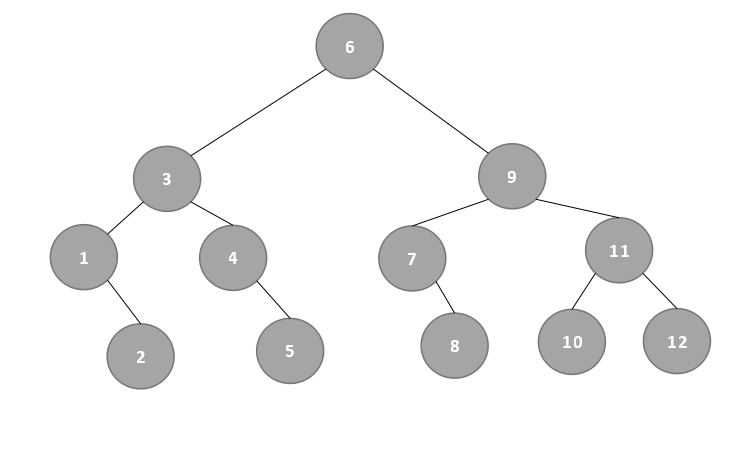
（2）查找成功：ASL=（1×1+2×2+4×3+5×4）/12=37/12。
查找失败：判定树中，将其补全，第四行失败的叶结点有3个，第五行失败的叶结点有10个，如下：

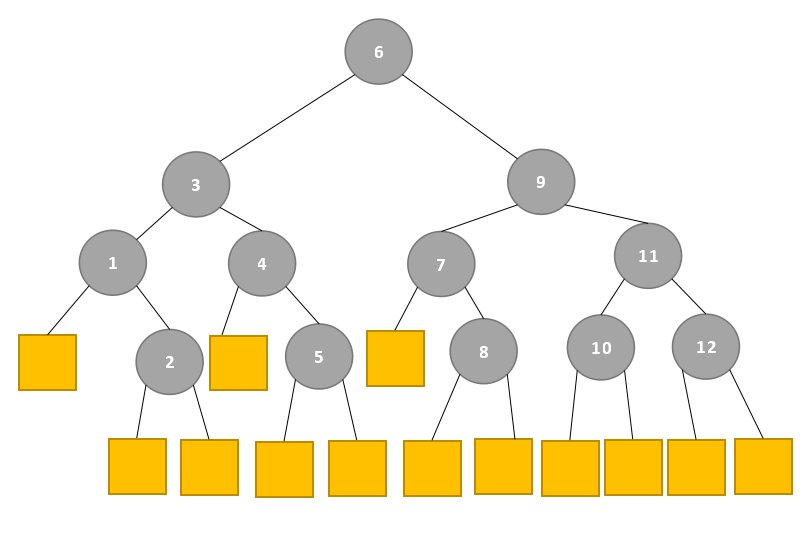
ASL=（3×3+4×10）/13=49/13。