有三块 二维矩阵 如下

把二维矩阵堆叠起来,就是三维 矩阵
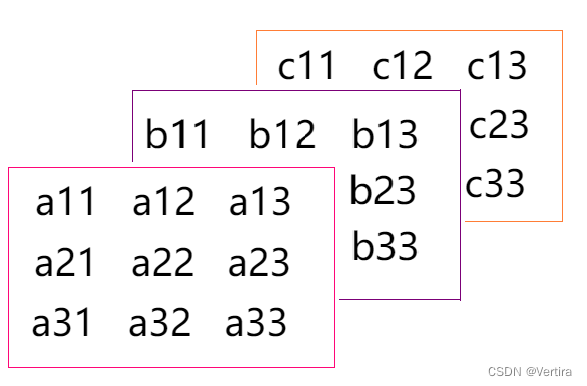
这样的矩阵 从x方向看(0维) 有三块 记为3,每块从y方向看(1维)的行是3,从z方向看(2维)列也是3,故三维矩阵的尺寸就是(3,3,3)
permute(dims)是干啥的, 它是操作维度的,二维是转置,原三维不变的情况下(0,1,2),可以变(0,2,1),就是转置了
permute(dims)
- 参数dims用矩阵的维数代入,一般默认从0开始。即第0维,第1维等等
- 也可以理解为,第0块,第1块等等。当然矩阵最少是两维才能使用permute
- 如是两维,dims分别为是0和1
- 可以写成permute(0,1)这里不做任何变化,维数与之前相同
- 如果写成permute(1,0)得到的就是矩阵的转置
- 如果三维是permute(0,1,2)
- 0代表共有几块维度:本例中0对应着3块矩阵
- 1代表每一块中有多少行:本例中1对应着每块有2行
- 2代表每一块中有多少列:本例中2对应着每块有5列
- 所以是3块2行5列的三维矩阵
- 这些0,1,2并没有任何实际的意义,也不是数值,只是用来标识区别。有点类似于x,y,z来区分三个坐标维度,是人为规定好的
- 三维情况直接用下面的代码来给大家讲解
举例:
>>> x2 = torch.linspace(1, 30, steps=30).view(3,2,5) #产生30个数,步长30,把这30个数组成x方向3块,每一快 y方向2个数,z方向5个数
>>> x2
tensor([[[ 1., 2., 3., 4., 5.],[ 6., 7., 8., 9., 10.]],[[11., 12., 13., 14., 15.],[16., 17., 18., 19., 20.]],[[21., 22., 23., 24., 25.],[26., 27., 28., 29., 30.]]])
>>>变化一:不改变任何参数
>>> b = x2.permute(0,1,2) # b和x2矩阵一样
>>> b
tensor([[[ 1., 2., 3., 4., 5.],[ 6., 7., 8., 9., 10.]],[[11., 12., 13., 14., 15.],[16., 17., 18., 19., 20.]],[[21., 22., 23., 24., 25.],[26., 27., 28., 29., 30.]]])
>>>变化二:0,1交换
>>> b1 = x2.permute(1,0,2) 仔细看看b1 与b的变化
>>> b1
tensor([[[ 1., 2., 3., 4., 5.],[11., 12., 13., 14., 15.],[21., 22., 23., 24., 25.]],[[ 6., 7., 8., 9., 10.],[16., 17., 18., 19., 20.],[26., 27., 28., 29., 30.]]])变化二:1,2交换
>>> b2 = x2.permute(0,2,1)
>>> b2
tensor([[[ 1., 6.],[ 2., 7.],[ 3., 8.],[ 4., 9.],[ 5., 10.]],[[11., 16.],[12., 17.],[13., 18.],[14., 19.],[15., 20.]],[[21., 26.],[22., 27.],[23., 28.],[24., 29.],[25., 30.]]])
>>>这个函数的功能 就是转置变换,元素大小和个数不变,就是矩阵的形式变化
参考:
torch中permute()函数用法_permute函数_ac不知深的博客-CSDN博客