目录:
1.搜索二叉树的概念
2.对搜索二叉树实现插入Insert函数和InOrder中序遍历函数
3.删除
4.实现搜索二叉树的递归
5.拷贝问题
6.搜索二叉树的缺陷
--------------------------------------------------------------------------------------------------------------------------------
1.搜索二叉树的概念
搜索二叉树又称二叉排序树,它或者是一颗空树
特征:1.若它的左子树不为空,则左子树上所有节点的值都小于跟节点的值
2.若它的右子树不为空,则右子树上所有节点的值都大于跟节点的值
3.它的左右子树也分别为二叉搜索树
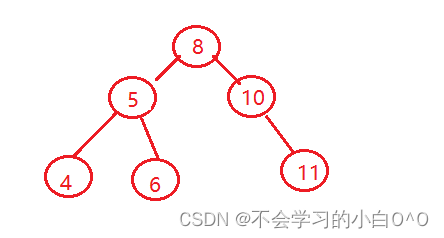
如果我要查找6 ---->最多查找高度次
为什么又叫二叉排序树呢???
我们对上面的树走一个中序遍历(先遍历左树,在遍历根,在遍历右树)
4 --> 5 ----> 6 --->8 ---->10---->11
------------------------------------------------------------------------------------------------------------
2.对搜索二叉树实现插入Insert函数
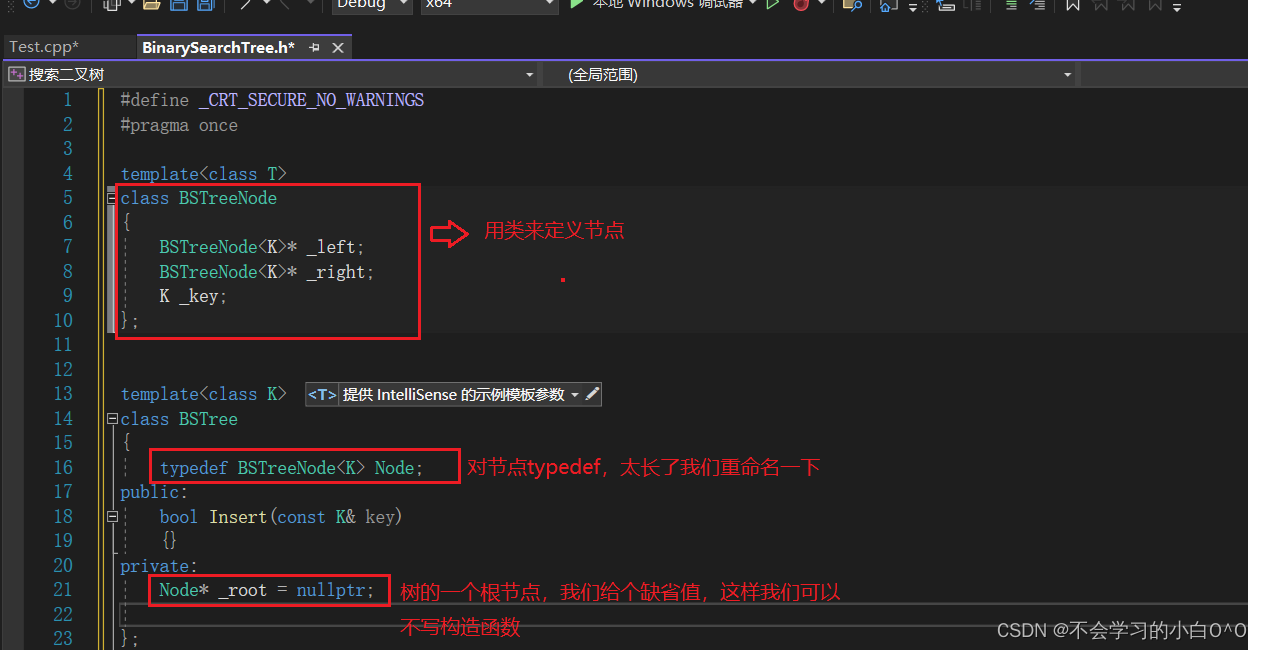
我们先简单的实现一个Insert插入函数
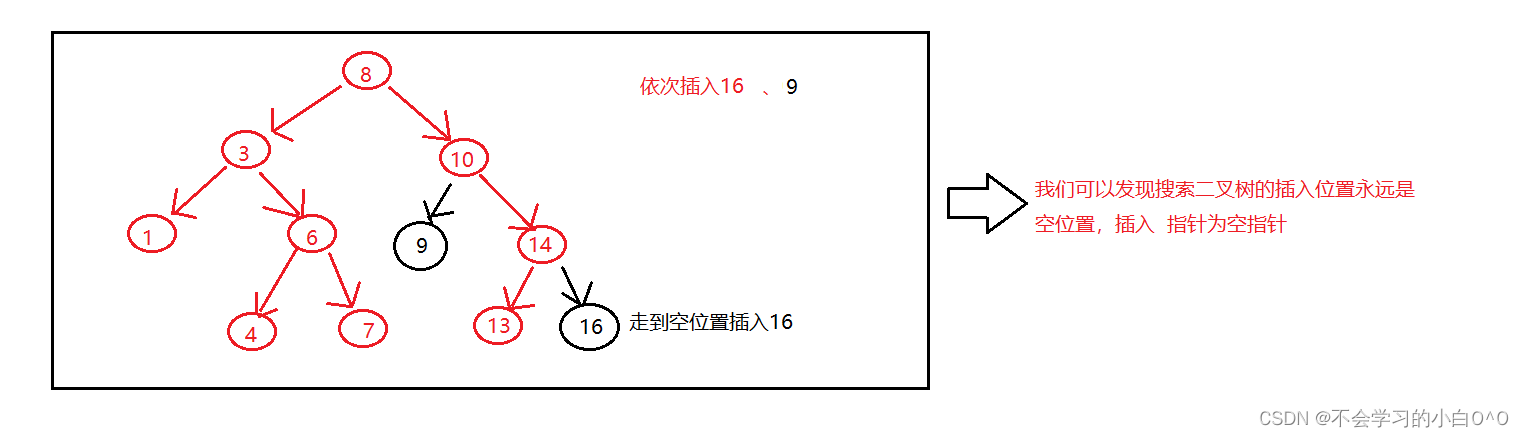
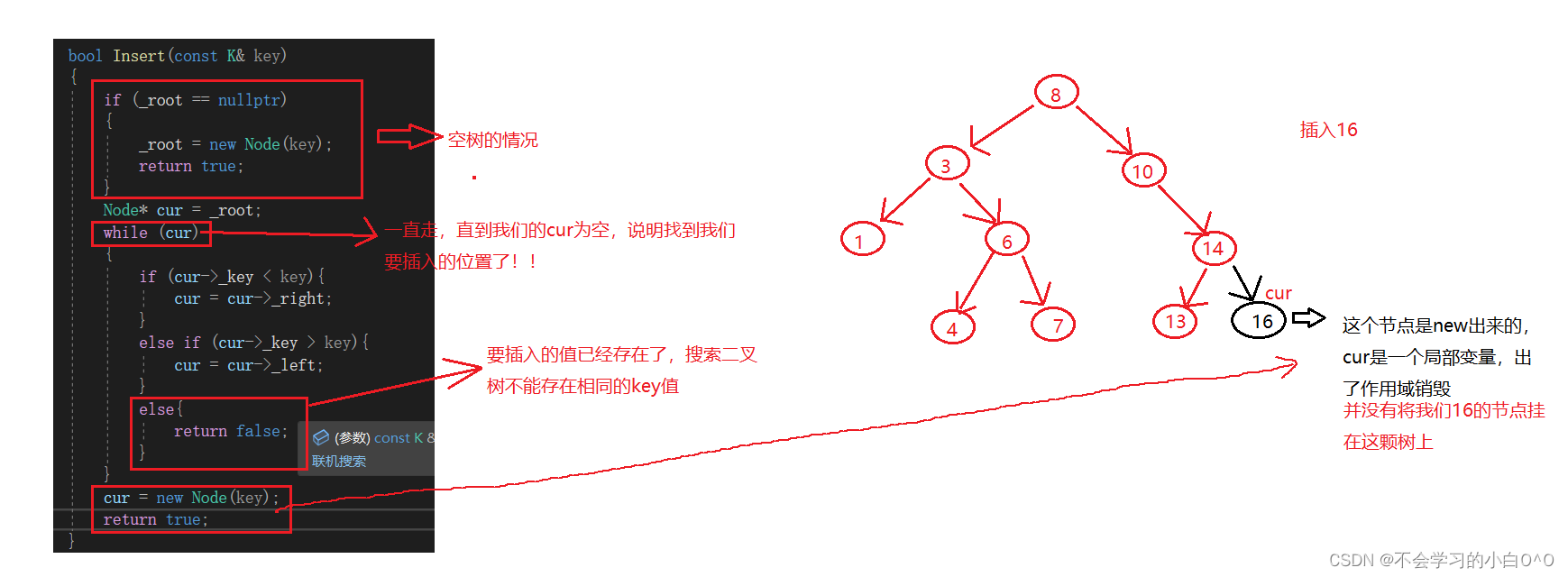
这时候我们还需要在最后找到了插入的位置时,new出来的节点,前后连接一下,找到这个空节点的父亲
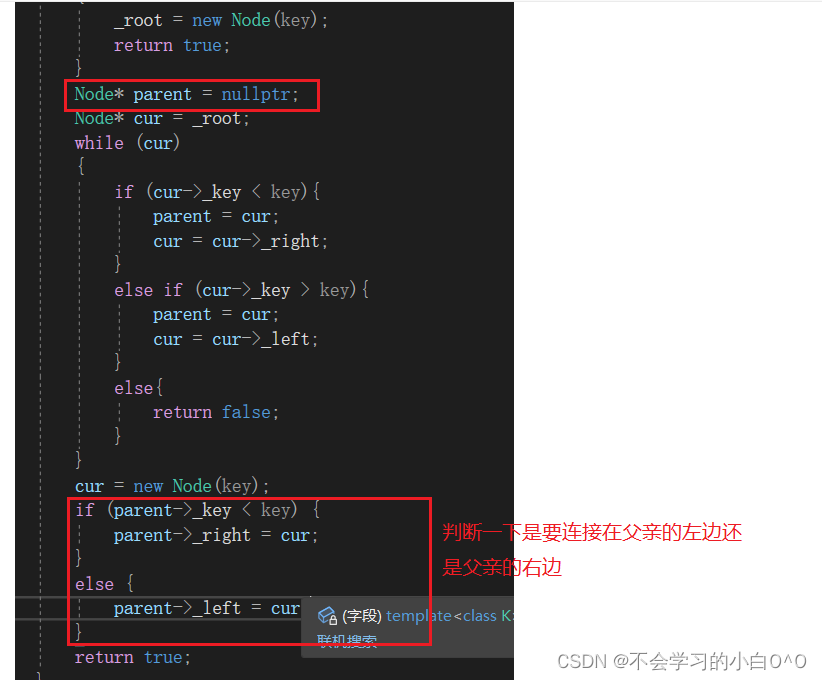
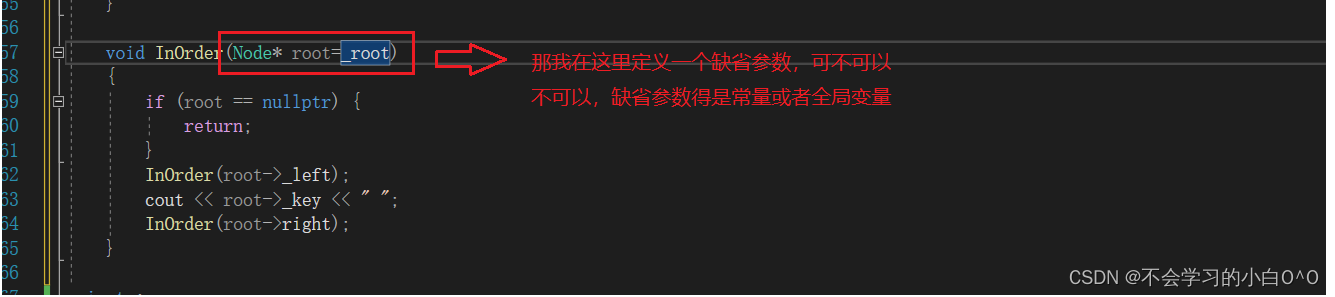
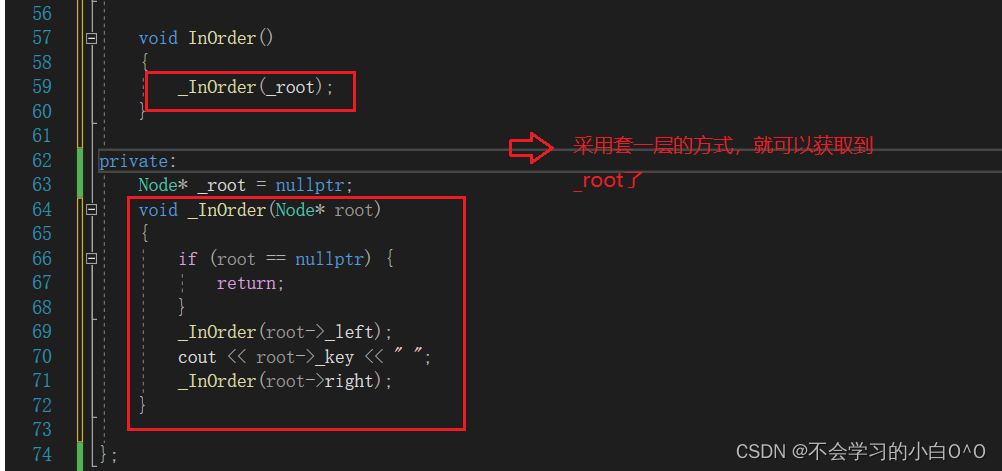
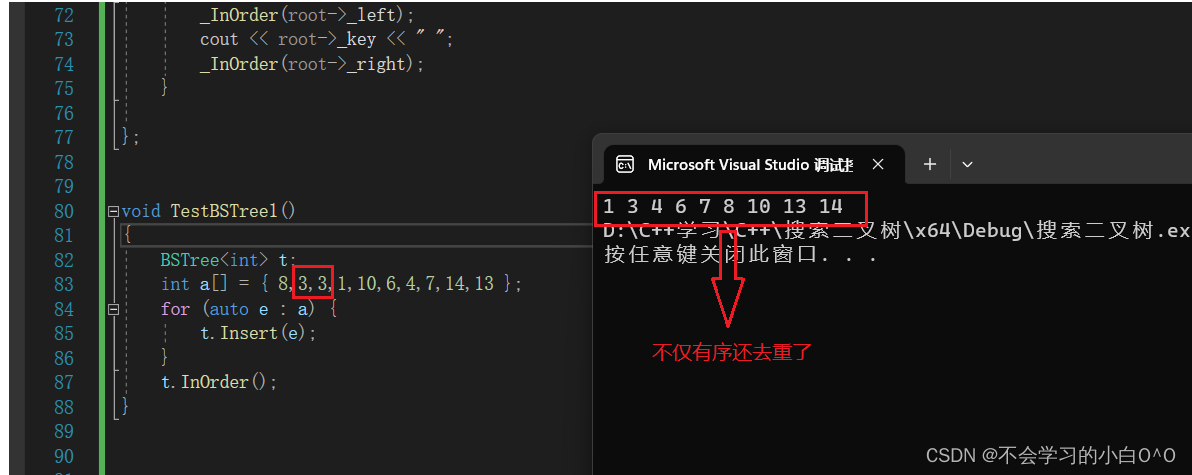
InOrder中序遍历
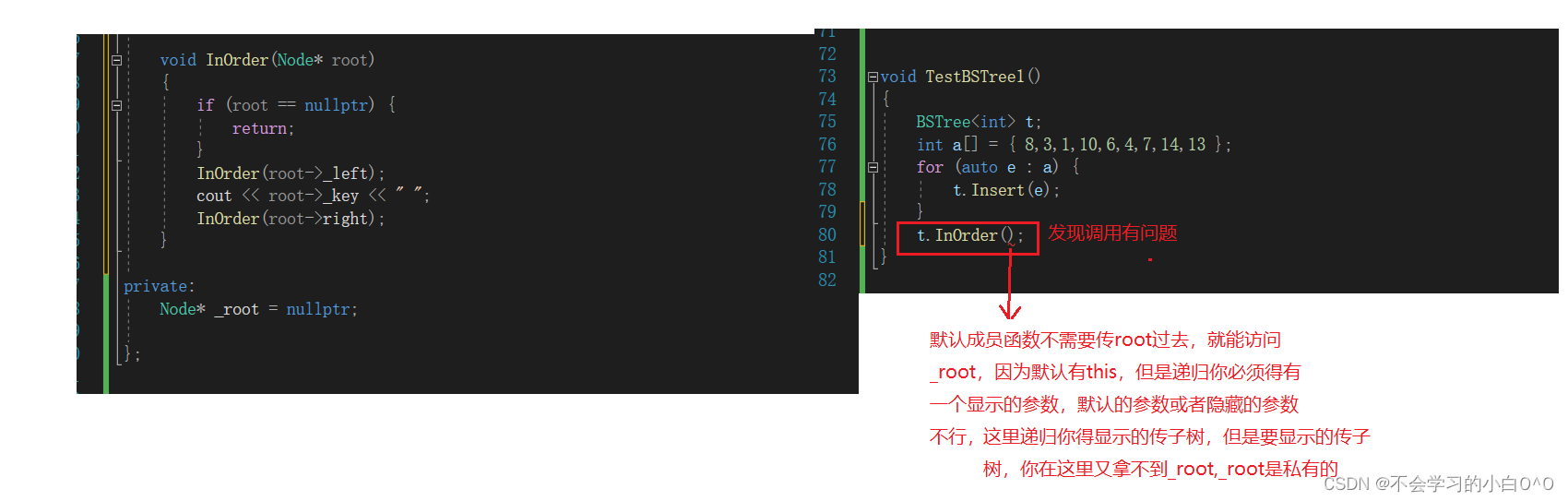
怎么解决呢???
查找函数Find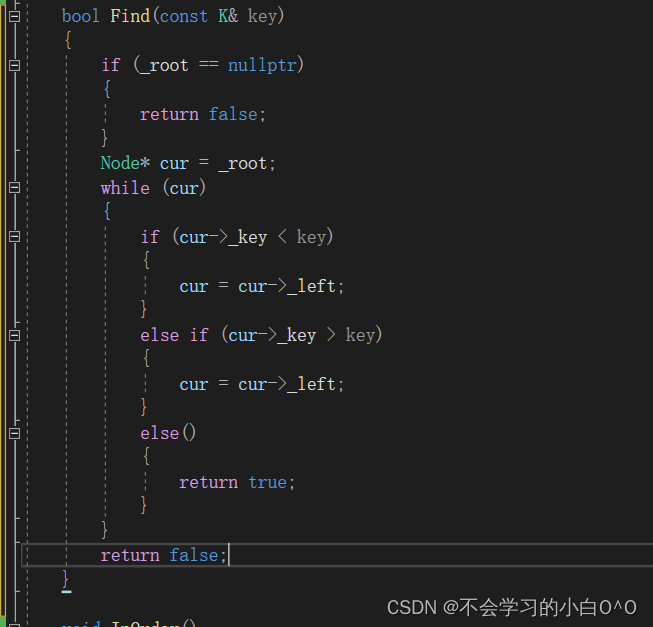
-------------------------------------------------------------------------------------------------------------------------
3.删除
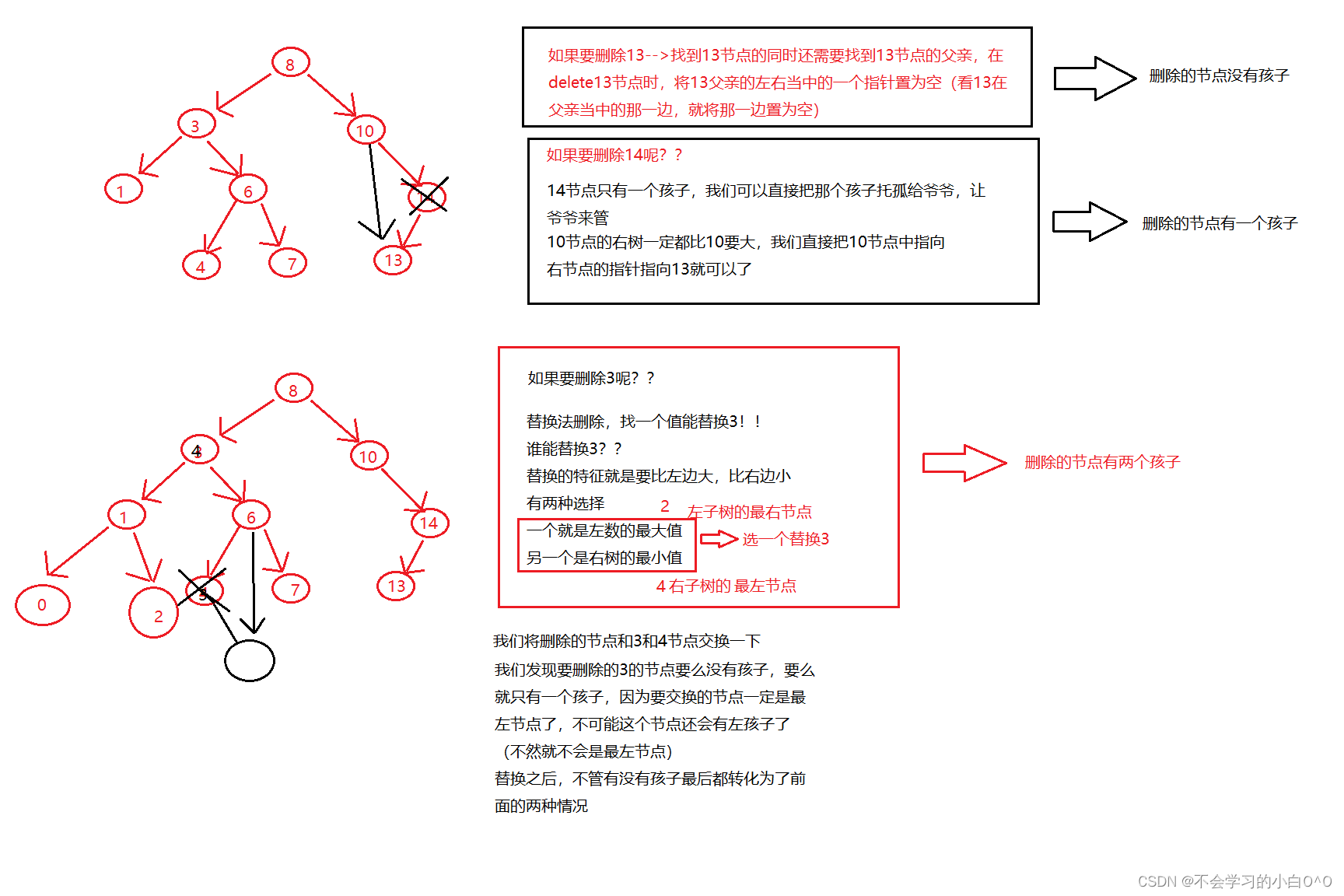
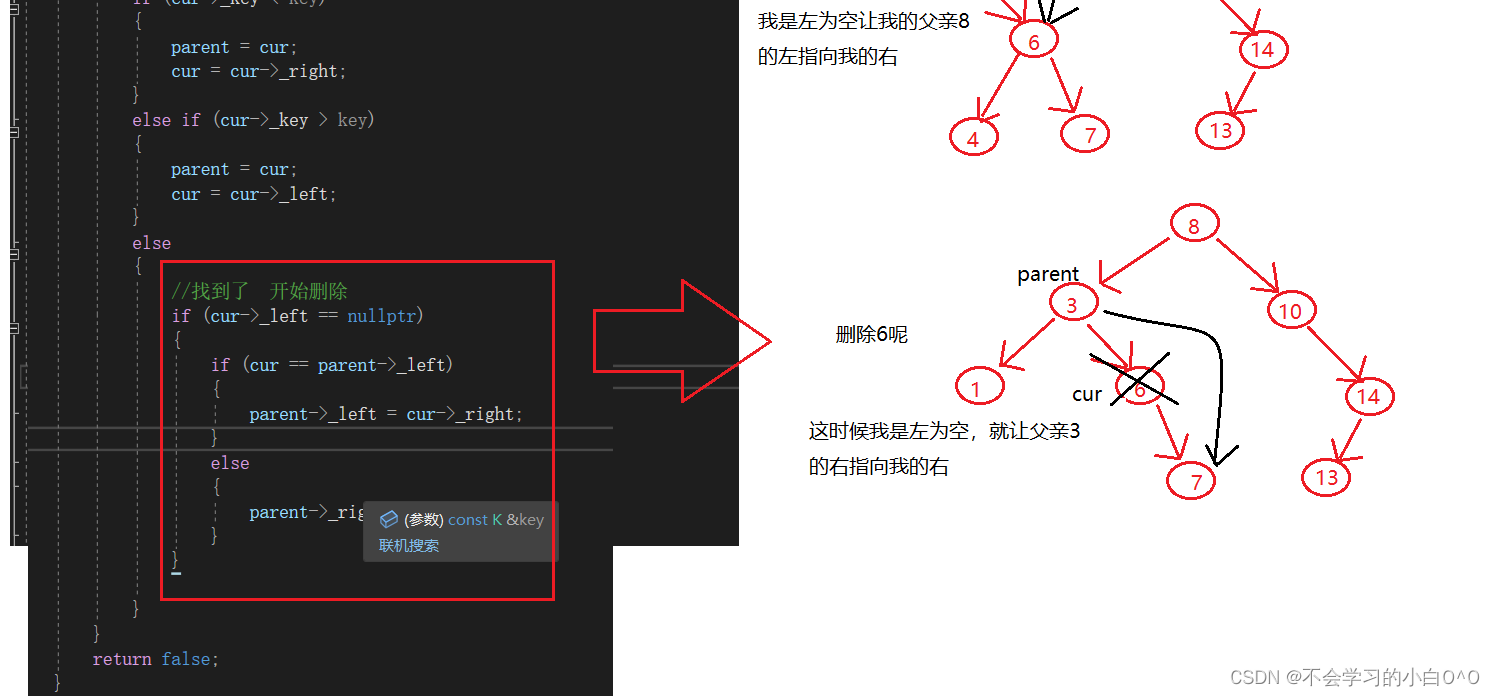
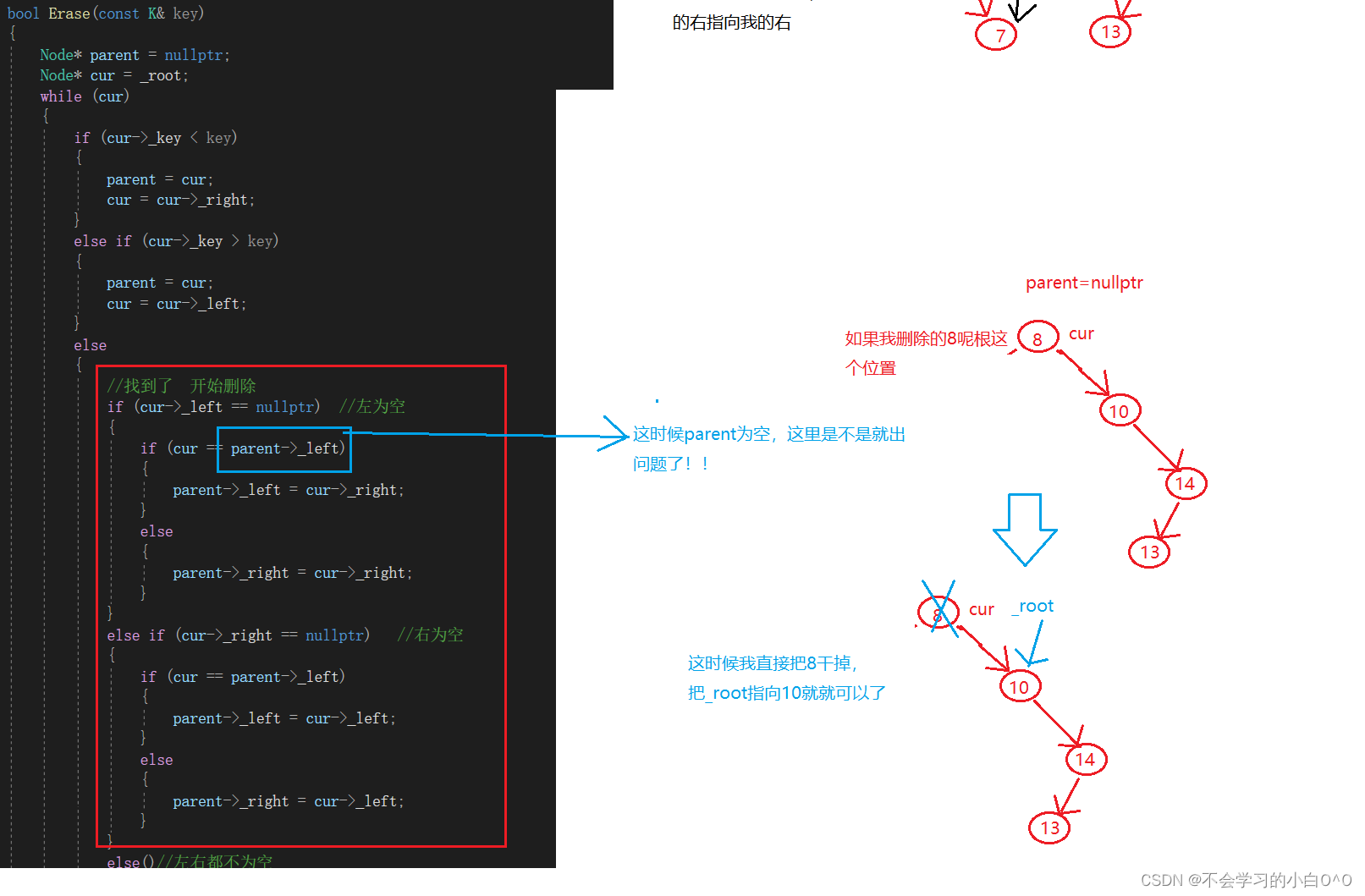
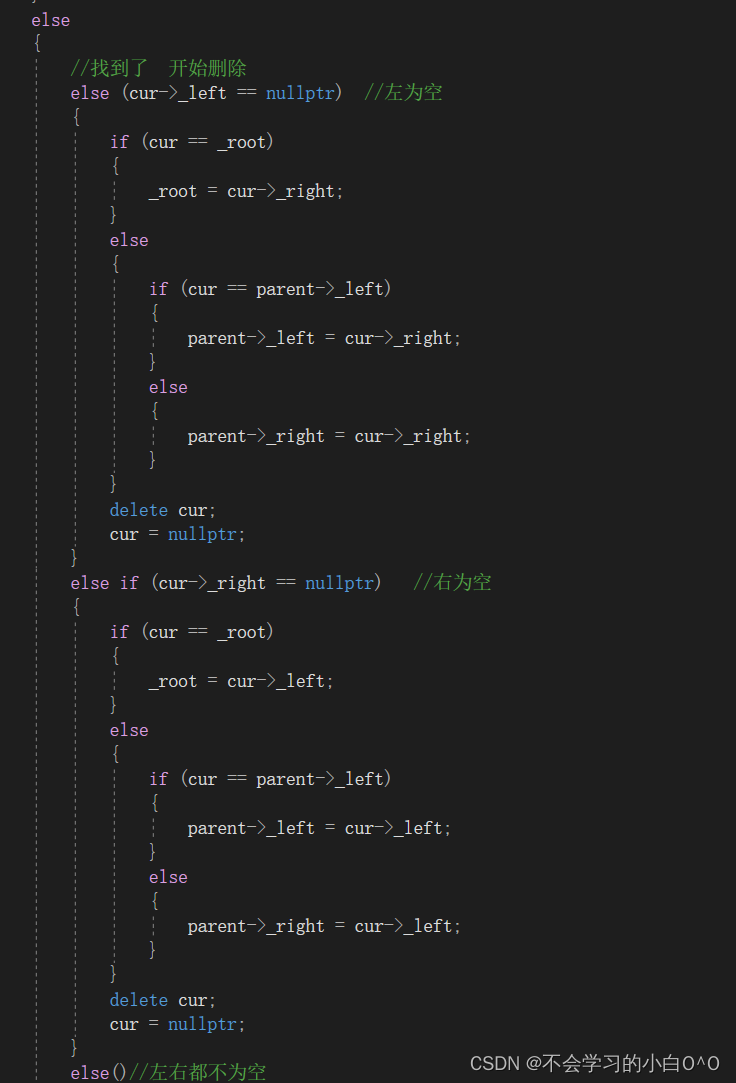
我们现在来看最后一个情况 --》 左右都不为空
我们统一用删除节点的右子树最小值来删除
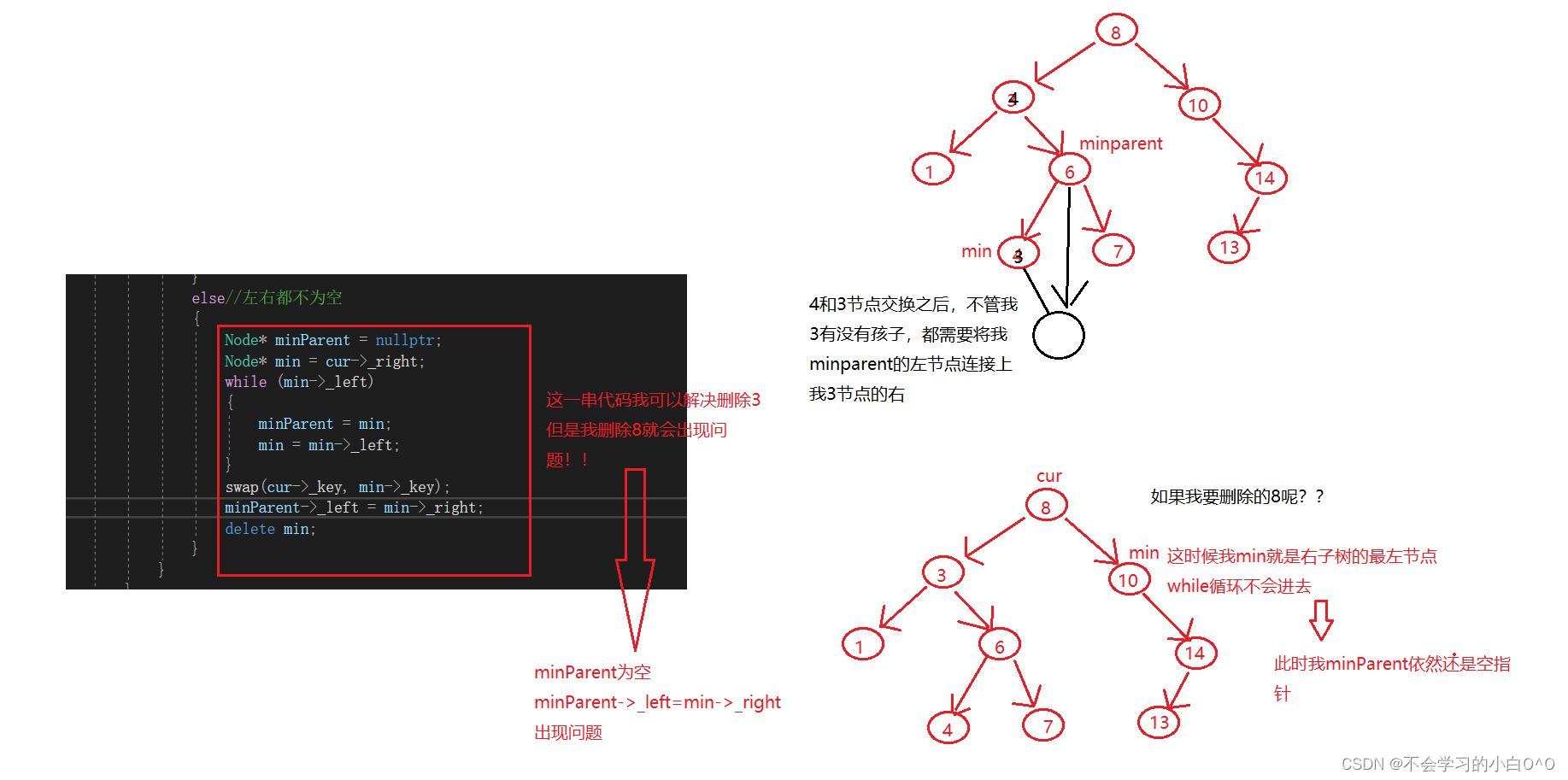
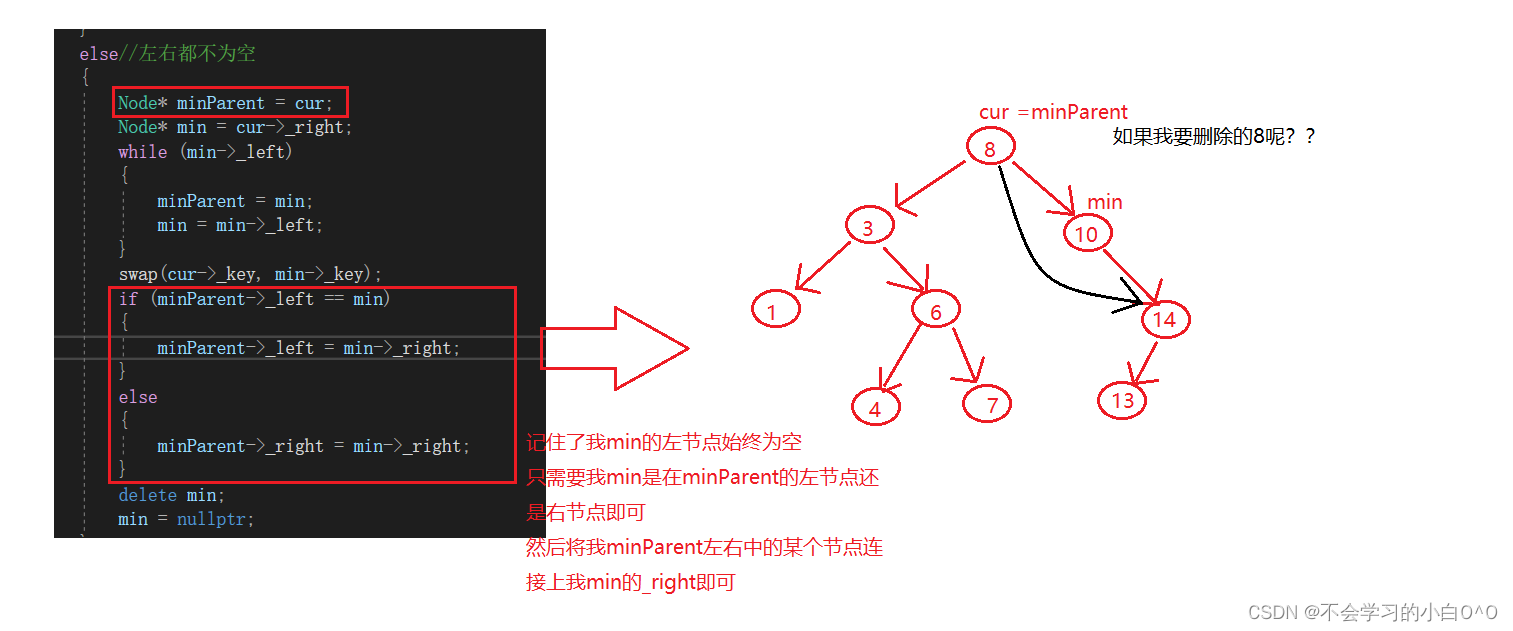
我们来验证一下Erase
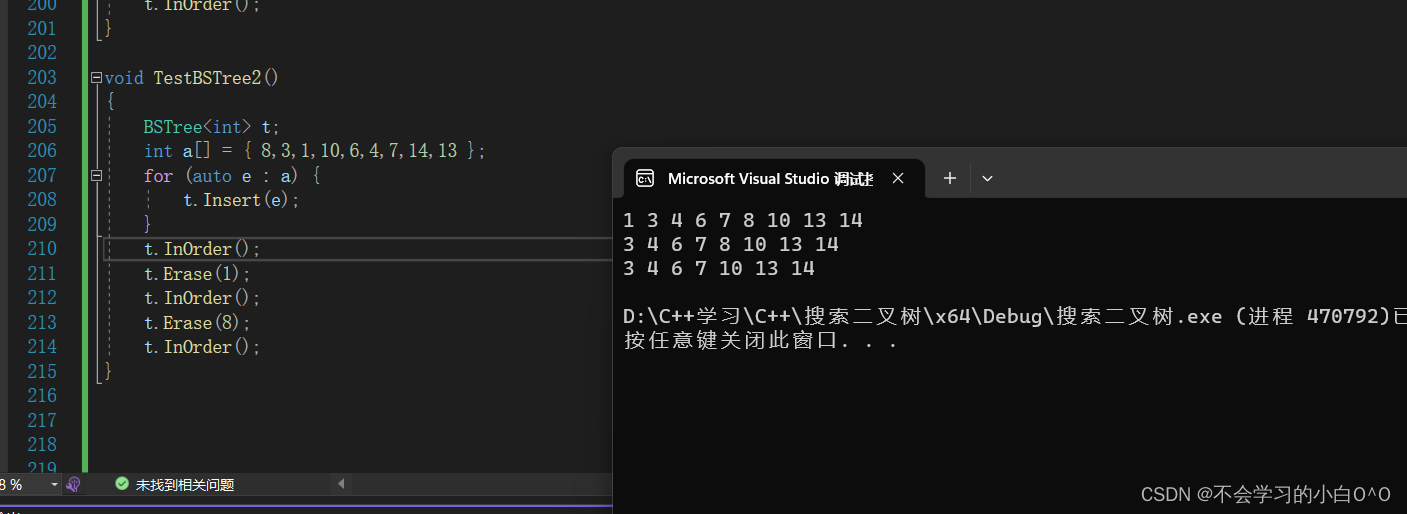
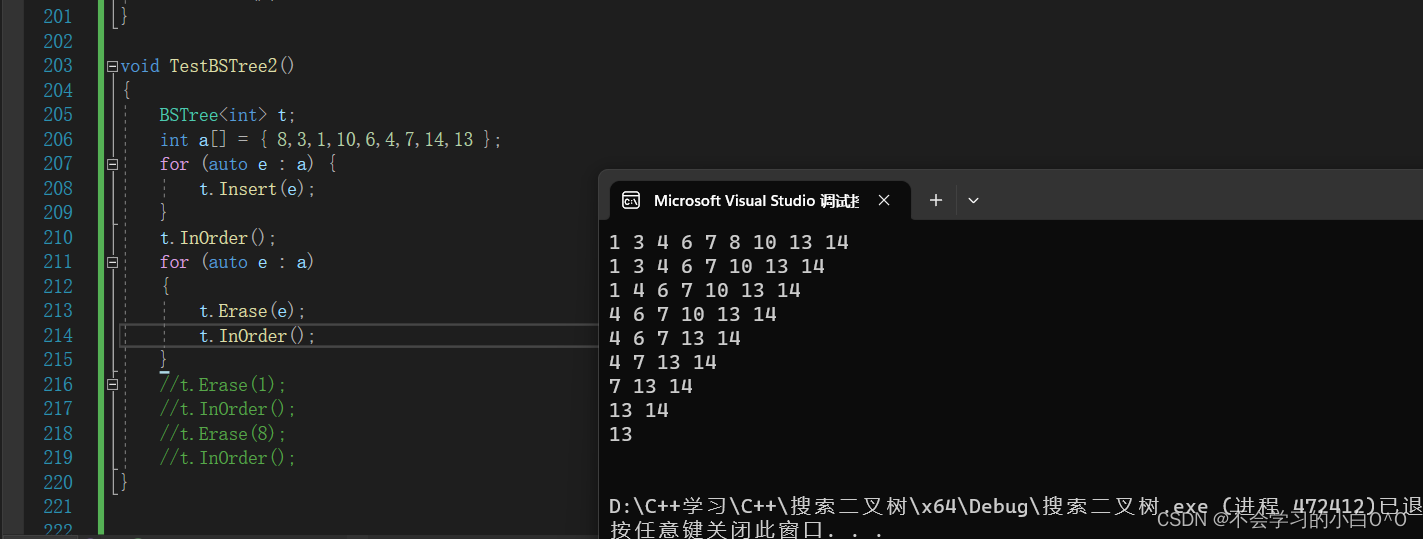
--------------------------------------------------------------------------------------------------------------------
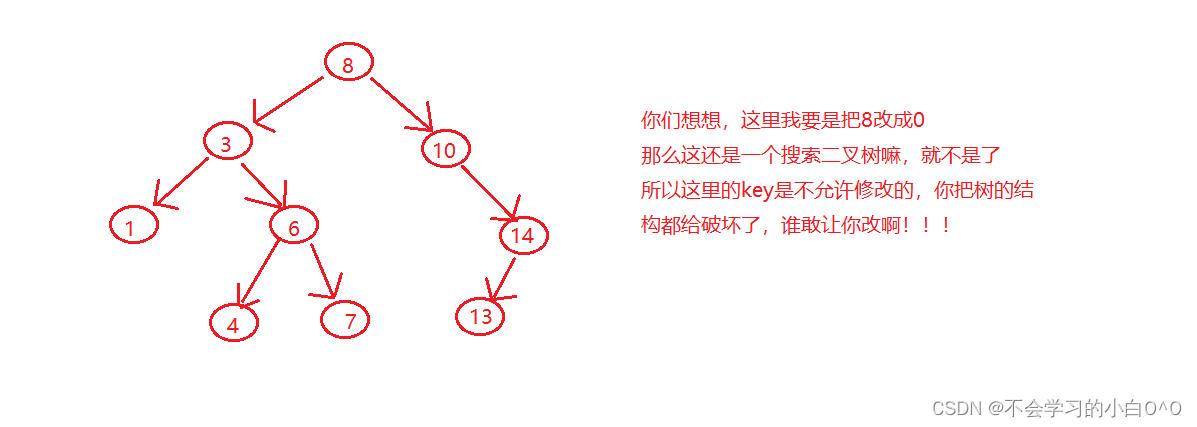
我们现在完成了搜索二叉树的增删查
我们想像搜索二叉树为什么不支持改呢??
------------------------------------------------------------------------------------------------------------------------
4.实现搜索二叉树的循环
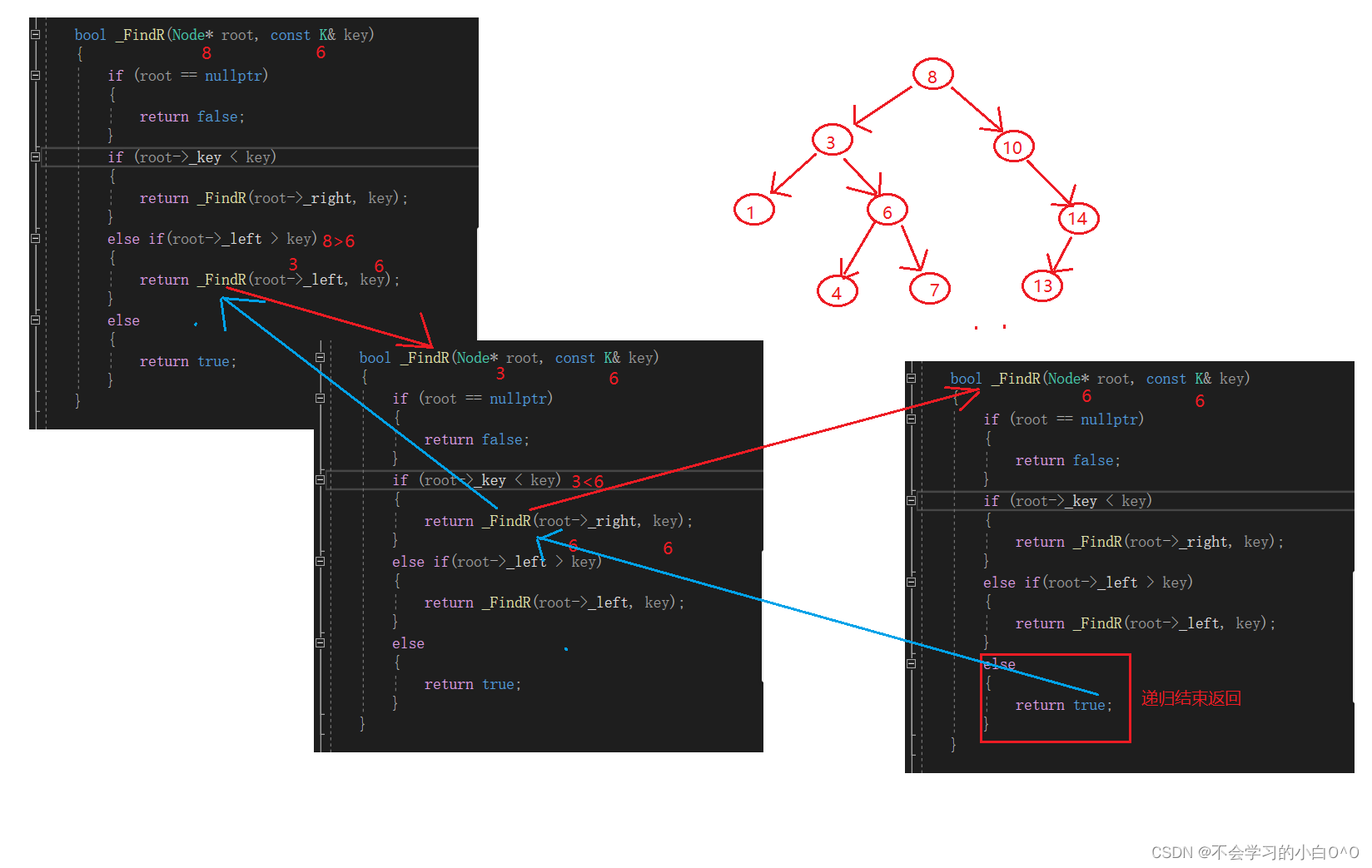
1.先实现一个递归查找

假如我们在这里要找的值是6,我们来看看递归是怎么找的
-------------------------------------------------------------------------------------------------------------------------------
插入递归的实现!!!
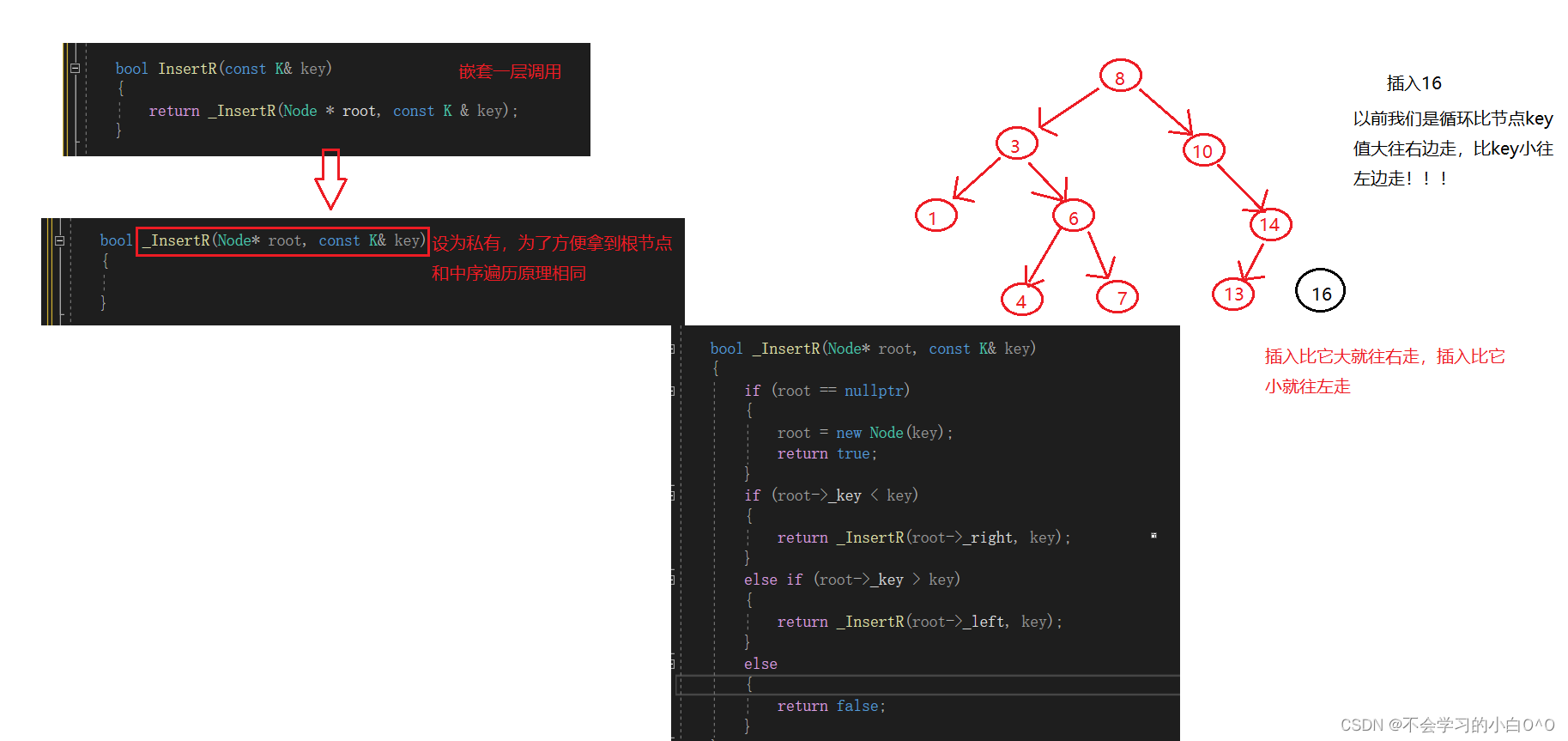
这样子可以完成我们的插入嘛,我们来走走看
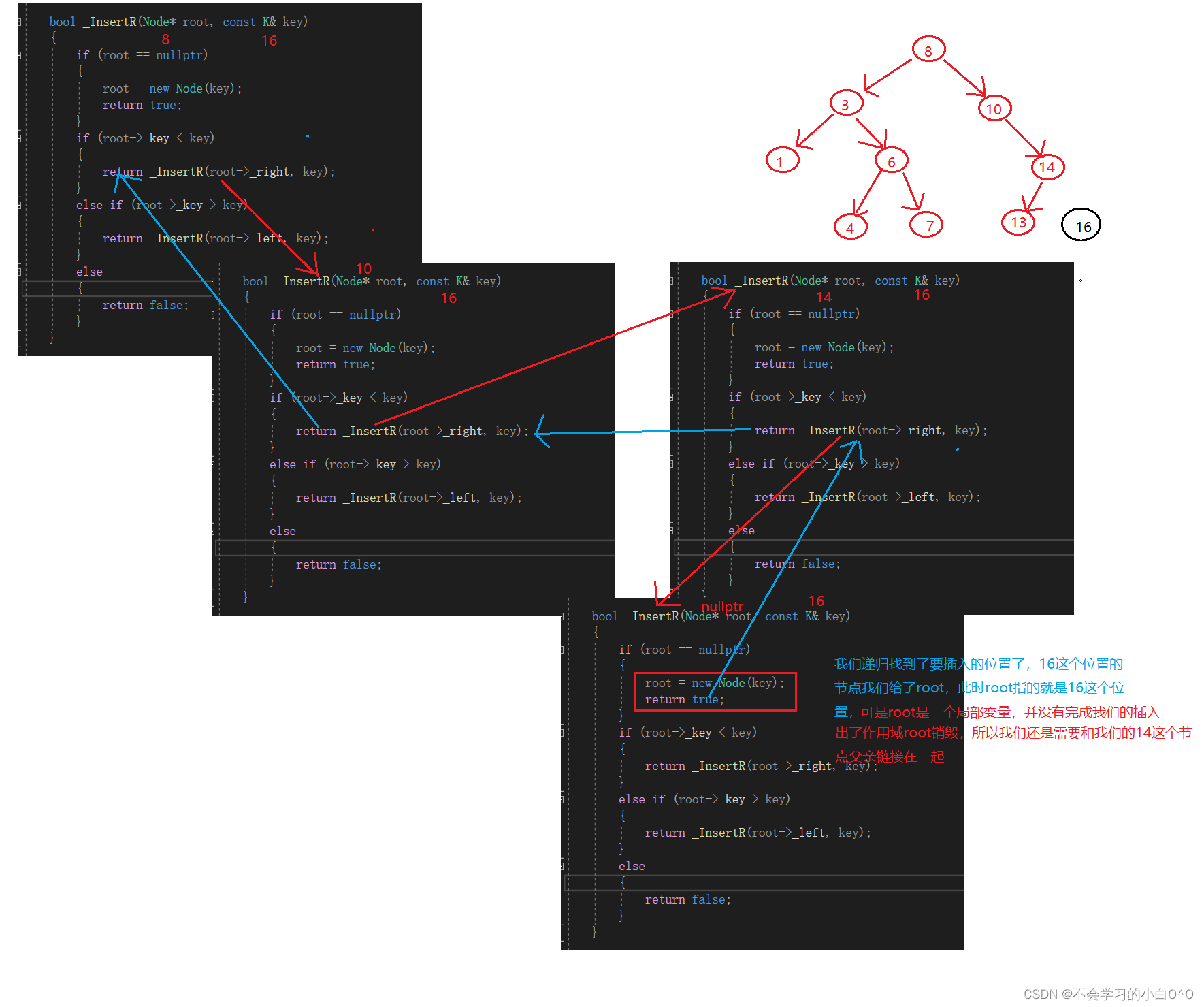
可是我们怎么巧妙的和父亲链接在一起呢???当然我们也可以把父亲传下去,这个是最普通的做法了,我们可以有更巧妙的做法
我们加个引用来看看 ---- 前面的引用都不起作用,只有在最后一下
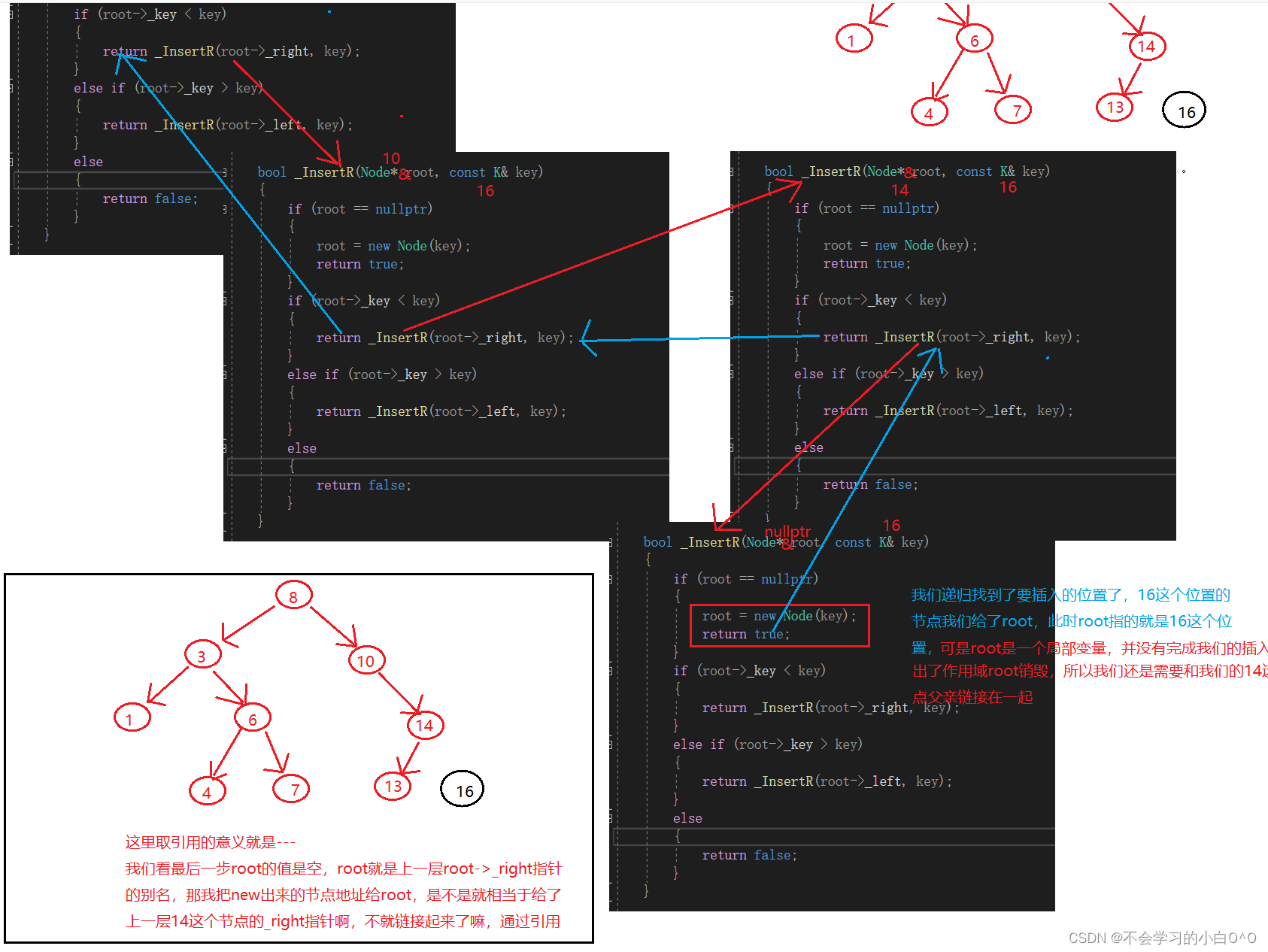
---------------------------------------------------------------------------------------------------------------------------
我们现在来实现一下递归删除
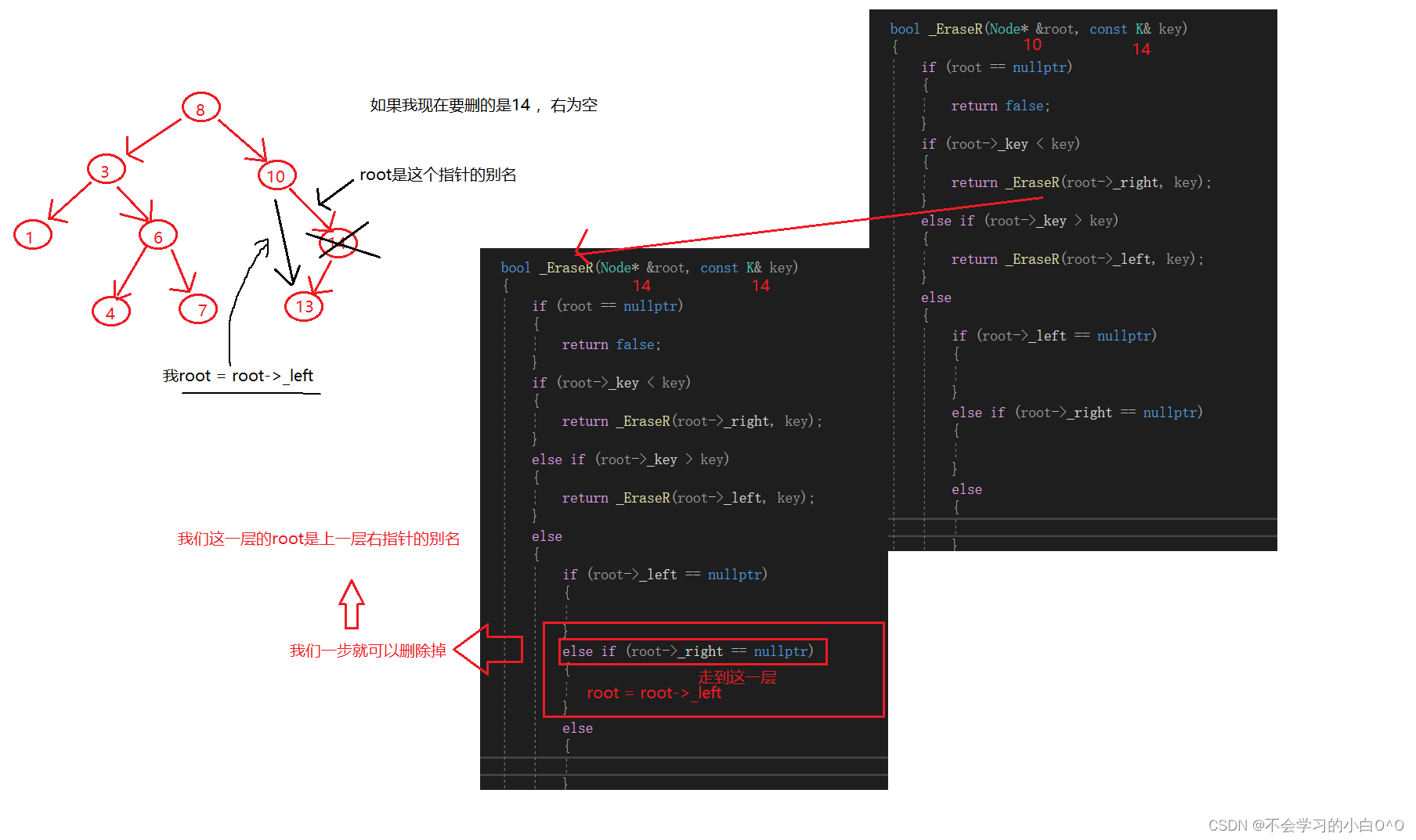

如果我们删除左右都不为空的呢???
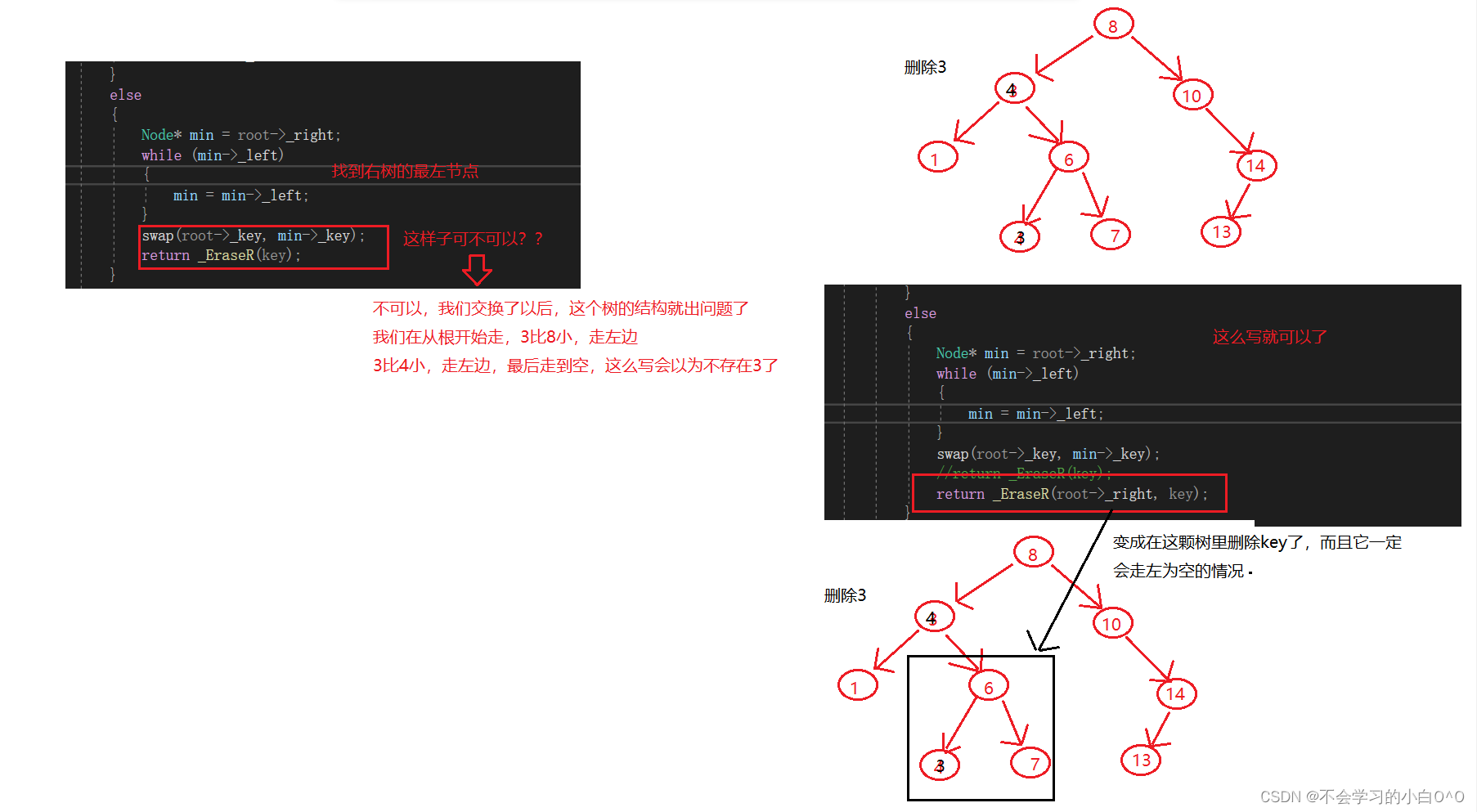
-------------------------------------------------------------------------------------------------------------------------------
5.拷贝问题
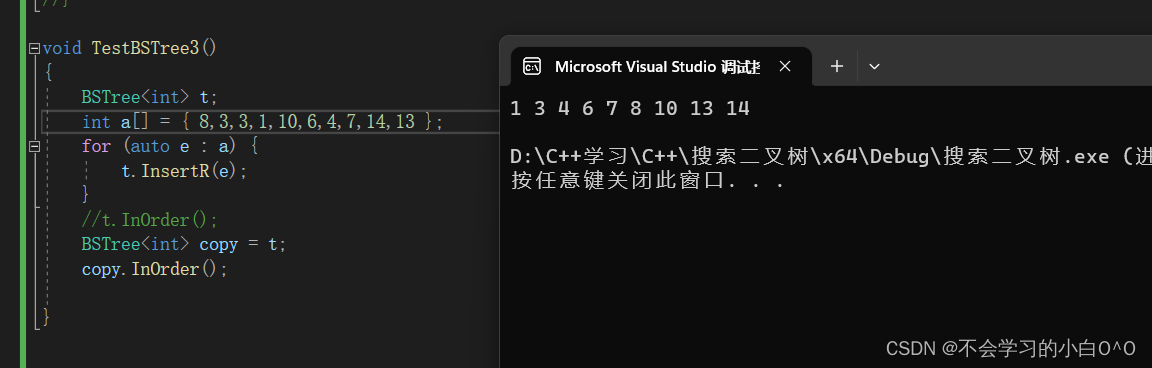
我们拷贝了之后发现是没有问题的,可是实际上是有问题的
我们还没有写拷贝构造,那么这里就是浅拷贝,浅拷贝针对于内置类型默认生成的是浅拷贝
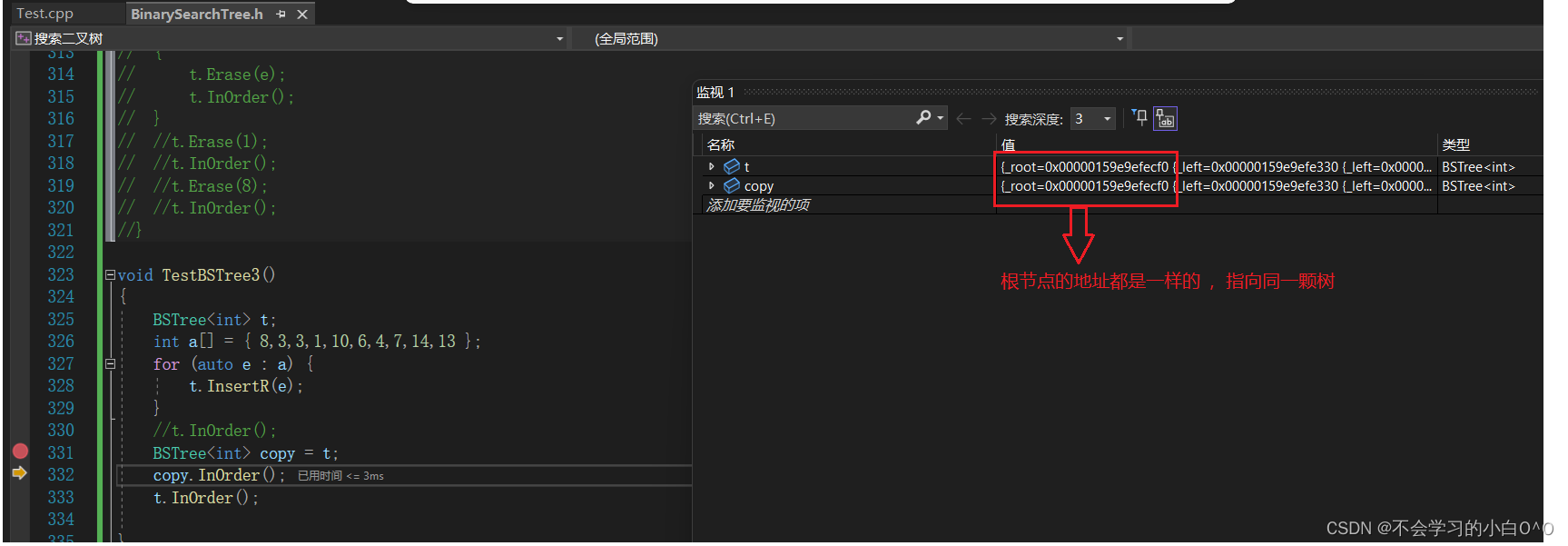
现在没崩的原因是没写析构
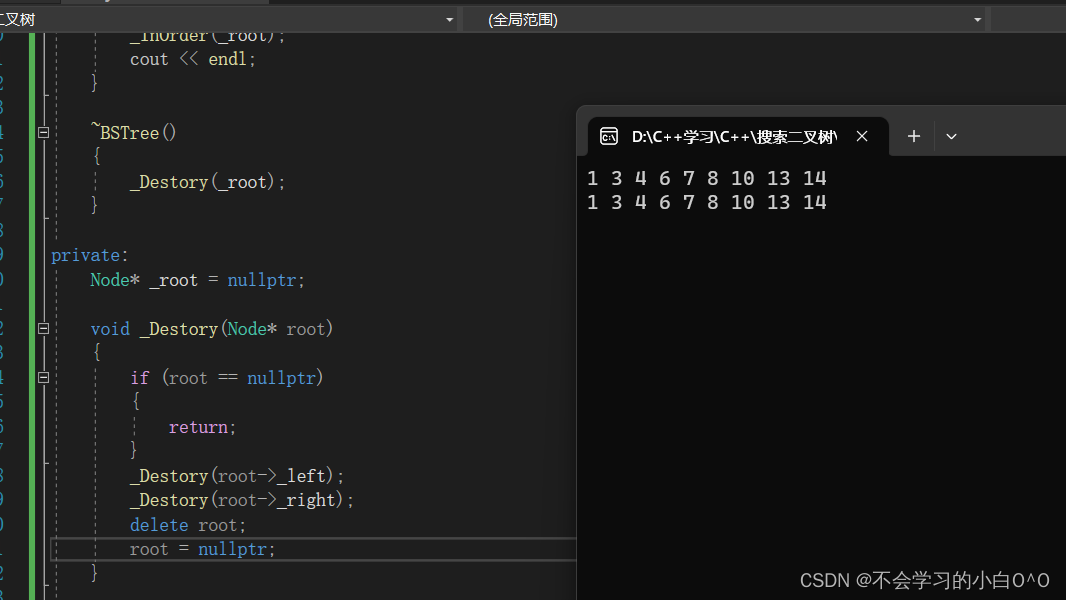
这时候就会出现野指针的问题了,就是由于浅拷贝导致的
那么我们应该这么进行深拷贝呢??
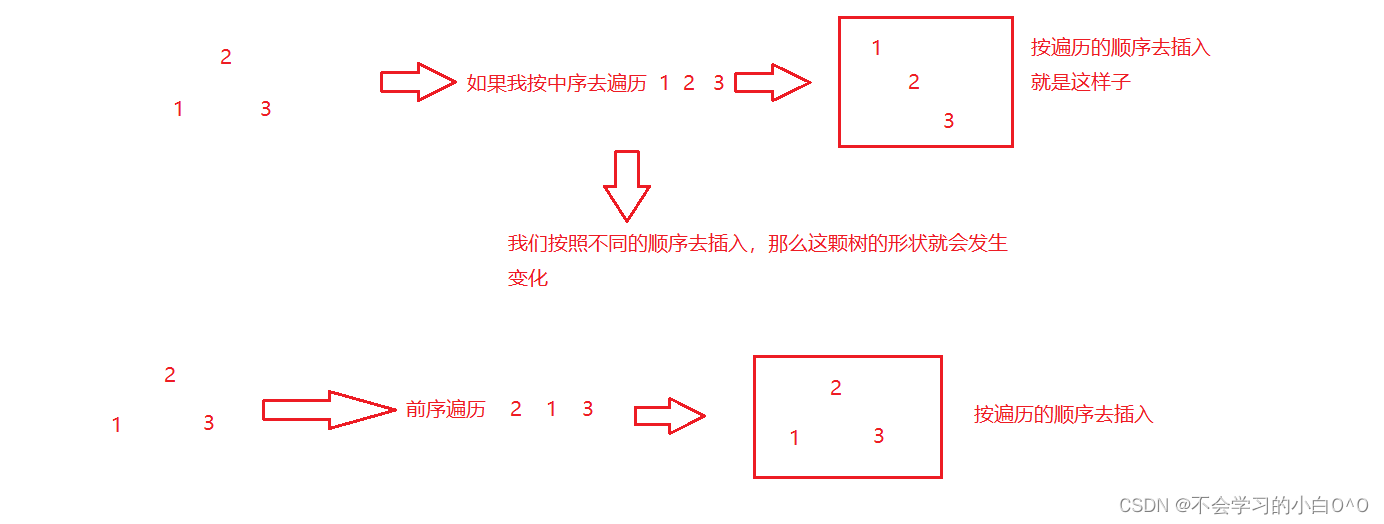
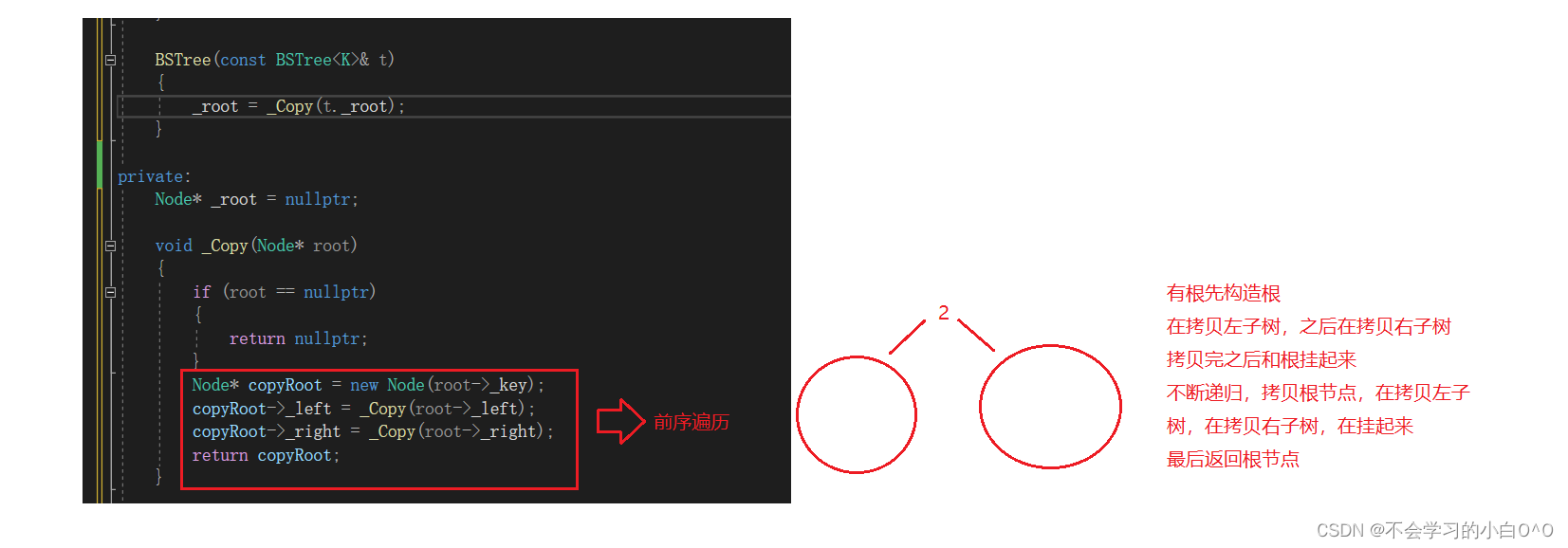
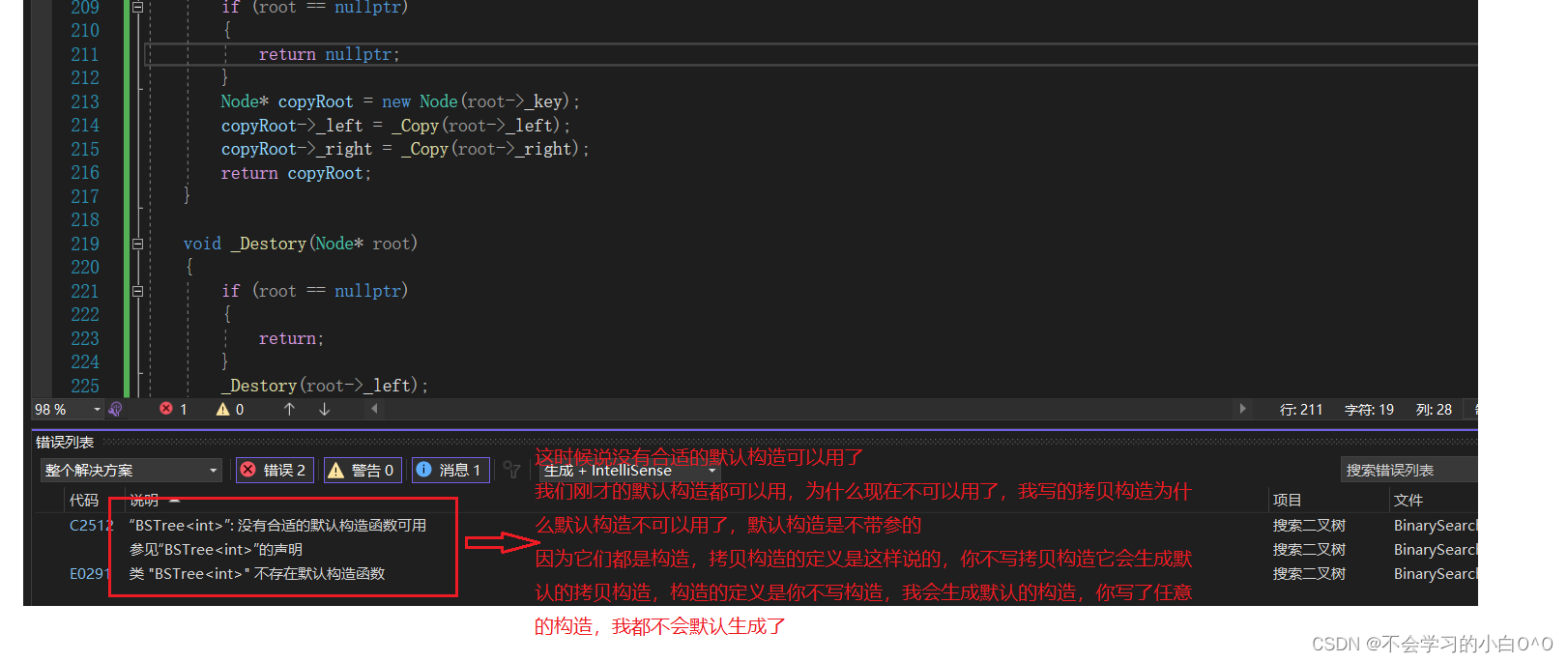
这时候我们自己写一个默认的构造
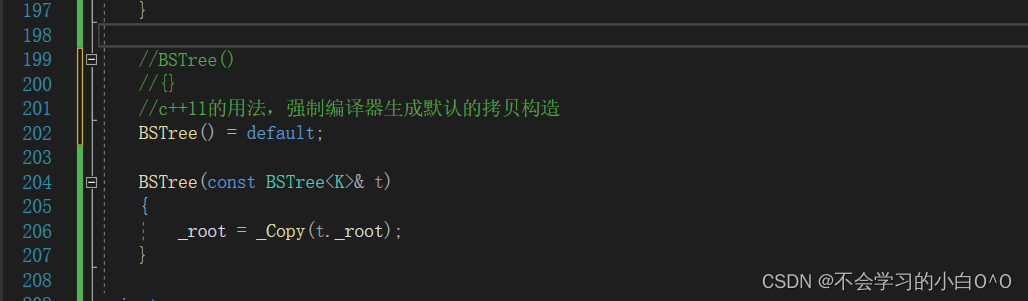
这时候就没有问题了
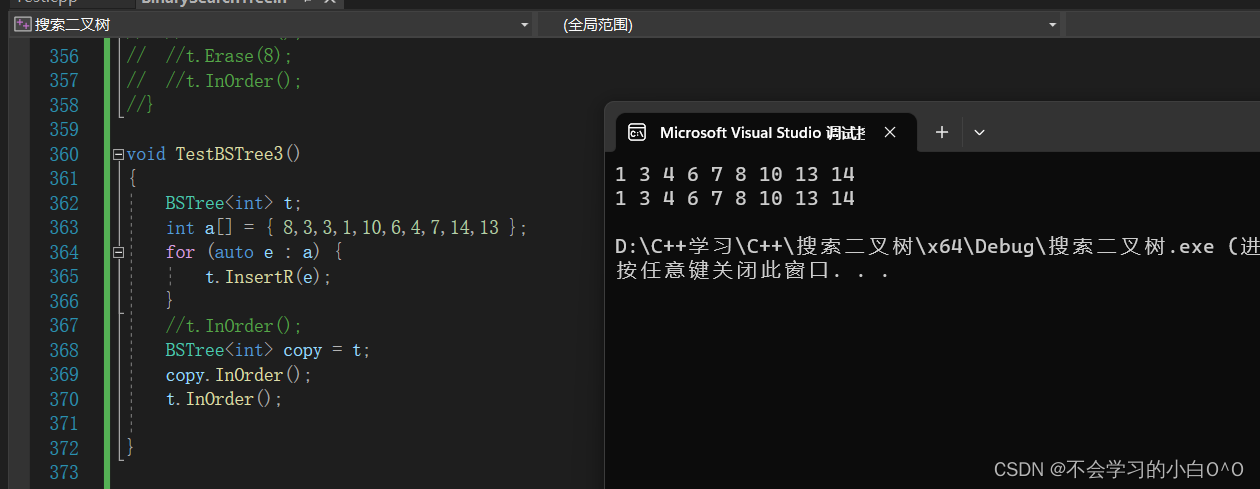
那么赋值呢??
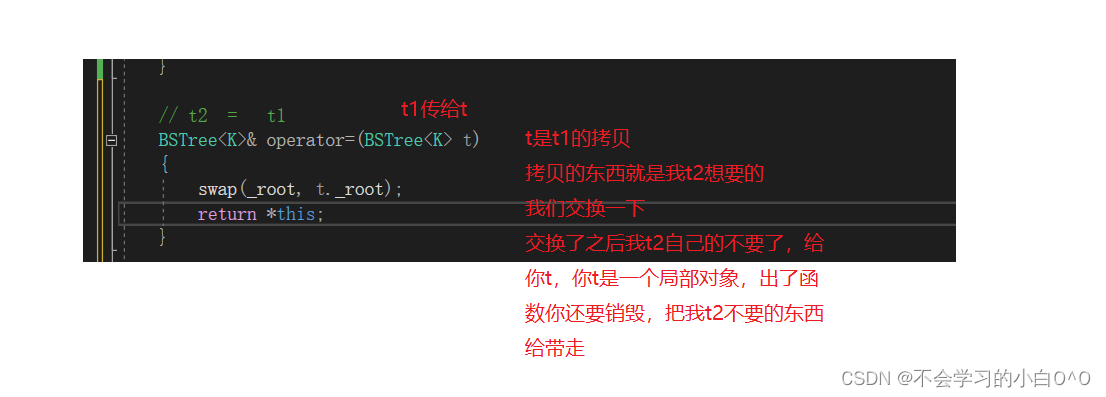
------------------------------------------------------------------------------------------------------------------------
6.搜索二叉树的缺陷
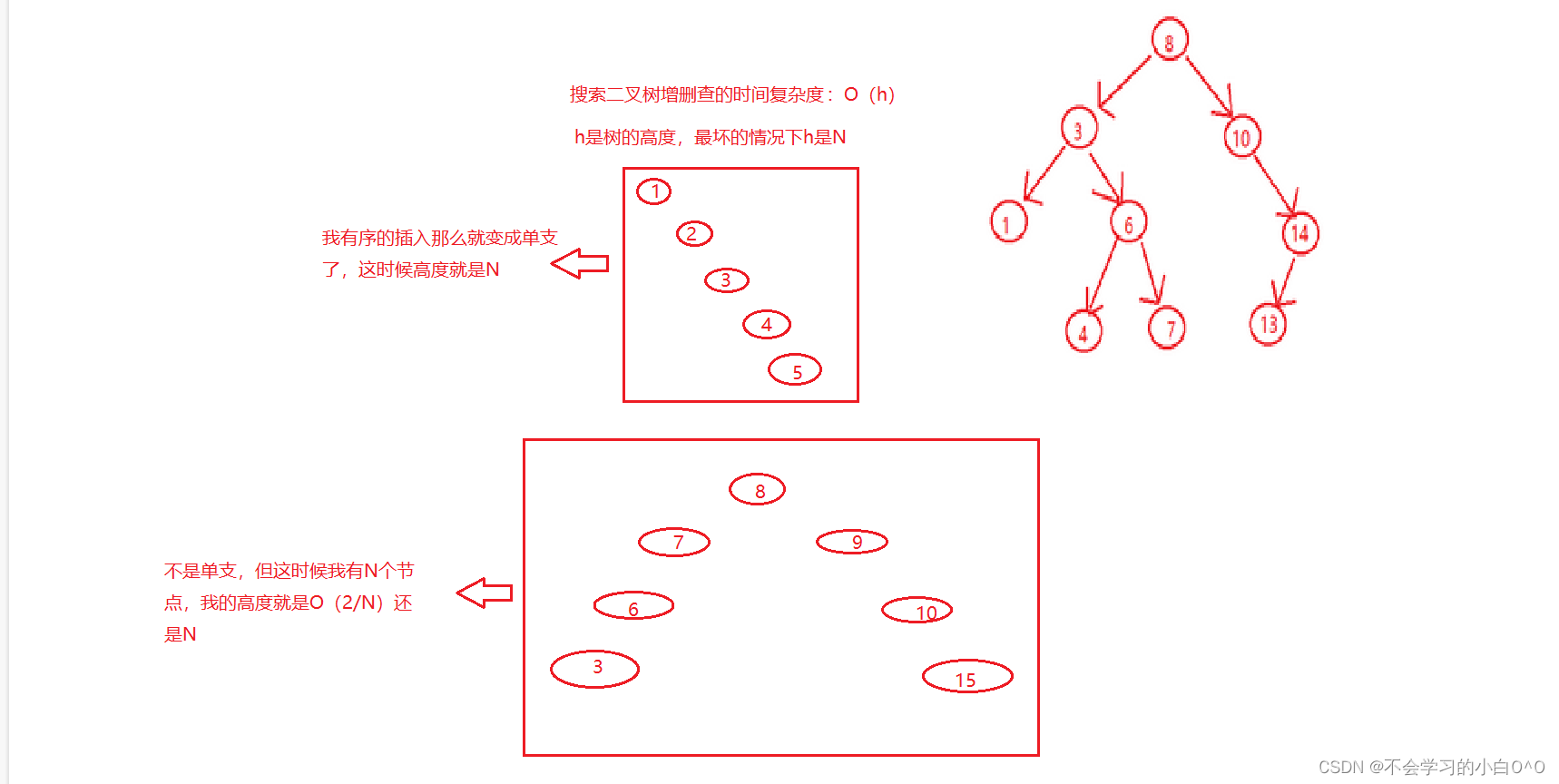
所以搜索二叉树还是有缺陷的
需要被改进---》改进的方案就是平衡树 ----- AVL树、红黑树