title: 卡特兰数 date: 2021-02-28 16:27:10 tags: 算法

概念

卡特兰数 的通项公式为

又根据 组合数的计算公式:

可得:

同时满足递推关系式:

应用

1.括号化问题（或者01的个数问题）

“

矩阵链乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案？(h(n)种)

2.出栈次序问题

“

一个栈(无穷大)的进栈序列为1,2,3,…n,有多少个不同的出栈序列?

与 问题1解法相同, 进栈相当于左括号,出栈相当于右括号

另两个类似例子:

(1)有2n个人排成一行进入剧场（或者商店买东西）。入场费5元。其中只有n个人有一张5元钞票，另外n人只有10元钞票，剧院无其它钞票，问有多少中方法使得只要有10元的人买票，售票处就有5元的钞票找零？(将持5元者到达视作将5元入栈，持10元者到达视作使栈中某5元出栈)

还是与1类似,5块钱相当于左括号,10块钱相当于右括号

(2)在圆上选择2n个点,将这些点成对连接起来，使得所得到的n条线段不相交的方法数。

3.凸多边形问题

（1）一个凸的n边形，用直线连接他的两个顶点使之分成多个三角形，每条直线不能相交，问一共有多少种划分方案。

(2)类似：一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她从不穿越（但可以碰到）从家到办公室的对角线，那　　 么有多少条可能的道路？

(3)类似：在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数? 例如n+2个点的凸多边形，这里n=4，通过卡特兰数的推导可以得出h(4)=14。

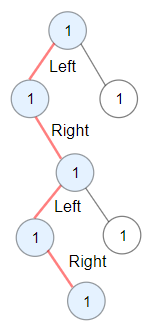
4.给定节点组成二叉树的问题

“

给定N个节点，能构成多少种形状不同的二叉树？

先取一个点作为顶点,然后左边依次可以取0至N-1个,相对应的,右边是N-1到0个,两两配对相乘,就是h(0)*h(n-1) + h(2)*h(n-2) +…+ h(n-1)h(0)=h(n)（能构成h(N)个）

leetcode-96 不同的二叉搜索树

5.n*n棋盘从左下角走到右上角而不穿过主对角线的走法

a.在 nn的格子中，只在下三角行走，每次横或竖走一格，有多少中走法？其实向右走相当于进栈， 向左走相当于出栈，本质就是n个数出栈次序的问题，所以答案就是卡特兰数。（利用这个模型，可以解决这个卡特兰问题的变形问题，并顺便给进出栈问题的解法一个几何解释）

b.有n+1个叶子的满二叉树的个数？事实上，向左记为+1，向右记为−1，按照向左优先的原则，从根节点开始遍历．例如第一个图记为+1,+1,+1,−1,−1,−1,于是由卡特兰数的含义可得满二叉树的个数为Cn。

参考:

卡特兰(Catalan)数概念的简要介绍

史上最详细的卡特兰数浅谈

卡特兰数的证明

LeetCode 96之卡特兰数

卡特兰数/概率/蓄水池抽样