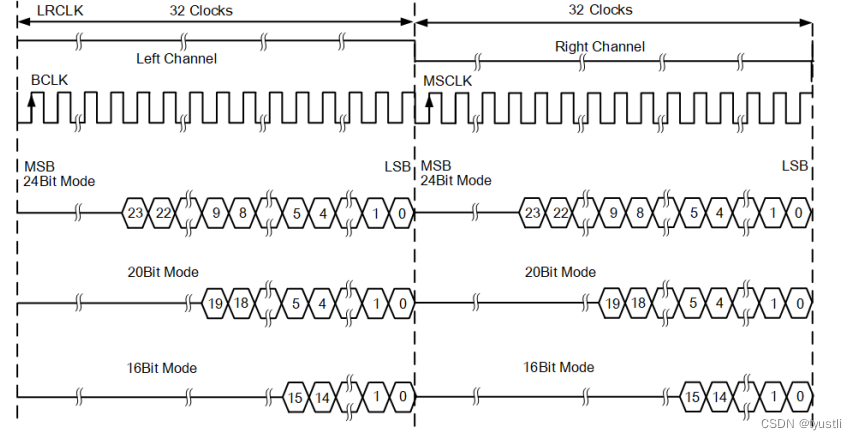
A 判断通过操作能否让字符串相等 I
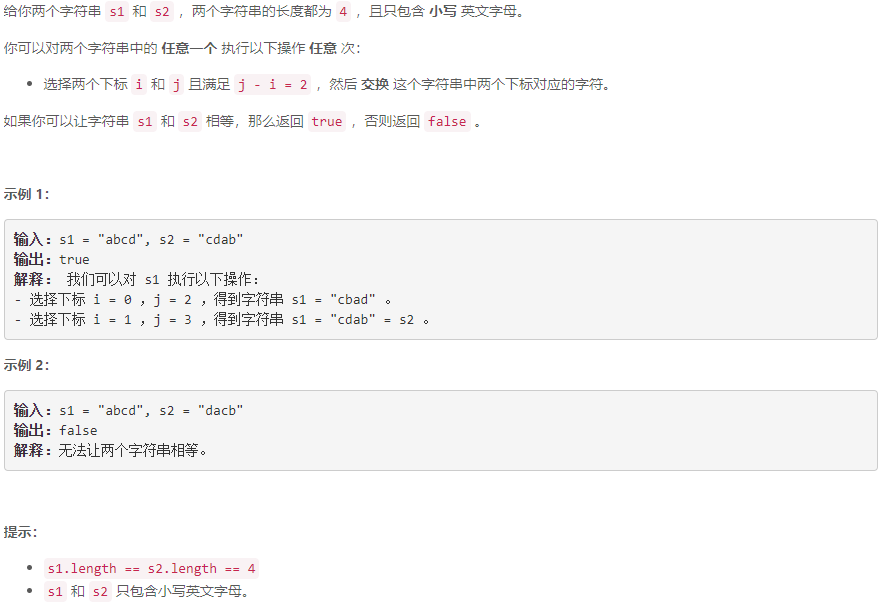
s 1 s1 s1和 s 2 s2 s2第 1 1 1、 2 2 2位若同位置不等,则 s 1 s1 s1交换对应的 i i i和 j j j位置,之后判断 s 1 s1 s1和 s 2 s2 s2是否相当
class Solution {
public:bool canBeEqual(string s1, string s2) {for (int i = 0; i + 2 < 4; i++)if (s1[i] != s2[i])swap(s1[i], s1[i + 2]);return s1 == s2;}
};
B 判断通过操作能否让字符串相等 II
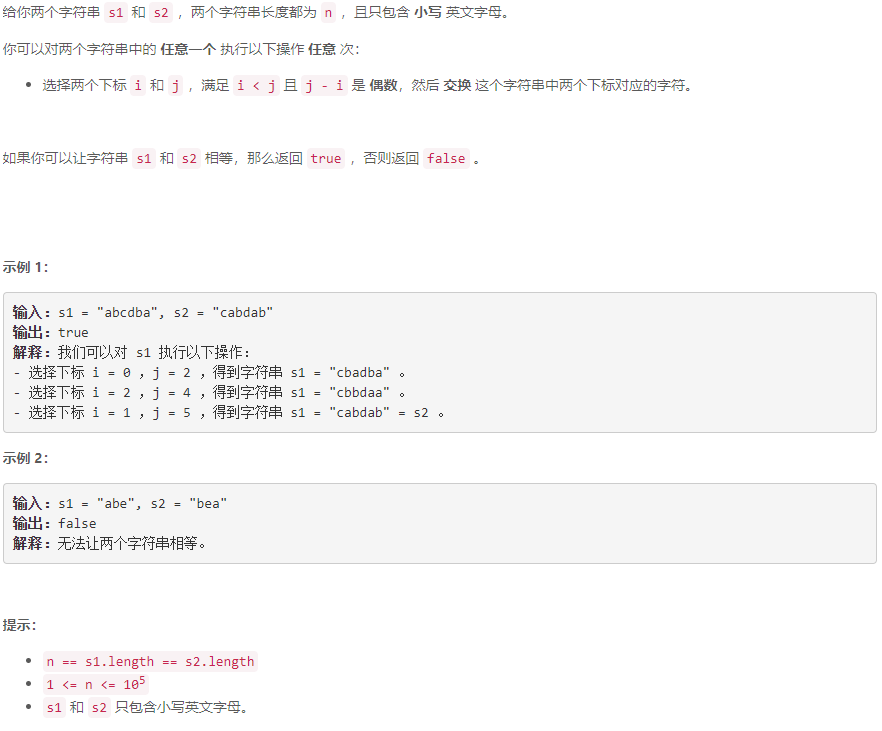
排序:一个字符串中下标奇偶性相同的位置可以任意交换,所以将字符串按下标奇偶划分成两个子串,再对子串分别排序,再分别比较两个串的子串
class Solution {
public:bool checkStrings(string s1, string s2) {string a1, b1, a2, b2;for (int i = 0; i < s1.size(); i++)if (i & 1)a1.push_back(s1[i]);elseb1.push_back(s1[i]);for (int i = 0; i < s2.size(); i++)if (i & 1)a2.push_back(s2[i]);elseb2.push_back(s2[i]);sort(a1.begin(), a1.end());sort(b1.begin(), b1.end());sort(a2.begin(), a2.end());sort(b2.begin(), b2.end());return a1 == a2 && b1 == b2;}
};
C 几乎唯一子数组的最大和
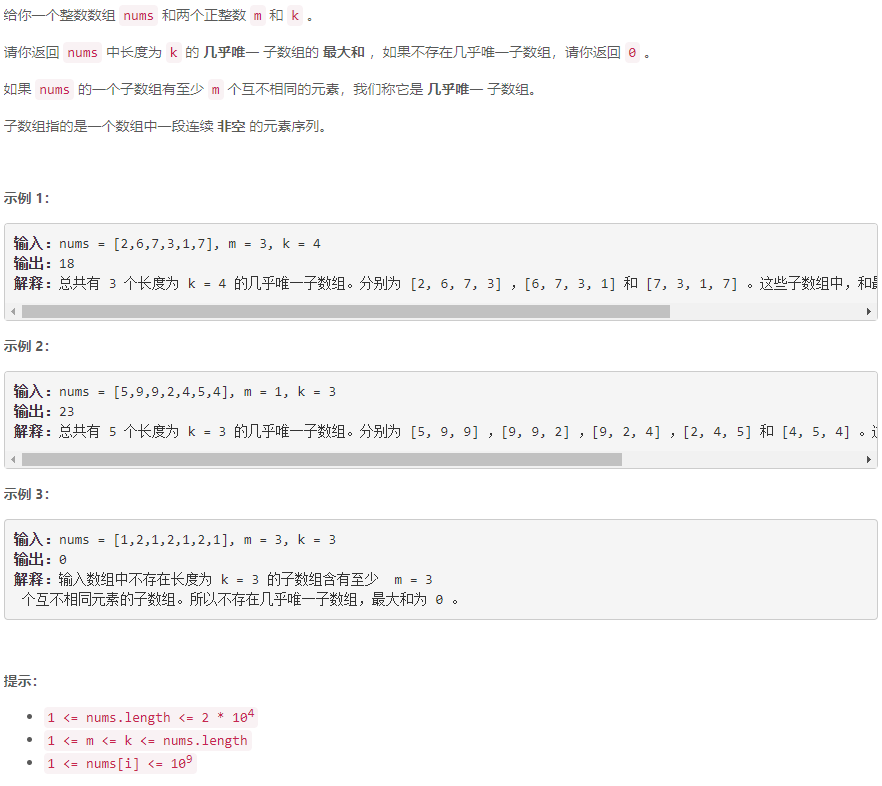
滑动窗口+哈希:用滑动窗口枚举长为 k k k 的子数组,用哈希表记录子数组中各元素出现的次数,以维护当前子数组中不同元素的个数
class Solution {
public:long long maxSum(vector<int> &nums, int m, int k) {unordered_map<int, int> f;//子数组中各元素出现的次数int cnt = 0;//当前子数组中不同元素的个数long long s = 0;//当前子数组元素和for (int i = 0; i < k - 1; i++) {if (++f[nums[i]] == 1)cnt++;s += nums[i];}long long res = 0;for (int l = 0, r = k - 1; r < nums.size(); l++, r++) {//枚举长为k的子数组nums[l,r]if (++f[nums[r]] == 1)cnt++;s += nums[r];if (cnt >= m)res = max(res, s);if (--f[nums[l]] == 0)cnt--;s -= nums[l];}return res;}
};
D 统计一个字符串的 k 子序列美丽值最大的数目
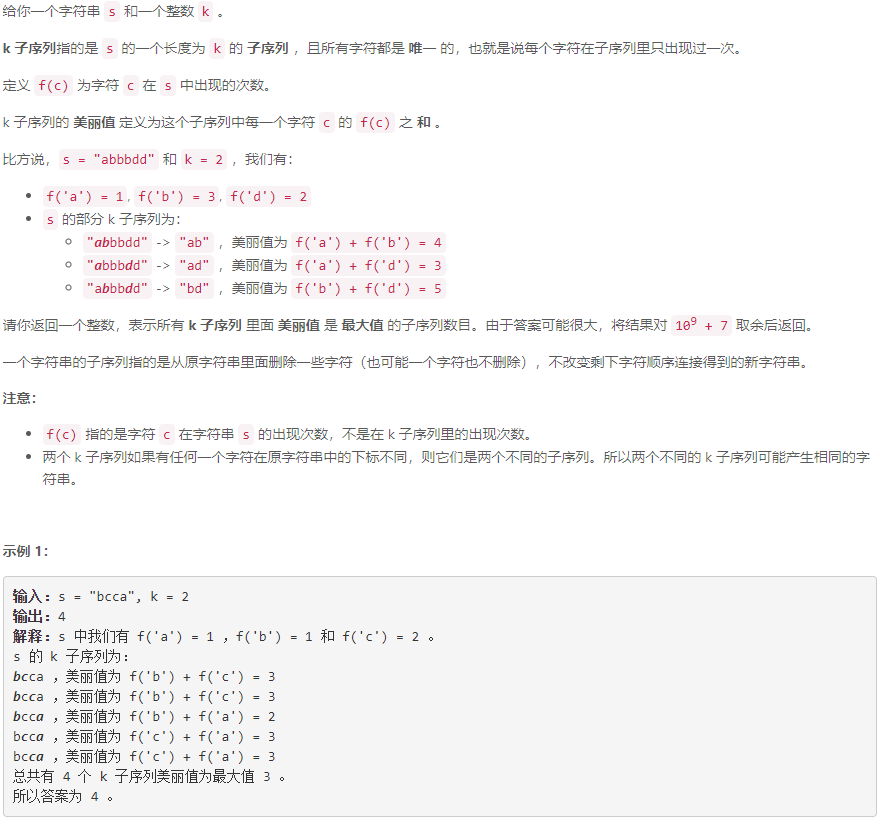
排序+计数:当 k > 26 k>26 k>26 时显然不存在 k k k 子序列,所以答案为0。当 k ≤ 26 k\le 26 k≤26 时,将字符出现次数数组 f f f 降序排序,设排序后的 f f f 中大小关系有: f 0 ≥ ⋯ > f l = ⋯ = f k − 1 = ⋯ = f r > ⋯ f_0\ge\cdots>f_l=\cdots=f_{k-1}=\cdots=f_r>\cdots f0≥⋯>fl=⋯=fk−1=⋯=fr>⋯
则在美丽值最大的 k k k 子序列中,前 l l l 个不同字符是必选的,之后会在 [ l , r ] [l,r] [l,r] 范围内选 k − l k-l k−l 个不同的字符,所以答案即为(注意取模): ( ∏ k = 0 k < l f k ) × ( r − l + 1 k − l ) × ( f k − 1 ) k − l \left ( \prod_{k=0}^{k<l} f_k \right ) \times \binom{r-l+1}{k-l} \times (f_{k-1})^{k-l} (k=0∏k<lfk)×(k−lr−l+1)×(fk−1)k−l
class Solution {
public:using ll = long long;ll mod = 1e9 + 7;ll c[27][27];ll get(int n, int k) {//求组合数: C(n,k)if (c[n][k] != INT64_MIN)return c[n][k];if (k == 0 || n == k)return c[n][k] = 1;return c[n][k] = (get(n - 1, k) + get(n - 1, k - 1)) % mod;}ll fpow(ll x, ll n) {//快速幂: x^nll res = 1;for (ll e = x; n; e = (e * e) % mod, n >>= 1)if (n & 1)res = (res * e) % mod;return res;}int countKSubsequencesWithMaxBeauty(string s, int k) {if (k > 26)return 0;vector<ll> f(26);for (auto &c: s)f[c - 'a']++;sort(f.begin(), f.end(), greater<int>());//降序排序if (f[k - 1] == 0)//不存在k子序列return 0;int r = k - 1;while (r + 1 < 26 && f[r] == f[r + 1])//定位rr++;ll res = 1;int l = 0;for (; f[l] != f[k - 1]; l++)res = (res * f[l]) % mod;for (int i = 0; i <= 26; i++)for (int j = 0; j <= 26; j++)c[i][j] = INT64_MIN;//初始化标志res = (res * fpow(f[k - 1], k - l) % mod * get(r - l + 1, k - l)) % mod;return (res + mod) % mod;}
};