手撕二叉平衡树-编程知识

今天给大家带来的是平衡树的代码实现，如下：

#pragma once 
#include <iostream>
#include <map>
#include <set>
#include <assert.h>
#include <math.h>
using namespace std;
namespace cc
{template<class K, class V>struct AVLnode{int _bf = 0;pair<K, V> _val;AVLnode<K, V>* _left;AVLnode<K, V>* _right;AVLnode<K, V>* _parent;AVLnode(const pair<K, V>& val = pair<K, V>(), AVLnode<K, V>* left = nullptr, AVLnode<K, V>* right = nullptr, AVLnode<K, V>* parent = nullptr): _val(val), _left(left), _right(right), _parent(parent){}};template<class K, class V>class AVL{public:typedef AVLnode<K, V> node;//此parent其实就相当于是旋转点void revolveL(node* parent){//需要改变的节点node* sub = parent->_right;node* subl = sub->_left;//如果根节点是parentif (_root == parent){_root = sub;sub->_parent = nullptr;sub->_left = parent;parent->_parent = sub;parent->_right = subl;if (subl)subl->_parent = parent;}//此旋转点不是根节点else{node* pparent = parent->_parent;if (pparent->_left == parent)pparent->_left = sub;elsepparent->_right = sub;sub->_parent = pparent;sub->_left = parent;parent->_parent = sub;parent->_right = subl;if (subl)subl->_parent = parent;}//旋转完成,更新平衡因子sub->_bf = 0;parent->_bf = 0;}void revolveR(node* parent){node* sub = parent->_left;node* subr = sub->_right;if (_root == parent){_root = sub;sub->_parent = nullptr;sub->_right = parent;parent->_parent = sub;parent->_left = subr;if (subr)subr->_parent = parent;}else{node* pparent = parent->_parent;if (pparent->_left == parent)pparent->_left = sub;elsepparent->_right = sub;sub->_parent = pparent;sub->_right = parent;parent->_parent = sub;parent->_left = subr;if (subr)subr->_parent = parent;}sub->_bf = 0;parent->_bf = 0;}bool insert(const pair<K, V>& x){//根节点为空if (_root == nullptr){_root = new node(x);//节点中父指针已经指向nullptrreturn true;}node* parent = nullptr;node* cur = _root;while (cur){if (x.first < (cur->_val).first){parent = cur;cur = cur->_left;}else if (x.first > (cur->_val).first){parent = cur;cur = cur->_right;}elsereturn false;}cur = new node(x);if ((parent->_val).first > x.first)parent->_left = cur;elseparent->_right = cur;cur->_parent = parent;//插入完成，更新平衡因子while (parent){if (parent->_right == cur)parent->_bf++;else if (parent->_left == cur)parent->_bf--;//此情况说明cur既不是做孩子也不是右孩子，所以直接报错，说明插入的时候出现了问题elseassert(false);if (abs(parent->_bf) == 0)break;else if (abs(parent->_bf) == 1){cur = parent;parent = parent->_parent;}else if (abs(parent->_bf) == 2){//旋转if (parent->_bf == 2 && cur->_bf == 1){revolveL(parent);break;}else if (parent->_bf == -2 && cur->_bf == -1){revolveR(parent);break;}else if (parent->_bf == -2 && cur->_bf == 1){node* sub = parent->_left;node* subr = sub->_right;int bf = subr->_bf;revolveL(sub);revolveR(parent);if (bf == 0){parent->_bf = 0;sub->_bf = 0;subr->_bf = 0;}else if (bf == 1){sub->_bf = -1;parent->_bf = 0;subr->_bf = 0;}else if (bf == -1){sub->_bf = 0;parent->_bf = 1;subr->_bf = 0;}elseassert(false);break;}else if (parent->_bf == 2 && cur->_bf == -1){node* sub = parent->_right;node* subl = sub->_left;int bf = subl->_bf;revolveR(sub);revolveL(parent);subl->_bf = 0;if (bf == 0){// subl->_bf = 0;sub->_bf = 0;parent->_bf = 0;}else if (bf == 1){sub->_bf = 0;// subl->_bf = 0;parent->_bf = -1;}else if (bf == -1){sub->_bf = 1;//subl->_bf = 0;parent->_bf = 0;}elseassert(false);break;}//如果走到这步，说明这棵树的平衡因子有问题elseassert(false);}elseassert(false);}return true;}int high(){return _high(_root);}bool check(){return _check(_root);}private:node* _root = nullptr;bool _check(node* root){if (root == nullptr)return true;int bf = _high(root->_right) - _high(root->_left) ;if (bf != root->_bf){cout << "bf:不一样" << endl;return false;}cout << "bf:" << bf <<" " << "root:" << (root->_val).first << endl;return _check(root->_left) && _check(root->_right);}int _high(node *root){if (root == nullptr)return 0;int left = _high(root->_left);int right = _high(root->_right);if (left > right)return left + 1;elsereturn right + 1;}};
}

这个仅仅是平衡树的插入，其实二叉平衡树的插入并不难，逻辑就是那么几个，但是难得是细节处的实现，尤其是平衡因子更新的那一块，特别的容易弄混人，只要记住四种模型就可以了。两种单旋，两种双旋，还是有点难以理解的，下面一一讲解

1.左单旋

左单旋大概的图示这样子的：

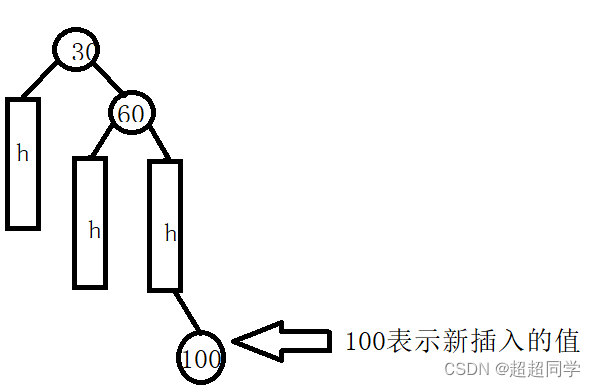
如上图，如果没有插入100，那么此时的二叉平衡树是平衡的，但是此时如果插入100，此时30这个节点的平衡因子是2，所以此时需要旋转来降低这棵树的高度，此时就是左旋。其实此处还分为好几种情况，但是这几种情况都是一样的旋转方法，因为都在60这个节点的右子树中，所以此时就把30当做旋转点，让60左旋，在把60这个节点的左子树链接到30的右指针处就好了。

2.右单旋

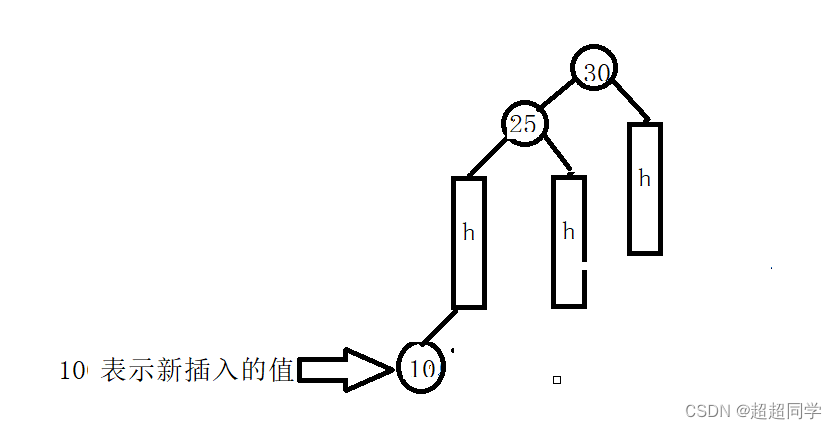
和左单旋一样，因为新插入的节点导致30这个节点的平衡因子为-2，所以此时就要旋转来降低这棵树的高度，此时是要右旋，这个和左旋一样，30是旋转点，25进行右旋，把25这个节点的右子树连接到30这个节点的左子树处就可以了。

3.先左旋，在右旋

这个就是先左旋，在右旋，也是插入了新的节点导致的。这里没有写节点具体的值是因为，因为40这个节点的右子树或是左子树中的值不确定，所以就用了一个空节点来代替插入的值。其实就是两次单旋的结果，先把40以30为旋转点进行左旋，再把60当旋转点进行右旋，此时就旋转完成。而30与40的子树怎么连接参考左单旋与右单旋的旋转方式

4.先右旋，在左旋

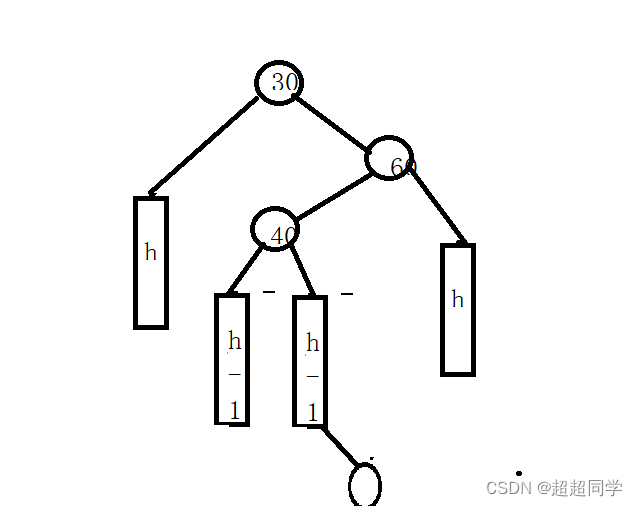
这个模型就是先右旋，在左旋。先把60当旋转点进行旋转，再把30当旋转点进行旋转，至于子树怎么连接，与先左旋，在右旋相同。

以上就是平衡二叉树的旋转方式，下面来总结一下思路：

1.与二叉搜索树的插入一样

2.链接parent指针

3.更新平衡因子

4.如果左右不平衡，那么就开始旋转

增删查时间复杂度：

首先我们知道的是，他是一个二叉树，所以他的高度是log n，而我们在增删查的时候，我们最坏的结果就是要查叶子结点或者所查的节点不在此树，此时它的时间复杂度就是log n，但是他的空间复杂度也是logn,所以个人认为他是以空间换区时间的一种数据结构，但是他的效率确实很高，而对于我们所说的红黑树，其实严格意义来说也是一种logn的算法，但是他没有平衡二叉树这么严谨，平衡二叉树旋转的次数比较多，但是红黑树却没有，旋转其实也是一种消耗，但是旋转的时间复杂度是O(1)，严格来说，有消耗，但是也没那么严重，但是对于红黑树来说，就是尽可能不旋转，减少这种消耗。

对于红黑树的代码以及讲解，下一篇会详细讲解，也会对比AVL树和红黑树的优缺点。期待下一篇内容吧！！谢谢大家支持！！！