目录
1. 概要
2. Gradient Descent
3. Chain rule
3.1 单变量基本链式法则
3.2 单变量全微分链式法则
3.3 小贴士:微分、导数、导函数是什么关系?
4. What and why backpropagation?
5. Backpropagation for a simple neural network
5.1 基于链式法则的表达
5.2 输出层的梯度计算
5.3 隐藏层的梯度计算
5.3.1 f1对w1, b1的梯度
5.3.2 L对f1的梯度
5.3.3 L对w1, b1的梯度
6. Batch Processing
6.1 batch数据集的表示
6.2 forward processing
6.3 backward propagation
附录: Backpropagation History[3]
1. 概要
反向传播是神经网络中常用的一种训练算法,其基本思想是通过计算损失函数对每个权重的梯度,然后使用梯度下降法来优化神经网络的权重。
在神经网络发展的早期,当只有一层网络的时候,梯度下降算法的实现是显而易见的。单层的神经网络(线性回归啊,logistic回归其实都可以看成是单层的神经网络)能做的事情有限。在设计更多层数的神经网络的时候,所遇到的一个根本的难题就是如何(有效地)计算最终的损失函数对除了输出层以外的各层(即隐藏层)的权重参数的梯度。在上世纪八十年代深度学习的先驱们成功地应用反向传播算法解决了这个问题后,深度学习才开始迎来了黄金时代。
本文简单介绍反向传播的技术要点并基于一个简单的三层分类神经网络(输入层、隐藏层、输出层,如下图所示)例子给出具体的数学推导和python实现。
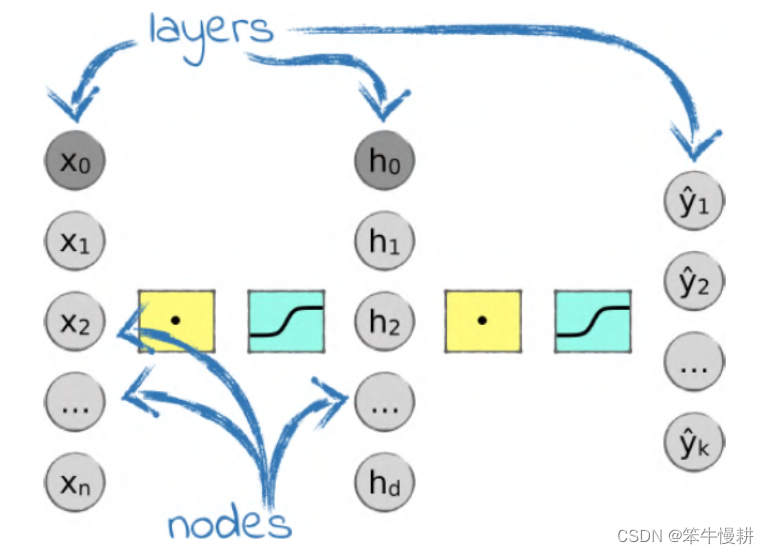
图1 三层分类神经网络(取自[1])
2. Gradient Descent
梯度下降是一种常用的优化算法,用于最小化函数的值。该算法的基本思想是沿着函数在当前点的梯度方向(即函数值变化最快的方向)的相反方向下降,直到到达函数的局部最小值或全局最小值。
梯度下降算法适用于求解具有可导性的函数的最小值,如线性回归、逻辑回归等。它的步骤简单、易于实现,而且可以应用于大量数据的优化问题。
基本的梯度下降算法(vanilla gradient descent)如下所示:
假设有一个函数 ,我们想要找到一个使得
最小的
值即
。梯度下降算法会根据函数的梯度方向来不断更新
的值,直到找到最小值。具体步骤如下:
1. 初始化 的值;
2. 计算函数 的梯度
;
3. 沿着梯度方向更新 的值,即
,其中
称为学习率,控制更新步长的大小;
4. 检查更新后的 值是否满足停止条件,若满足则算法结束,否则回到步骤 2。
通常情况下,梯度下降算法可以分为批量梯度下降(Batch Gradient Descent)、随机梯度下降(Stochastic Gradient Descent)和小批量梯度下降(Mini-Batch Gradient Descent)三种。这些不同的算法采用的更新方式和具体实现方法略有不同,但都遵循了以上基本的梯度下降步骤。
在深度学习中,各路神仙又在基本的梯度下降算法的基础上(vanilla gradient descent)折腾出各种改进变种,比如说,ADAM,ADAGRAD, 等等。万变不离其宗,其中的根本点都是梯度计算以及验梯度反方向进行参数调节。在各种机器学习和深度学习的框架工具中都有这些各种优化算法的实现,因此通常并不需要自己动手去实现梯度下降算法,但是DIY一次对于透彻地理解算法的精髓的确是必需的,正所谓:纸上得来终觉浅绝知此事须躬行。
以上基本算法的描述中考虑的是单变量函数的优化,多变量(多元)函数的优化的道理是相同的。
3. Chain rule
复合函数求导需要用到链式法则,链式法则是backpropagation的核心之一。
以下简单介绍backpropagation所需要的链式法则,包括基本链式法则和最关键的全微分链式法则,详细可以参考[2]。
3.1 单变量基本链式法则
考虑复合函数:,求
令(取中间变量), 这样以上复合函数可以重写成:
这种基本情况下的链式法则为:
(3-1)
以上三种写法等价,但是第一种最为明确,不容易出错。
更深(层级更多的)复合函数的链式法则应用是以上基本情况的自然扩展。比如说,考虑复合函数,y对于x的微分如下所示:
(3-2)
3.2 单变量全微分链式法则
在以上基本情况中,构成复合函数的两层函数都是单变量函数,即y是以u为自变量的单变量函数,u是以x为自变量的单变量函数。其中u是唯一的中间变量。
如果中间变量不是1个,而是有多个呢,比如说:
(3-3)
这种情况下,如何计算y针对于x(考虑x为自变量的话,y是关于x的单变量函数!这里所说的单变量正式指最底层的自变量的个数)的微分呢?这个涉及到多变量微积分中的全微分,故有些作者称为全微分链式法则[2]。
首先,函数y的全微分可以表示如下:
(3-4)
(3-5)
3.3 小贴士:微分、导数、导函数是什么关系?
微分和导数是紧密相关的概念,但并不完全相同。
微分是一种数学运算,它表示函数在某一点处的变化率。具体来说,微分就是指在极限意义下函数值的改变量与自变量值的改变量的比值,即函数在某一点的切线斜率。
而导数是指函数在某一点处的微分值。通过求导可以得到函数在每个点处的导数值,从而得到函数的整体变化趋势和局部特性,如最大值、最小值、拐点等。
因此,微分和导数是密切相关的,但微分是一个概念,而导数是一个具体的数值。
微分和导函数比较接近。两者都是指对函数进行微分运算,不过它们所表示的概念略有不同。微分通常指对函数在某一点上的斜率进行精确计算。在数学上,微分的定义是取极限,并且步骤包括计算函数自变量的微小增量,然后将其带入函数中,计算函数的增量,最后求得极限。微分能够精确地计算函数在某一点的切线斜率,因此在求解极值、曲线的弧长、面积等问题时非常重要。导函数则是指函数在每一点上的导数,即函数的变化率。导函数可以理解为对函数的微分结果,用来表示函数在某一点上的变化率。导函数可以用于判断函数的单调性、拐点、极值等性质。因此,微分和导函数虽然在计算过程和概念上略有不同,但它们都是对函数进行微分运算的概念。
不过,实际工程应用中,一般来说三者就当一回事处理了吧。。。
4. What and why backpropagation?

图2 gradient descent alogorithm concept diagram
图1所示的三层神经网络(关于神经网络的层数,不同的作者可能有不同的看法。有些人把输入层计入层数,有些则不计入。上文中当我们说单层神经网络时其实就不把输入层当作一层计数。这里说三层就是把输入层计入了。有点乱,不过无所谓了。。。你懂就行)的基于梯度下降进行训练优化的计算框图如上图所示。其中S()表示softmax函数。
要进行上图所示的基于梯度下降算法的训练优化,一方面是要计算出损失函数针对每一层的每一个权重参数的梯度‘另一方面就是基于梯度下降算法进行参数微分。很简单。。。嗯,是的,说起来很简单。
理论上来说,基于上一节所介绍的链式法则,在网络结果(相应的,与之对应的计算图:ocomputation graph)确定后可以直接写出损失函数针对每一个权重参数的梯度(偏微分)表达式,然后针对此进行编程实现即可!但是且慢,现代神经网络几十层、上百层的深度,想象一下按照链式法则把梯度表达式写出来看看,尤其是对于靠前面的网络层级(即离损失函数计算最远的那些地方)。。。简而言之,理论上可以计算并不等于具有实现可行性,要具有实现可行性必需能够在保证性能不会受损失的前提条件下简易高效地实现。
这就到了反向传播算法登场亮相的时刻了。只有在反向传播算法解决了高效地实现梯度计算的问题,才使得深度神经网络的实现称为可能(当然还得结合其它很多关键技术)。
反向传播算法的精髓在于,它不是一次性地针对所有各层权重参数计算损失函数关于它们的梯度,而是从输出层以倒序的方式逐层计算。假定输出层为第N层,
首先,计算损失函数针对第N层的权重参数和输入的梯度;
然后,基于损失函数针对第N层的输入的梯度,计算损失函数针对第N-1层的权重参数和输入的梯度;
然后,基于损失函数针对第N-1层的输入的梯度,计算损失函数针对第N-2层的权重参数和输入的梯度;
然后,依此类推,直到计算完第一个隐藏层(输入层之后的第一个有效层)的权重参数的梯度(此时不再需要计算针对第一个隐藏层的输入的梯度)。
以上除了第N层的梯度计算以外,其它各层的梯度计算都涉及到链式法则。
所以,反向传播算法可以看作是链式法则的一种应用,关键在于提升计算效率使其具有实现可行性。由于是从最后一层反向地向前一层一层地计算,将中间梯度计算结果逐层地反向向前面的层传播,故得名反向传播。Backpropagation involves the calculation of the gradient proceeding backwards through thefeedforward network from the last layer through to the first. To calculate the gradient at aparticular layer, the gradients of all following layers are combined via the chain rule of calculus。
反向传播的一个显而易见的好处,它省掉了许多的重复运算。这个在下一章的例子中能更清晰地看出来。
下一章我们将以图2所示简单的三层网络的例子来看看反向传播算法具体是怎么一回事。
5. Backpropagation for a simple neural network
5.1 基于链式法则的表达
首先,把图2所示神经网络的前向计算用以下一组数学公式表达出来:
(5-1)
梯度下降算法需要先求出L针对w1,b1,w2,b2的梯度(这里用偏微分表示梯度),其计算公式如下所示:
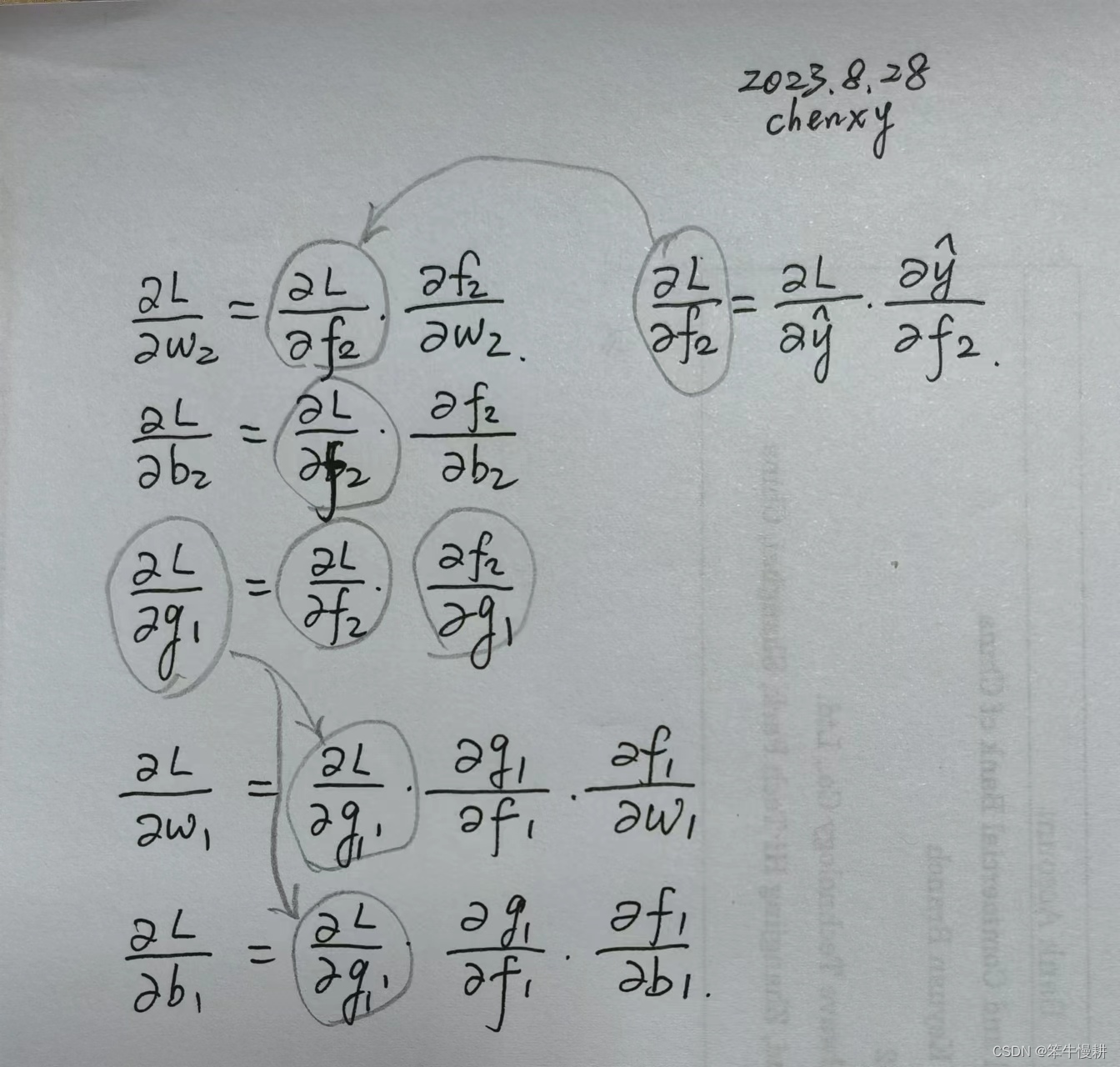
上半截是L针对输出层的权重参数w2,b2及其输入g1 的梯度计算。
下半截是L关于隐藏层的权重参数w1,b1的梯度计算。由于只有两个实质的层,这就是全部了。
L针对g1的梯度在计算w2和b2的梯度时并不需要,但是在计算前一层的w1和b1的梯度(注意,这里为了简介,说“w1的梯度”实际上意思是L针对w1的梯度,余者类推)需要用到L关于g1的梯度。
梯度的(反向)传播就是通过损失函数针对各层的数据输入(或者说上一层的数据输出)的梯度来进行传播的。比如说以上的和
。这样的话,在计算L对w1和b1的梯度时就不必从根子上(比如说
)开始计算。通过这种逐层传递,将长长的梯度计算链条分割成一段段来进行处理,也相当于一种分而治之的策略吧。
本例只有两层的梯度计算,所以看起来逐层传递的价值和必要性并不是那么大(毕竟蛮力计算也是可以的),想象一下几十上百层的网络时就能体会到这种逐层反向传播的优势(甚至说绝对必要性)所在了。
接下来完成这个简单的神经网络的具体梯度计算,并给出这个基于反向传播的梯度计算的python实现。
根据[4]Softmax, Cross-entropy Loss and Gradient derivation and Implementation中的推导我们已经知道(注意,在[4]用表示logits,对应于本文中所述的S()的输入
。注意:
是个向量),在采用softmax activation以及cross-entropy loss的前提条件下有:
(5-2)
5.2 输出层的梯度计算
基于(5-1)和(5-2)接下来求L对w2的梯度表达式。向量/矩阵微积分虽然最后结果写出来非常简洁,但是实际上并不是像单变量微积分那样直观。保险的做法是分解为各分量,通过链式法则计算,然后再拼成向量(或矩阵)表达形式。除非你对向量(矩阵)微积分的运算跟对四则运算那样捻熟于心。具体推导过程如下所示(以下如果没有特别提起,缺省的都是矩阵乘法):

注意,与
的下标关系成转置关系是因为numerator layout的缘故(关于numerator layout vs denominator layout,参见[2])。

(5-3)
同样,可以得到:
(5-4)
为了隐藏层的梯度计算,这里还要计算出L对于输出层的输入的梯度。同样可以得到:
(5-5)
详细推导过程如下所示:
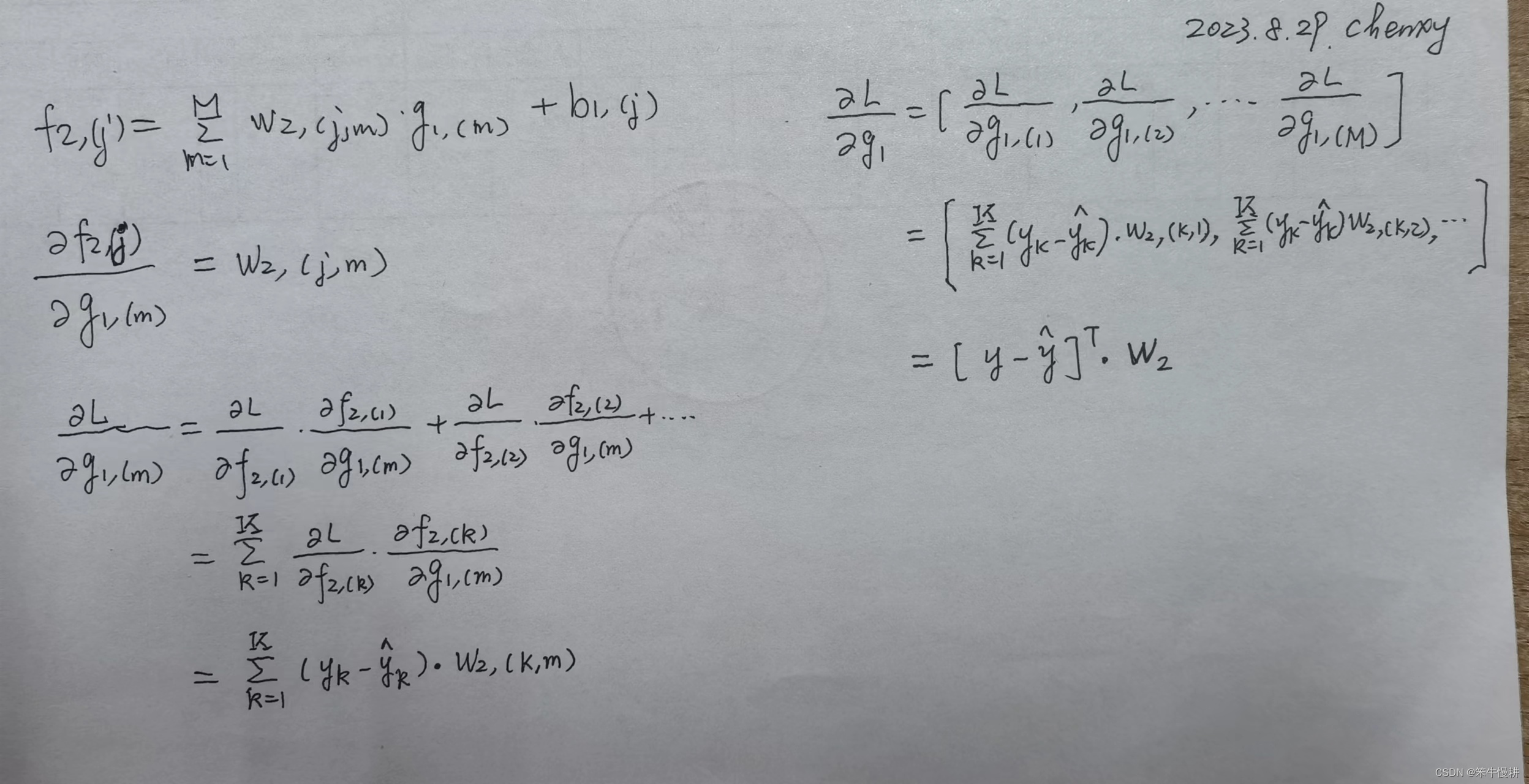
5.3 隐藏层的梯度计算
接下来,要基于计算L对隐藏层的权重参数w1和b1的梯度。
由前文知道,
(5-6)
如前所述,涉及向量和矩阵的微分再加上链式法则并不是非常直观,除非非常熟悉,否则很难直接以向量和矩阵为单位应用链式法则进行演算。但是从L到(w1,b1)的距离很长(想一想,其实才两层网络而已!),像上一节一样分解为标量形式进行处理,然后再组合会向量/矩阵形式已经非常难以处理了。
以下采用分而治之的方式来推导看看。首先考虑对
和
的梯度。
5.3.1 f1对w1, b1的梯度

(5-7)
注意,由于是个向量(1阶张量),而
是个矩阵(2阶张量),所以
对
的梯度是一个shape=[M,N,M]的3阶张量!在纸面上很难写出3阶张量,所以以上只给出了
的某个分量对
的梯度。
接下来我们计算L对的梯度。
5.3.2 L对f1的梯度

(5-8)
5.3.3 L对w1, b1的梯度
有了(5-7),(5-8)是不是直接就可以代入(5-6)求得L对w1, b1的梯度呢?理论上是可以的。首先检查各张量的shape看看是不是符合张量乘法的要求。很容易确认确实是满足要求的。一个非常重要的小技巧是在这种涉及到向量、矩阵、张量的复杂运算中,只要shape匹配,几乎就可以恭喜你大概率是对了(想起一个鸡汤故事,说的是一个老师给一个小孩一张撕烂了的地图,让他重新拼起来。小孩很快就拼完了,大出老师意外。问题原因,说地图的反面是一个人像,按照人像去拼很快就能拼出来了。寓意是人对了世界就对了。套用这句话过来就是,shape匹配了,张量运算就对了)。
如果是进行程序实现,事实上就可以到此为止了。剩下的事情交给计算机去处理就好了。
但是,且慢,是的3阶张量,而
是一个1阶张量,它们乘完后到底会得到什么样的东西(目前只知道会得到一个2阶张量。tips: 一阶张量与其它张量相乘有降后者的阶数降一阶的reduce功效),还能简化吗(好奇心是进步之源)?答案是确实可以。换一种策略进行推导,如下所示:

(5-9)
果然可以!就说漂不漂亮!
当然,L对b1的梯度就很简单了。。。由于b没有与x相乘),所以在每一层中b的梯度都是对应的w的梯度计算式去掉该层的输入数据向量就可以了!
(5-10)
6. Batch Processing
第5章的推导是针对一个数据样本(被视为一个列向量)的,但是在实际机器学习或者深度学习中通常数据是以batch的方式进行处理。所以,为了能够平滑地过度到实际的实现中去,需要将以上推导进行进一步扩展,使得高效得batch processing得以变得可能。
6.1 batch数据集的表示
6.2 forward processing
6.3 backward propagation
欲知后事如何且听下回分解!
附录: Backpropagation History[3]
In 1847, the French mathematician Baron Augustin-Louis Cauchy developed a method of gradient descent for solving simultaneous equations. He was interested in solving astronomic calculations in many variables, and had the idea of taking the derivative of a function and taking small steps to minimize an error term.
Over the following century, gradient descent methods were used across disciplines to solve difficult problems numerically, where an exact algebraic solution would have been impossible or computationally intractable.
In 1970, the Finnish master's student Seppo Linnainmaa described an efficient algorithm for error backpropagation in sparsely connected networks in his master's thesis at the University of Helsinki, although he did not refer to neural networks specifically.
In 1986, the American psychologist David Rumelhart and his colleagues published an influential paper applying Linnainmaa's backpropagation algorithm to multi-layer neural networks. The following years saw several breakthroughs building on the new algorithm, such as Yann LeCun's 1989 paper applying backpropagation in convolutional neural networks for handwritten digit recognition.
In the 1980s, various researchers independently derived backpropagation through time, in order to enable training of recurrent neural networks.
In recent years deep neural networks have become ubiquitous and backpropagation is very important for efficient training. Although the algorithm has been modified to be parallelized and run easily on multiple GPUs, Linnainmaa and Rumelhart's original backpropagation algorithm forms the backbone of all deep learning-based AI today.
Reference:
[1] Paolo Perrotta, Programming Machine Learn: From coding to deep-learning
[2] arVix:1802.0152, The Matrix Calculus You Need For Deep Learning, Terence Parr and Jeremy Howard
[3] https://deepai.org/machine-learning-glossary-and-terms/backpropagation
[4] Softmax, Cross-entropy Loss and Gradient derivation and Implementation




![[C++] STL_list常用接口的模拟实现](https://img-blog.csdnimg.cn/d35e1c90df9d4cd7805b8b3eac1d4fa1.png)