目录

一、选择题

二、编程题

1、倒置字符串

2、排序子序列

3、字符串中找出连续最长的数字串

4、数组中出现次数超过一半的数字

一、选择题

1、

题目解析：

二维数组初始化的一般形式是：

数据类型数组名[常量表达式1][常量表达式2] = {初始化数据};

其中，常量表达式1和常量表达式2分别表示数组的行数和列数，初始化数据用花括号括起来，每一行的数据用逗号分隔，每一行的末尾可以加上分号。如果初始化数据的个数少于数组的元素个数，那么剩余的元素会被自动赋值为0。如果省略常量表达式1，那么编译器会根据初始化数据的个数自动推断出数组的行数。如果省略常量表达式2，那么编译器会报错。故答案为B。

2、

题目解析：（1）使用return语句返回一个包含多个值的结构体或者数组；

（2）使用指针或者引用作为函数的形参，通过修改指针或者引用指向的变量来返回多个值；

（3）使用静态变量或者全局变量来存储多个返回值，然后在主调函数中访问它们。

其中，第一种方法和第二种方法是比较常见和推荐的，因为它们可以保证函数的封装性和可重用性，也可以避免潜在的错误和冲突。第三种方法是不建议使用的，因为它会破坏函数的封装性和可重用性，也会增加程序的复杂度和维护成本。

3、

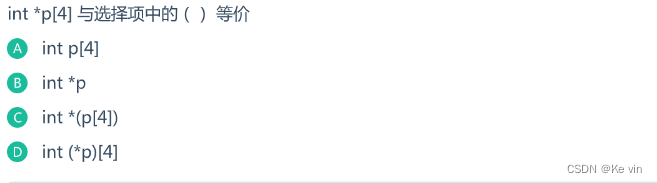
题目解析：int *p[4].是一个指针数组..它表示一个含有4个元素的数组每个元素都是一个指向int类型的指针。由于“[]”的优先级高于“*”，所以p先和“[]”结合，再和“*”结合，所以答案为C。

4、

题目解析：long long类型在32位机器上占用8个字节，也就是64位1；little endian表示低位字节存放在低地址，高位字节存放在高地址。当printf函数打印一个long long类型的变量时，它会把这个变量的8个字节分成两个4字节的部分，然后从低地址处开始读取第一个部分，再读取第二个部分。每个部分都可以看作一个int类型的数。因此，变量a的值为1，在内存中的存储方式为01 00 00 00 00 00 00 00，其中01是低位字节，存放在低地址处。当printf函数打印a时，它会从低地址处开始读取4个字节，也就是01 00 00 00，转换为十进制就是1。注意了，此时a还有4个字节没有被读取，打印b的时候，变量b的值为2，在内存中的存储方式为02 00 00 00 00 00 00 00，其中02是低位字节，存放在低地址处。当printf函数打印b时，它会从低地址处开始读取4个字节，也就是02 00 00 00，但是因为前面的4个字节，所以02变成了第五个字节，所以打印出来是0。变量c的值为3，在内存中的存储方式为03 00 00 00 00 00 00 00，其中03是低位字节，存放在低地址处。当printf函数打印c时，它会从低地址处开始读取4个字节，也就是03 00 00 00，转换为十进制就是2。这是因为03是第9个字节，而不是第一个字节，所以它的权值为2。

二、编程题

1、倒置字符串

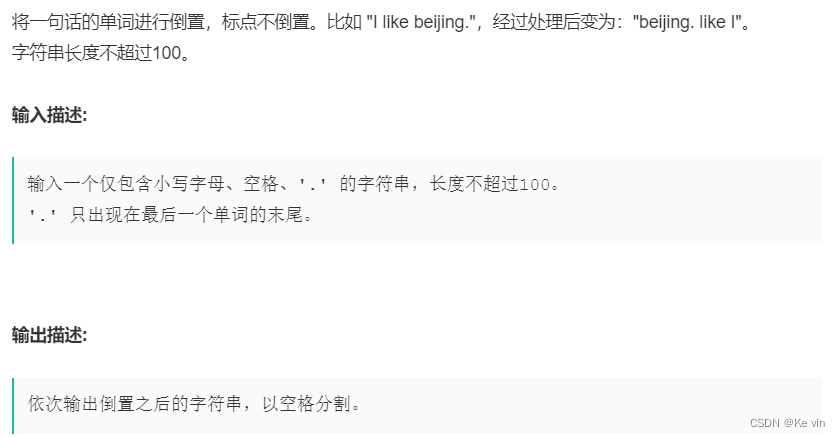
分析题目：先将整个字符串逆置过来，再遍历字符串，找出每个单词，对单词逆置。这里我们使用了stl算法中的reverse，所以这里使用迭代器遍历string。

代码如下：

#include <iostream>
#include<string>
#include<algorithm>
using namespace std;int main() {string str;while (getline(cin, str)) {reverse(str.begin(), str.end()); //整体逆置auto start = str.begin();while (start != str.end()) {auto end = start;while (*end != ' ' && *end != '\0') {end++;}reverse(start, end);if (end != str.end())start = end + 1;elsestart = end;}cout << str << endl;}}

知识点：begin()函数返回一个迭代器，指向字符串的第一个元素。例如，如果有一个字符串string str= "He11o";，那么str.begin()就指向'H’这个字符。end()函数返回一个迭代器，指向字符串的末尾(最后一个字符的下一个位置)。例如，如果有一个字符串string str = "Hello";，那么str.end()就指向'\0’这个空字符，它是字符串的结束标志。这两个函数的范围是左闭右开的，也就是说，它们包含了字符串的第一个元素，但不包含最后一个元素。

reverse 函数的范围是左闭右开的，也就是说，它包含了start指向的元素，但不包含指向end的元素。这个范围可以用中括号表示为[start，end)。例如，如果有一个数组int arr [] = (1，2，3,4，5};，那么reverse (arr + 1， arr + 4);就会翻转数组索引[1，4)的区域，也就是2，3，4这三个元素，翻转后的数组变为{1，4，3，2，5}。

2、排序子序列

题目分析：非递减就是a[i]<=a[i+1]，递减就是a[i]>a[i+1]，非递增就是a[i]>=a[i+1]，递增就是a[i]<a[i+1]。

首先，我们需要定义一个flag变量，用来记录当前的排序状态，初始值为0。如果flag为0，表示还没有确定排序状态；如果flag为1，表示当前是非递减排序；如果flag为-1，表示当前是非递增排序。
然后，我们遍历数组A，比较相邻的两个元素的大小关系。如果A[i] < A[i+1]，表示当前是升序；如果A[i] > A[i+1]，表示当前是降序；如果A[i] == A[i+1]，表示当前没有变化。
接下来，我们根据flag的值和当前的大小关系来判断是否需要分割子序列。如果flag为0，表示还没有确定排序状态，那么我们就根据当前的大小关系来更新flag的值，并且不需要分割子序列。如果flag为1，表示当前是非递减排序，那么我们就判断当前是否是降序，如果是降序，那么我们就需要分割子序列，并且把flag的值更新为-1；如果不是降序，那么我们就不需要分割子序列。如果flag为-1，表示当前是非递增排序，那么我们就判断当前是否是升序，如果是升序，那么我们就需要分割子序列，并且把flag的值更新为1；如果不是升序，那么我们就不需要分割子序列。
最后，我们统计分割出来的子序列的个数，就是最少可以把数组A分为几段排序子序列的答案
代码如下：

#include <iostream>
#include<vector>
using namespace std;int main() {int n = 0;while (cin >> n) {vector<int> list;int count = 1;int flag = 0;list.resize(n);for (int i = 0; i < n; i++) {cin >> list[i];}for (int i = 0; i < n - 1; i++) {if (flag == 0) {if (list[i] == list[i + 1])continue;else if (list[i] < list[i + 1])flag = 1;else flag = -1;} else if (flag == 1) {if (list[i] > list[i + 1]) {count++;flag = 0;}} else {if (list[i] < list[i + 1]){count++;flag = 0;}}}cout << count << endl;}
}

3、字符串中找出连续最长的数字串

题目分析：遍历字符串，使用cur去记录连续的数字串，如果遇到不是数字字符，则表示一个连续的数字串结束了，则将数字串跟之前的数字串比较，如果更长，则更新更长的数字串更新到res。

#include <iostream>
#include<string>
#include<algorithm>using namespace std;int main() {string str, res, cur;cin>>str;for (int i = 0; i < str.length()+1; i++) {if (str[i] >= '0' && str[i] <= '9') {cur += str[i];} else {// 找出更长的字符串，则更新字符串if (res.size() < cur.size())res = cur;elsecur.clear();}}cout<<res;}

4、数组中出现次数超过一半的数字

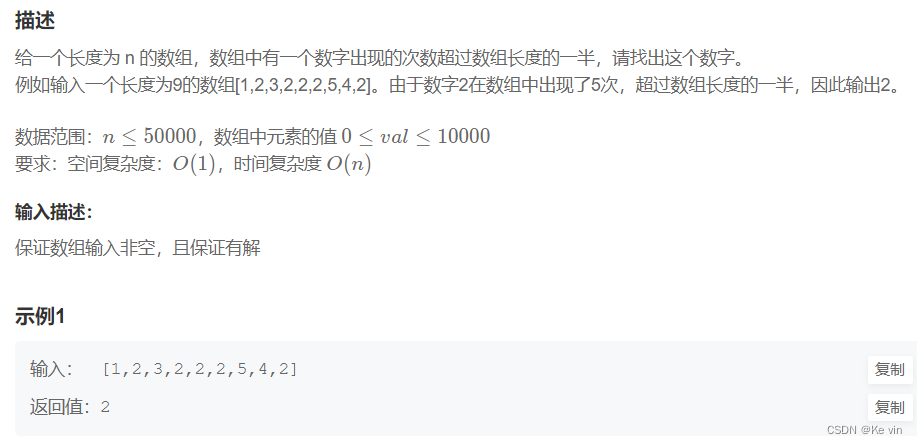
题目分析：

思路一：数组排序后，如果符合条件的数存在，则一定是数组中间那个数。这种方法虽然容易理解，但由于涉及到快排sort，其时间复杂度为O(NlogN)并非最优；

lass Solution {public:int MoreThanHalfNum_Solution(vector<int>& numbers) {sort(numbers.begin(), numbers.end());int middle = numbers[numbers.size() / 2];int count = 0; // 出现次数for (int i = 0; i < numbers.size(); ++i) {if (numbers[i] == middle) ++count;}return (count > numbers.size() / 2) ? middle : 0;}
};

思路二：就是出现次数超过数组长度一半的那个数字
如果两个数不相等，就消去这两个数，最坏情况下，每次消去一个众数和一个非众数，那么如果存在众数，最后留下的数肯定是众数。

class Solution {public:int MoreThanHalfNum_Solution(vector<int>& numbers) {int times=1;int result=numbers[0];for(int i=1;i<numbers.size();i++){if(numbers[i]!=result){if(times==0){result=numbers[i];}else{times--;}   }else {times++;result=numbers[i];}}
return result;}
};