一、常用的搜索逻辑
1、暴力搜索 O(N)
2、二分搜索
前提是有序,可以先用O(NlogN)排序一次,后续每次查找都是logN。
缺点:快排需要容器有随机访问功能,即为顺序表等。
如果不仅要搜索,还要插入删除,此时挪动数据为0(N)
3、二叉搜索树
搜索、插入、删除均为logN
缺点:极端情况下退化为类似链表,变为O(N)
4、二叉平衡搜索树(AVL、RBT)
logN
5、多叉平衡搜索树(B树)
6、哈希表(Hash)
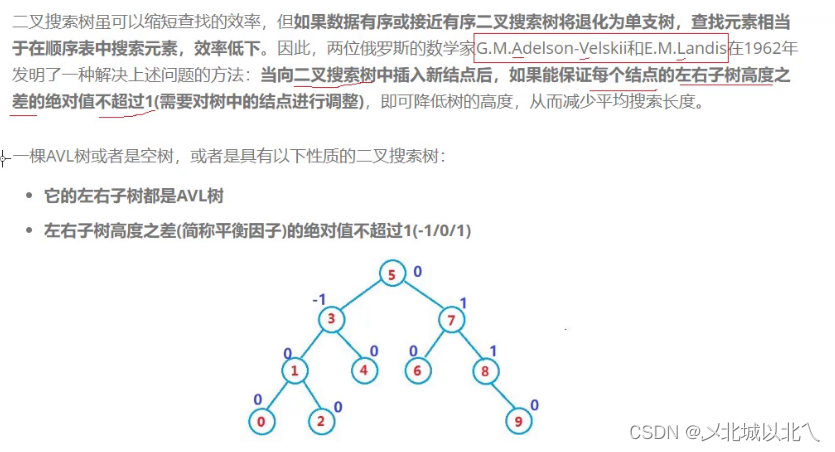
二、AVL树(高度平衡二叉搜索树)
平衡因子版本:bf = H(Right) - H(Left)
正常情况下,bf的取值为 -1 0 1
bf 为0时,为满二叉树 N = 2^h-1个
三、Insert/更新平衡因子
1、作为搜索树的Insert部分
结点的定义:

先找到要插入的位置
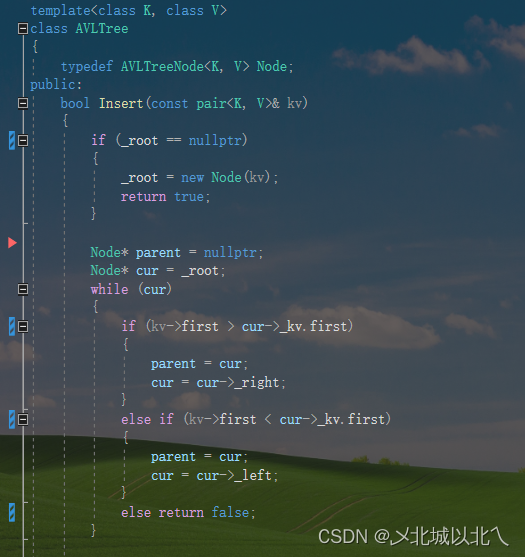
插入在左子树还是右子树

三叉链要记得更新_parent指针
2、更新平衡因子

或者parent更新到nullptr也结束。
四、旋转

旋转完,parent->_bf变为0,即停止更新,break即可。
插入新节点,会一路更新平衡因子,最后只需更新parent->_bf = cur->_bf =0。
1、RotateL
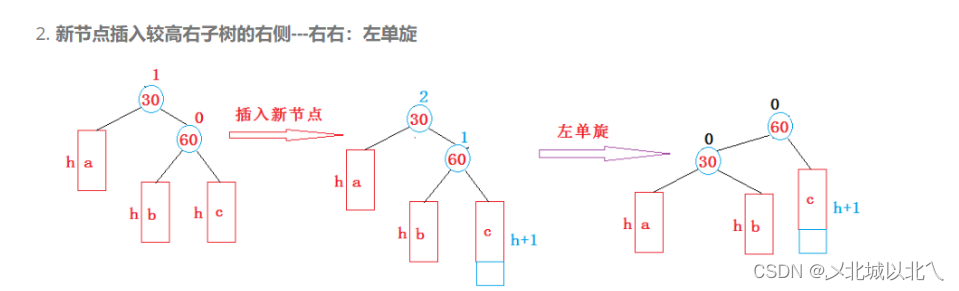
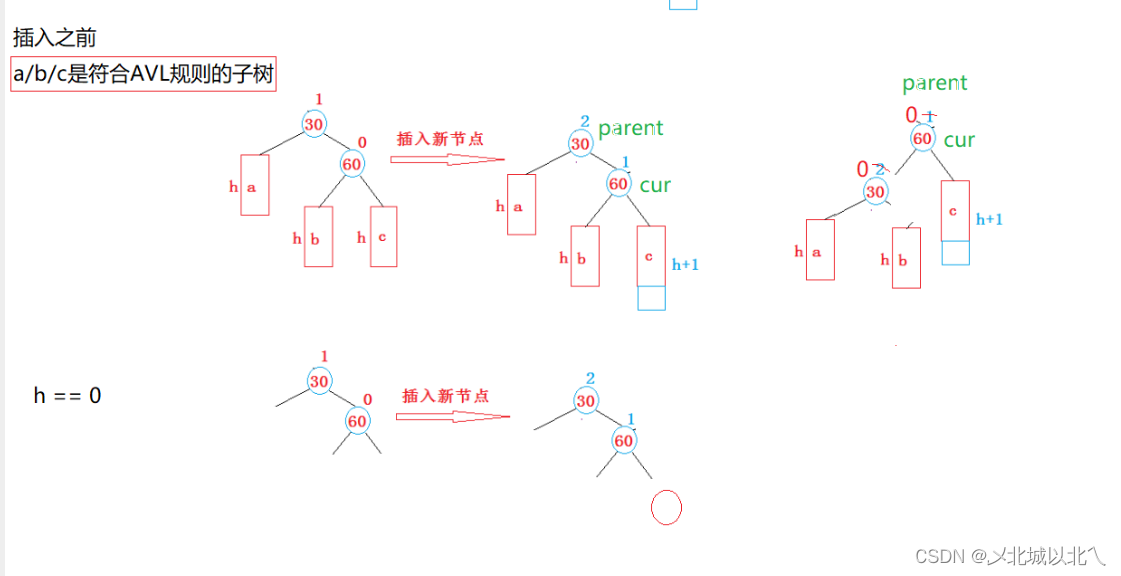
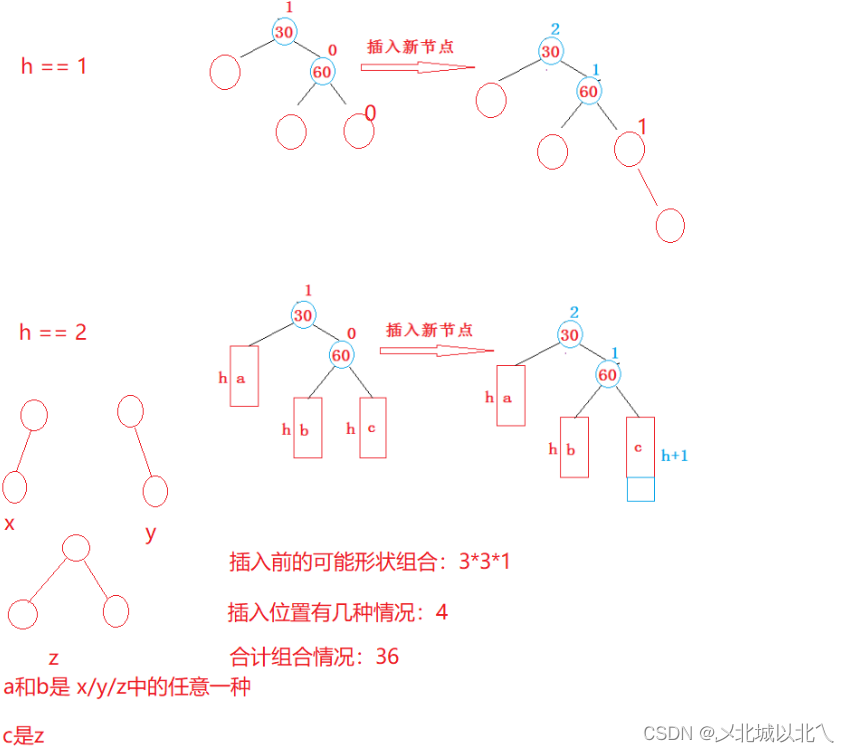
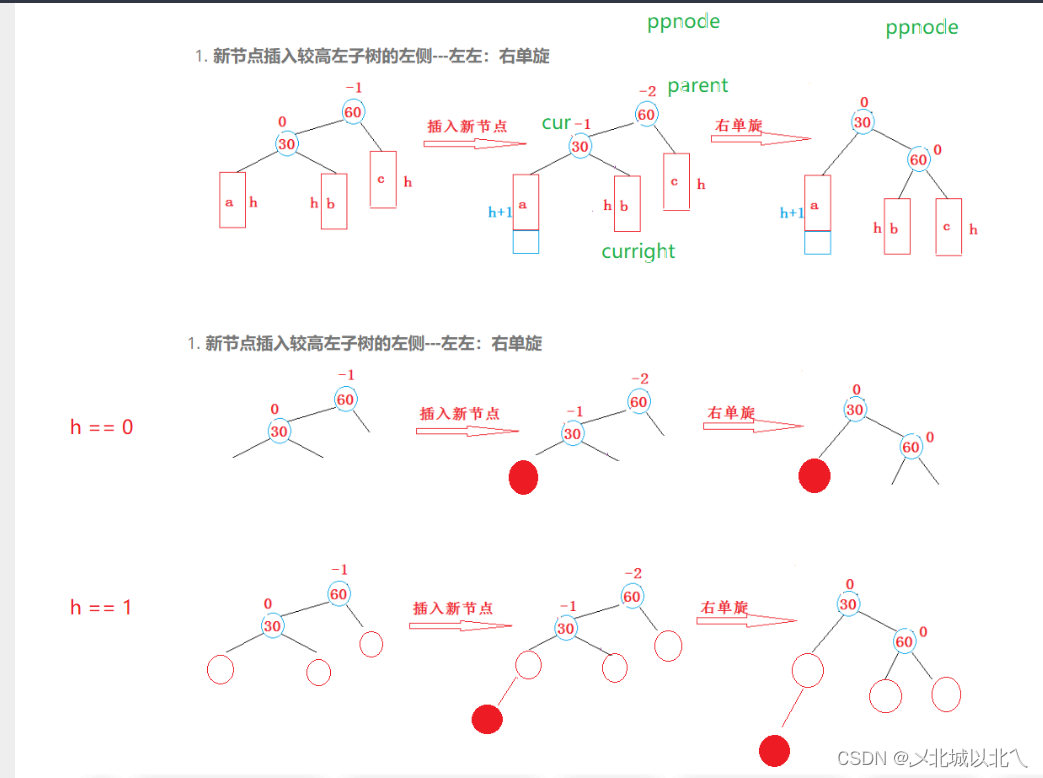
c只能是z,否则会提前停止更新 c所在子树的bf为0
或提前旋转:c所在子树bf为+-2
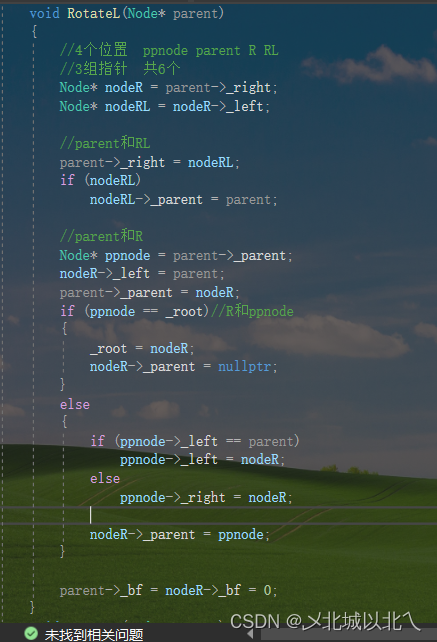
中间判断的是parent是否为root或者ppnode是否为nullptr
2、RotateR

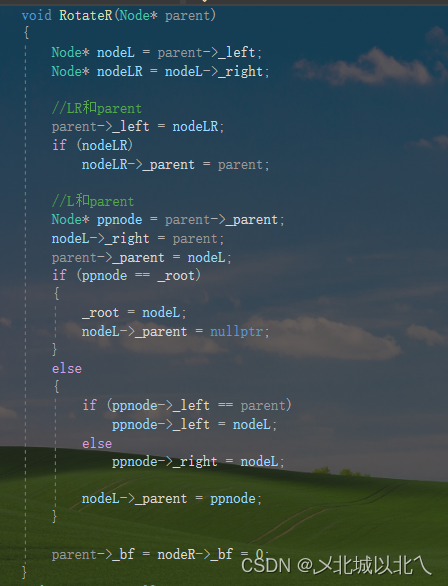
中间判断的是parent是否为root或者ppnode是否为nullptr
3、RotateRL
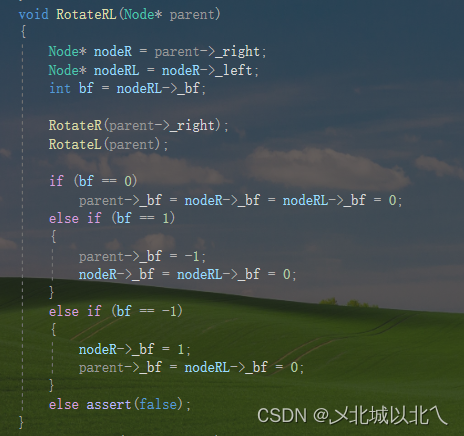
先对 nodeR右旋,然后对parent左旋
最后根据RL的_bf调整平衡因子
4、RotateLR
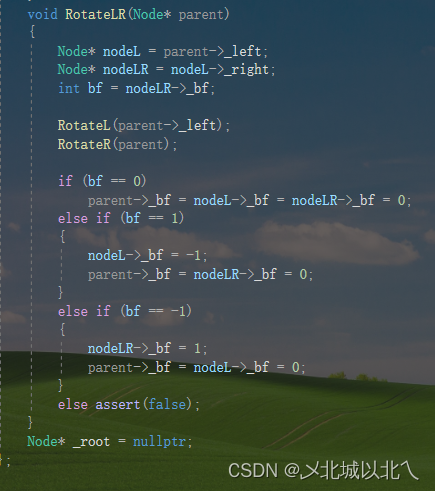
先对L左旋,然后对parent右旋
最后根据LR的_bf调整平衡因子