欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

题目大意

http://acm.hdu.edu.cn/showproblem.php?pid=4773

给定2个不相交的圆以及圆外1点P。求过P并且与另两个圆相切（外切）的圆，这种圆有可能有多个。

基本思路

圆的反演有如下性质：

圆C的圆心为O，则如果有一个圆过点O，则该圆对C的反演是一条直线。反之直线可以反演成圆。
如果两个圆相切，则反演后的几何形状还是相切。

题目要求的是过点P的圆，可以把圆先以P为圆心（半径取1即可）进行反演，然后求公切线，再将切线反演成圆，判断是否外切。

内公切线反演后必有1个圆是内切

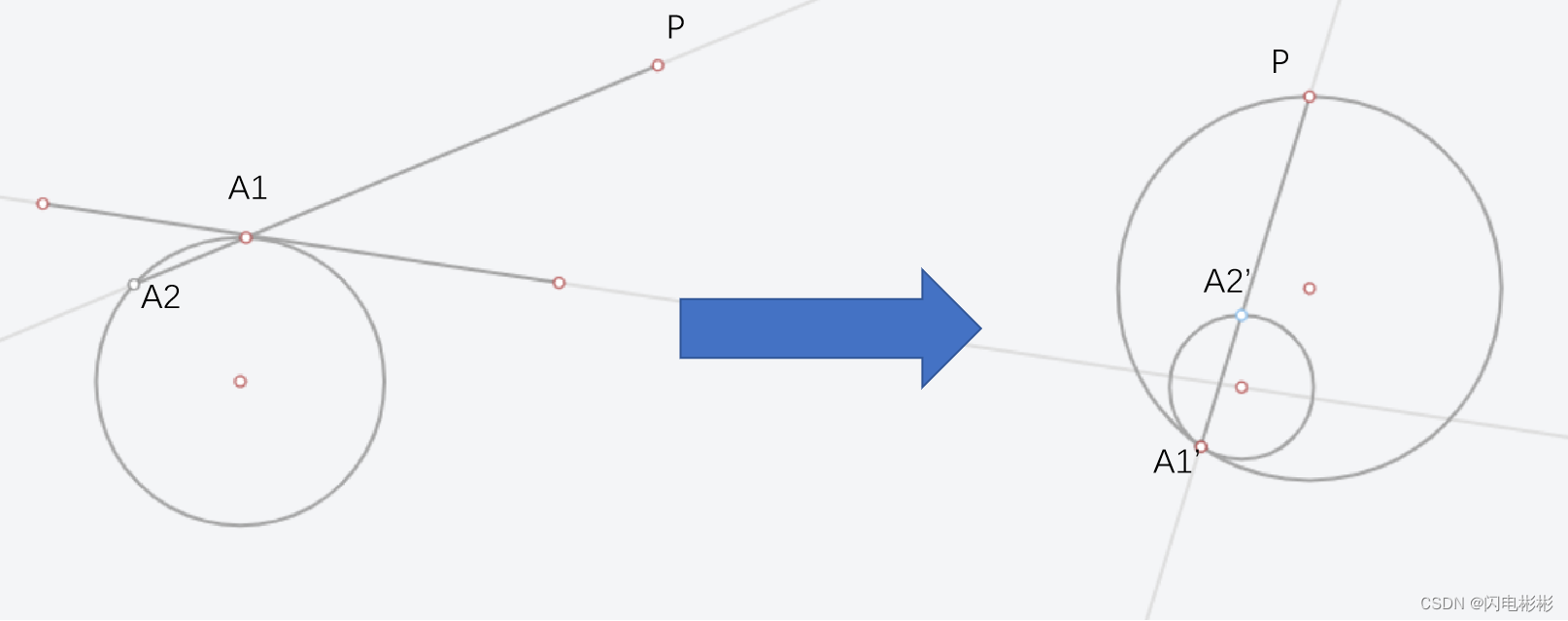
在这里插入图片描述
反演可以理解为一种凸镜反射，反射的特点就是位置会相反，远近会颠倒。
从上图可以看出，当圆处于公切线与P的另一边时，最终结果是内切。
两个圆的内部公切线必有1个圆是处于这种情况。所以只要求外公切线即可。

求解外公切线

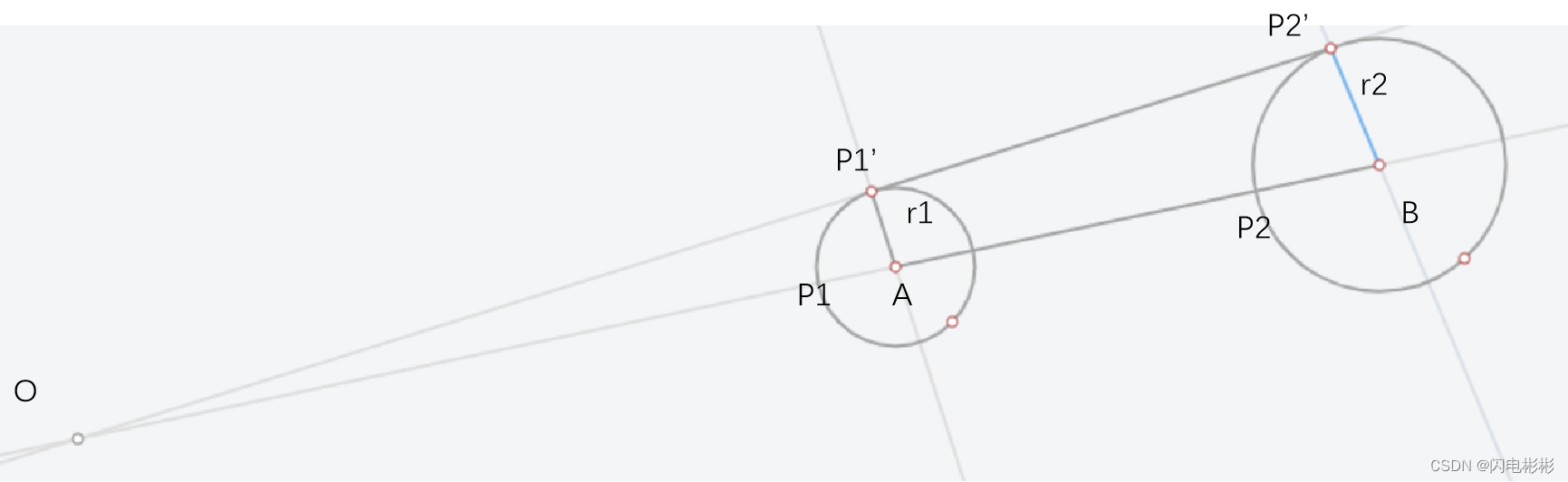
在这里插入图片描述

根据圆的公切线性质可知，
$\angle P1AP1'=\angle P2BP2'，设置值为\alpha$

$\therefore \triangle OAP1' \sim \triangle OBP2', 相似比是\frac {r_1}{r_2}$

P1’, P2’ 可以用P1， P2经过一个旋转得到。

$\begin {bmatrix} cos\alpha&-sin\alpha\\sin\alpha&cos\alpha \end {bmatrix}\cdot (P1-A)+A$

$\begin {bmatrix} cos\alpha&-sin\alpha\\sin\alpha&cos\alpha \end {bmatrix}\cdot (P2-B)+B$

另一边的公切线，相当于是逆时针旋转

$\begin {bmatrix} cos\alpha&sin\alpha\\-sin\alpha&cos\alpha \end {bmatrix}\cdot (P1-A)+A$

$\begin {bmatrix} cos\alpha&sin\alpha\\-sin\alpha&cos\alpha \end {bmatrix}\cdot (P2-B)+B$

通过相似三角形可以解出OA

$cos\alpha =\frac {r_1}{OA}, sin\alpha = \sqrt{1-sin^2\alpha}$

代码实现

#include<stdio.h>
#include<cmath>
#include <algorithm>
#include <vector>using namespace std;class Point {
public:double x, y;Point() {}Point(double a, double b) :x(a), y(b) {}Point(const Point &p) :x(p.x), y(p.y) {}void in() {scanf(" %lf %lf", &x, &y);}void out() {printf("%f %f\n", x, y);}double dis() {return sqrt(x * x + y * y);}Point operator -(const Point& p) const {return Point(x-p.x, y-p.y);}Point operator +(const Point& p) const {return Point(x + p.x, y + p.y);}Point operator *(double d)const {return Point(x *d, y *d);}Point operator /(double d)const {return Point(x / d, y / d);}void operator -=(Point& p) {x -= p.x;y -= p.y;}void operator +=(Point& p) {x += p.x;y += p.y;}void operator *=(double d) {x *= d;y *= d;}void operator /=(double d) {this ->operator*= (1 / d);}
};class Line {
public:Point front, tail;Line() {}Line(Point a, Point b) :front(a), tail(b) {}
};// https://oi-wiki.org//geometry/inverse/#%E5%8F%82%E8%80%83%E8%B5%84%E6%96%99%E4%B8%8E%E6%8B%93%E5%B1%95%E9%98%85%E8%AF%BB
// 根据官方定义实现圆的反演
class Circle
{
public:Point center;double r;Circle(const Point &c, double a):center(c), r(a){}Circle() {}void in() {center.in();scanf("%lf", &r);}void out() {center.out();printf("%f\n", r);}// 不过圆心的圆进行反演，得到1个圆Circle invert(const Circle& A) {Circle B;double oa = (center - A.center).dis();B.r = r * r / 2 * (1.0 / (oa - A.r) - 1.0 / (oa + A.r));double ob = r * r / (oa + A.r) + B.r;B.center = center +  (A.center - center)* ob / oa;return B;}// 过圆心的圆进行反演，得到1条直线Point invert2line(const Circle& c) {return Point();}// 直线反演，得到圆Circle invert2circle(const Line& l) {Point dir = l.front - l.tail;dir /= dir.dis();Circle c(Point(0, 0), 0);// 计算投影Point cdir = center - l.tail;Point project =l.tail + dir*(dir.x * cdir.x + dir.y*cdir.y);// 点乘得到投影长度// 计算圆到直线的距离Point op = project - center;if (op.dis() < 1e-6)return c;// 直线与圆心重合非法// 求解圆上的最远点double d = r * r / op.dis();Point pf = center + op / op.dis() * d;c.center = (center + pf) / 2;c.r = d / 2;return c;}};// 根据相似三角形求解圆的同侧公切线
vector<Line> getTangentLine(const Circle &c1, const Circle &c2) {if (c1.r > c2.r)return getTangentLine(c2, c1);double costheta = 0, sintheta = 1;	// 两圆半径不同，公切线与圆心连线有交点，用相似三角形求解if (c2.r - c1.r > 1e-6) {double oa = (c1.center - c2.center).dis() / (c2.r / c1.r - 1);costheta = c1.r / oa;sintheta = sqrt(1 - costheta * costheta);}// 两个圆上与圆心边线的交点Point pa, pb;Point ab = (c1.center - c2.center);ab /= ab.dis();// 通过两边旋转求解两条公切线vector<Line> res;for (int i = 0; i < 2; i++, sintheta *= -1) {pa = ab;Point pap, pbp;pap.x = costheta * pa.x - sintheta * pa.y;pap.y = sintheta * pa.x + costheta * pa.y;pap = pap * c1.r;pap = pap + c1.center;pb = ab;pbp.x = costheta * pb.x - sintheta * pb.y;pbp.y = sintheta * pb.x + costheta * pb.y;pbp = pbp * c2.r;pbp = pbp + c2.center;res.push_back({pap, pbp});}return res;
}void solve() {Point P, Q, P1, Q1, M;int T;Circle c1, c2,c1invert, c2invert, OC;OC.r = 1;int x1, y1, r1, x2, y2, r2, x3, y3;scanf("%d", &T);while (T--) {scanf("%d %d %d %d %d %d %d %d", &x1, &y1, &r1, &x2, &y2, &r2, &x3, &y3);c1 = Circle(Point(x1, y1),r1);c2 = Circle(Point(x2, y2),r2);OC.center = Point(x3, y3);c1invert = OC.invert(c1);c2invert = OC.invert(c2);auto lines = getTangentLine(c1invert, c2invert);// 对直线进行反演回来，并判断是否与另两圆外切vector<Circle> circles;for (auto &l : lines) {Circle c = OC.invert2circle(l);if (c.r < 1e-6)continue; // 无法得到圆// 判断是否外切//printf("%.6f %.6f\n", (c1.center - c.center).dis(), c1.r+c.r);//printf("%.6f %.6f\n", (c2.center - c.center).dis(), c2.r+c.r);if (abs((c1.center - c.center).dis() - c1.r - c.r)>1e-6)continue;if (abs((c2.center - c.center).dis() - c2.r - c.r)>1e-6)continue;circles.push_back(c);}printf("%d\n", circles.size());for (auto &c : circles) {printf("%.6f %.6f %.6f\n", c.center.x, c.center.y, c.r);}}
}int main() {solve();return 0;
}/*
1
12 10 1 8 10 1 10 101 1 1 10 10 2 3 3
1 1 1 10 10 2 3 10
1 1 1 10 10 2 10 3
12 10 1 8 10 1 10 11
1 1 1 10 10 2 16 100
*/