下载地址:高比例清洁能源接入下计及需求响应的配电网重构
1主要内容
该程序复现《高比例清洁能源接入下计及需求响应的配电网重构》,以考虑网损成本、弃风弃光成本和开关操作惩罚成本的综合成本最小为目标,针对配电网重构模型的非凸性,引入中间变量并对其进行二阶锥松弛,构建混合整数凸规划模型,采用改进的 IEEE33 节点配电网进行算例仿真,分析了需求响应措施和清洁能源渗透率对配电网重构结果的影响。该程序复现效果和出图较好(详见程序结果部分),注释清楚,方便学习!
注意:该程序运行环境为matlab+mosek,需要各位同学下载并安装mosek求解器,通过官网可以申请学术许可,可免费使用365天。
-
目标函数
目标函数为配电网综合运行成本最小,其中考虑了网损成本、弃风弃光成本以及分段开关操作惩罚成本。
-
重要约束条件
常规的功率平衡、节点电压电流等约束不再赘述,重点分析一下网络结构约束和需求响应约束。
网络结构约束:
配电网在重构过程中需满足连通性约束与辐射状约束,具体模型为:
该网络结构约束是采用虚拟潮流方式,之前有几个重构代码也是采用虚拟潮流形式,参考的是《A New Model for Resilient Distribution Systems by Microgrids Formation》,具体模型如下:
仔细观察不难发现,上面的模型是下面的简洁版,在不考虑分布式电源节点对网络切割情况下,两者是等价的。
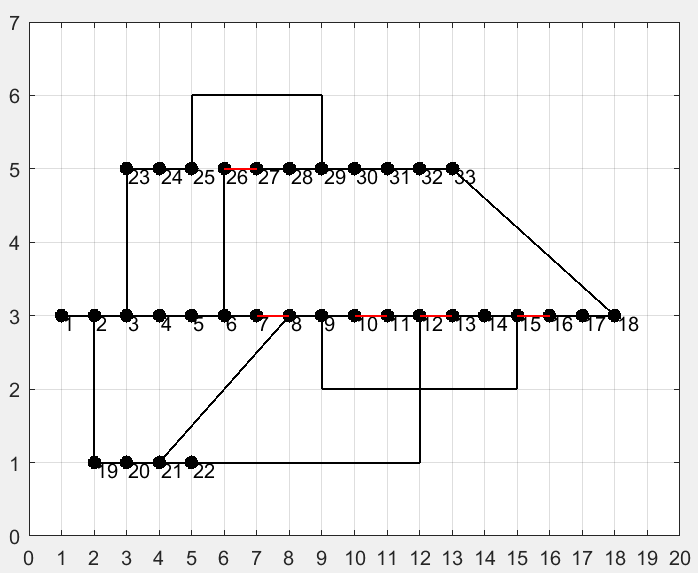
经验证(见结果图最后一张),该种约束方式下能够保证网络的连通性和辐射性。
需求响应约束:
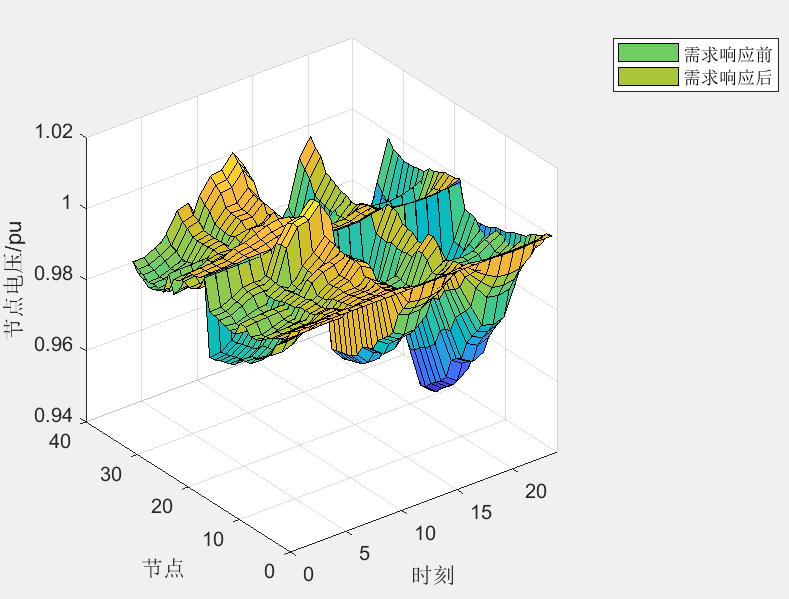
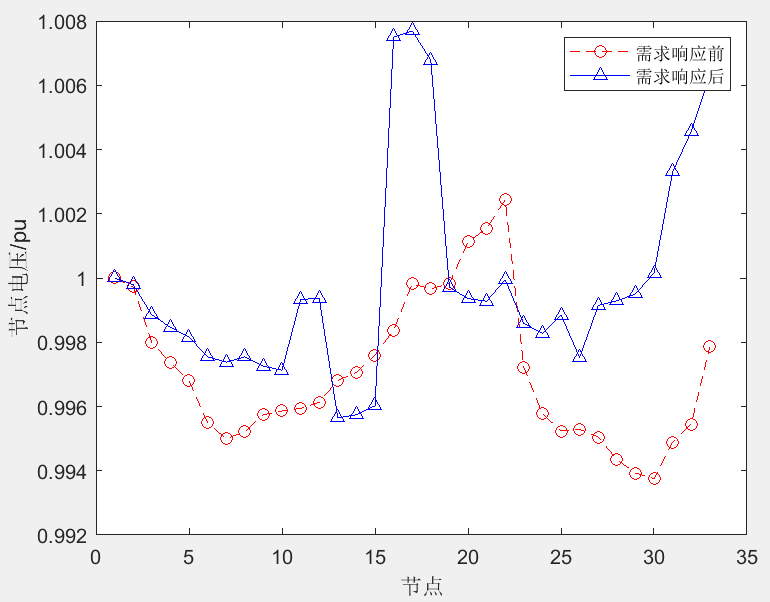
在配电网中采用需求响应策略,可以在降低负荷峰谷差的同时,减少配电网运行的综合成本,提高配电网运行的经济性和可靠性。
在该模型中,电价弹性系数为已知量,需求响应前后总负荷保持一致。
2部分代码
%% 系统参数mpc = IEEE33;% 风光负荷曲线P_wind0=[0.21 0.07 0.11 0.21 0.38 0.42 0.12 0.19 0.22 0.47 0.55 0.71 0.80 0.99 0.89 0.99 0.99 0.98 0.99 0.99 0.98 0.77 0.61 0.19];P_pv0=[0 0 0 0 0.17 0.24 0.40 0.54 0.60 0.51 0.35 0.29 0.27 0.25 0.18 0.10 0.06 0 0 0 0 0 0 0];P_L0=[0.37 0.33 0.31 0.28 0.27 0.28 0.28 0.27 0.26 0.24 0.30 0.76 0.82 0.86 0.76 0.54 0.43 0.65 0.81 0.95 0.99 0.91 0.65 0.19];nb=33; % 节点数ns=1; % 电源节点数nl=37; % 支路数n_pv=2; % 光伏数n_wind=3; % 风机数n_ess=2; % 储能数T=24; % 调度时段总数F=0.6; % 渗透率P_DG=sum(mpc.bus(:,3))*F/mpc.baseMVA/5; % DG额定容量P_wind_max=P_DG*P_wind0; % 风机最大有功P_pv_max=P_DG*P_pv0; % 光伏最大有功P_load=mpc.bus(:,3)/mpc.baseMVA*P_L0; % 有功负荷Q_load=mpc.bus(:,4)/mpc.baseMVA*P_L0; % 无功负荷Sij_max=15/mpc.baseMVA; % 支路功率最大值r_ij=mpc.branch(:,3)*ones(1,T); % 线路电阻x_ij=mpc.branch(:,4)*ones(1,T); % 线路电抗wind=[9 25 32]; % 风机接入位置pv=[17 22]; % 光伏接入位置ess=[7 25]; % 储能接入位置Umax=[1;1.06*1.06*ones(32,1)]; % 电压上限的平方Umin=[1;0.94*0.94*ones(32,1)]; % 电压下限的平方I_max=10; % 电流上限值P_ch_max=0.2/mpc.baseMVA; % 充电功率上限0.2MWP_dis_max=0.2/mpc.baseMVA; % 放电功率上限0.2MWE_min=0.15/mpc.baseMVA; % 储能容量下限0.15MWhE_max=0.8/mpc.baseMVA; % 储能容量上限0.8MWhn_ch=0.9; % 充电效率为0.9n_dis=0.85; % 放电效率为0.85E0=0.3/mpc.baseMVA; % 初始荷电状态为0.3MWhQ_CB_st=0.15/mpc.baseMVA; % 单个电容器无功补偿容量0.15MvarN_CB_max=5; % 最大可投切电容器数目ksai=0.5; % 弹性系数c1=3; % 网络损耗成本系数3元/kWhc2=1.2; % 弃风弃光惩罚系数1.2元/kWhc3=15; % 分段开关操作惩罚成本系数15元/次rho=zeros(1,24); % 分时电价rho([12:15,19:23])=1.026; % 峰时电价rho([7:11,16:18])=0.691; % 平时电价rho([1:6,24])=0.2561; % 谷时电价rho0=0.35; % 初始节点电价为0.35元/kWhM=1.1*1.1 - 0.9*0.9; % 中间变量P_g_max=10/mpc.baseMVA; % 电源有功功率最大值Q_g_max=10/mpc.baseMVA; % 电源无功功率最大值branch_to_node=zeros(nb,nl); % 流入节点的支路branch_from_node=zeros(nb,nl); % 流出节点的支路for k=1:nlbranch_to_node(mpc.branch(k,2),k)=1; %举例说明,k=1,流入节点2是支路1;同时流出节点1的是支路1;同理,k=2,流入节点3且流出节点2的是支路2;这一步建立支路和节点的连接关系branch_from_node(mpc.branch(k,1),k)=1;end%% 优化变量alpha_ij=binvar(nl,1); % 支路开断情况U_i=sdpvar(nb,T); % 电压的平方I_ij=sdpvar(nl,T); % 电流的平方P_ij=sdpvar(nl,T); % 线路有功功率Q_ij=sdpvar(nl,T); % 线路无功功率P_wind=sdpvar(n_wind,T); % 风机输出功率P_pv=sdpvar(n_pv,T); % 光伏输出功率Q_wind=sdpvar(n_wind,T); % 风机输出功率Q_pv=sdpvar(n_pv,T); % 光伏输出功率P_ch=sdpvar(n_ess,T); % 储能充电功率P_dis=sdpvar(n_ess,T); % 储能充电功率y_ch=binvar(n_ess,T); % 储能充电状态y_dis=binvar(n_ess,T); % 储能放电状态E_ESS=sdpvar(n_ess,T); % 储能荷电状态N_CB=intvar(1); % 投切的电容器数量P_cur=sdpvar(nb,T); % 需求响应后的负荷量P_g=sdpvar(nb,T); % 节点注入有功Q_g=sdpvar(nb,T); % 节点注入无功P_g_dot=sdpvar(nb,1); % 虚拟电源P_L_dot=ones(nb,1); % 虚拟负荷P_ij_dot=sdpvar(nl,1); % 虚拟功率%% 约束条件Constraints = [];%% 1.潮流约束m_ij=(1-alpha_ij)*M*ones(1,T);Constraints = [Constraints, P_g-P_cur+branch_to_node*P_ij-branch_to_node*(I_ij.*r_ij)-branch_from_node*P_ij == 0];Constraints = [Constraints, Q_g-Q_load+branch_to_node*Q_ij-branch_to_node*(I_ij.*x_ij)-branch_from_node*Q_ij == 0];Constraints = [Constraints,U_i(mpc.branch(:,1),:)-U_i(mpc.branch(:,2),:)<= m_ij + 2*r_ij.*P_ij + 2*x_ij.*Q_ij - ((r_ij.^2 + x_ij.^2)).*I_ij];Constraints = [Constraints,U_i(mpc.branch(:,1),:)-U_i(mpc.branch(:,2),:)>= -m_ij + 2*r_ij.*P_ij + 2*x_ij.*Q_ij - ((r_ij.^2 + x_ij.^2)).*I_ij];for k=1:nlfor t=1:TConstraints = [Constraints, cone([2*P_ij(k,t) 2*Q_ij(k,t) I_ij(k,t)-U_i(mpc.branch(k,1),t)],I_ij(k,t)+U_i(mpc.branch(k,1),t))];endendConstraints = [Constraints, Sij_max^2*alpha_ij*ones(1,T) >= P_ij.^2+Q_ij.^2];Constraints = [Constraints, I_max.^2.*alpha_ij*ones(1,T) >= I_ij , I_ij >= 0];Constraints = [Constraints, Umin*ones(1,T) <= U_i,U_i <= Umax*ones(1,T)];%% 2.拓扑约束Constraints = [Constraints , sum(alpha_ij) == nb-ns];Constraints = [Constraints , P_g_dot(2:33) == 0 , P_g_dot(1) <= nb];Constraints = [Constraints , P_g_dot-P_L_dot+branch_to_node*P_ij_dot-branch_from_node*P_ij_dot == 0];%% 3.DG功率约束Constraints = [Constraints , P_pv >= 0 , P_wind >= 0];Constraints = [Constraints , P_pv <= ones(n_pv,1)*P_pv_max , P_wind <= ones(n_wind,1)*P_wind_max];%% 4.储能约束Constraints = [Constraints , P_ch >= 0 , P_dis >= 0 , y_ch+y_dis <= 1];Constraints = [Constraints , P_ch <= y_ch*P_ch_max , P_dis <= y_dis*P_dis_max];Constraints = [Constraints , E_ESS(:,1) ==n_ch*P_ch(:,1)-1/n_dis*P_dis(:,1)+E0];Constraints = [Constraints , E_ESS >= E_min , E_ESS <= E_max];for t=2:TConstraints = [Constraints , E_ESS(:,t) ==n_ch*P_ch(:,t)-1/n_dis*P_dis(:,t)+E_ESS(:,t-1)];
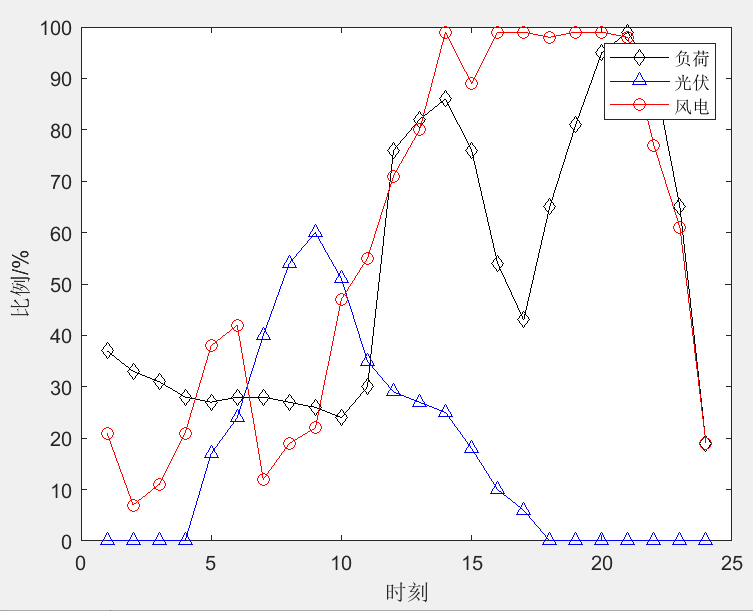
3程序结果








![详解梯度下降从BGD到ADAM - [北邮鲁鹏]](https://img-blog.csdnimg.cn/043591377130437e907be8d9fc18275d.gif)