目录

1.数据归一化处理

2.数据标准化处理

3.Lasso回归模型

4.岭回归模型

5.评价指标计算

---

1.数据归一化处理

"""
x的归一化的方法还是比较多的我们就选取最为基本的归一化方法
x'=(x-x_min)/(x_max-x_min)
"""
import numpy as np
from sklearn.preprocessing import MinMaxScaler
rd = np.random.RandomState(1614) 
X =rd.randint(0, 20, (5, 5))
scaler = MinMaxScaler()#归一化
# 对数据进行归一化
X_normalized = scaler.fit_transform(X)
X_normalized

2.数据标准化处理

"""
标准化的方法x'=(x-u)/(标准差)
"""
import numpy as np
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
rd = np.random.RandomState(1614) 
X =rd.randint(0, 20, (5, 5))#X时特征数据
# 创建StandardScaler对象(标准化)
scaler = StandardScaler()
X_standardized = scaler.fit_transform(X)
X_standardized

  

3.Lasso回归模型

"""
lasso回归
"""
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.linear_model import Lasso
# 从Excel读取数据
dataframe = pd.read_excel('LinearRegression.xlsx')
data=np.array(dataframe)
X=data[:,0].reshape(-1,1)
Y=data[:,1]
# 创建Lasso回归模型
lambda_ = 0.1  # 正则化强度
lasso_reg = Lasso(alpha=lambda_)
# 拟合回归模型
lasso_reg.fit(X, y)
# 计算回归系数
coefficients = np.append(lasso_reg.coef_,lasso_reg.intercept_)
# 绘制散点图和拟合曲线
plt.figure(figsize=(8,6), dpi=500)
plt.scatter(X, y,  marker='.', color='b',label='Data Points',s=64)
plt.plot(X, lasso_reg.predict(X), color='r', label='Lasso Regression')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Lasso Regression')
plt.legend()
plt.text(x=-0.38,y=60,color='r',s="Lasso Regression Coefficients:{}".format( coefficients))
plt.savefig(r'C:\Users\Zeng Zhong Yan\Desktop\Lasso Regression.png')
plt.show()

  

4.岭回归模型

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.linear_model import Ridge# 从Excel读取数据
dataframe = pd.read_excel('LinearRegression.xlsx')
data=np.array(dataframe)
X=data[:,0].reshape(-1,1)
Y=data[:,1]
#创建岭回归模型
lambda_ = 0.1  # 正则化强度
ridge_reg = Ridge(alpha=lambda_)
#拟合岭回归模型并且计算回归系数
ridge_reg.fit(X, y)
coefficients = np.append(ridge_reg.coef_,ridge_reg.intercept_)
#绘制可视化图
plt.figure(figsize=(8, 6), dpi=500)
plt.scatter(X, y,  marker='.', color='b',label='Data Points',s=64)
plt.plot(X, ridge_reg.predict(X), color='r', label='Ridge Regression')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Ridge Regression')
plt.legend()
plt.text(x=-0.38,y=60,color='r',s="Ridge Regression Coefficients:{}".format(coefficients))
plt.savefig(r'C:\Users\Zeng Zhong Yan\Desktop\Ridge Regression.png')
plt.show()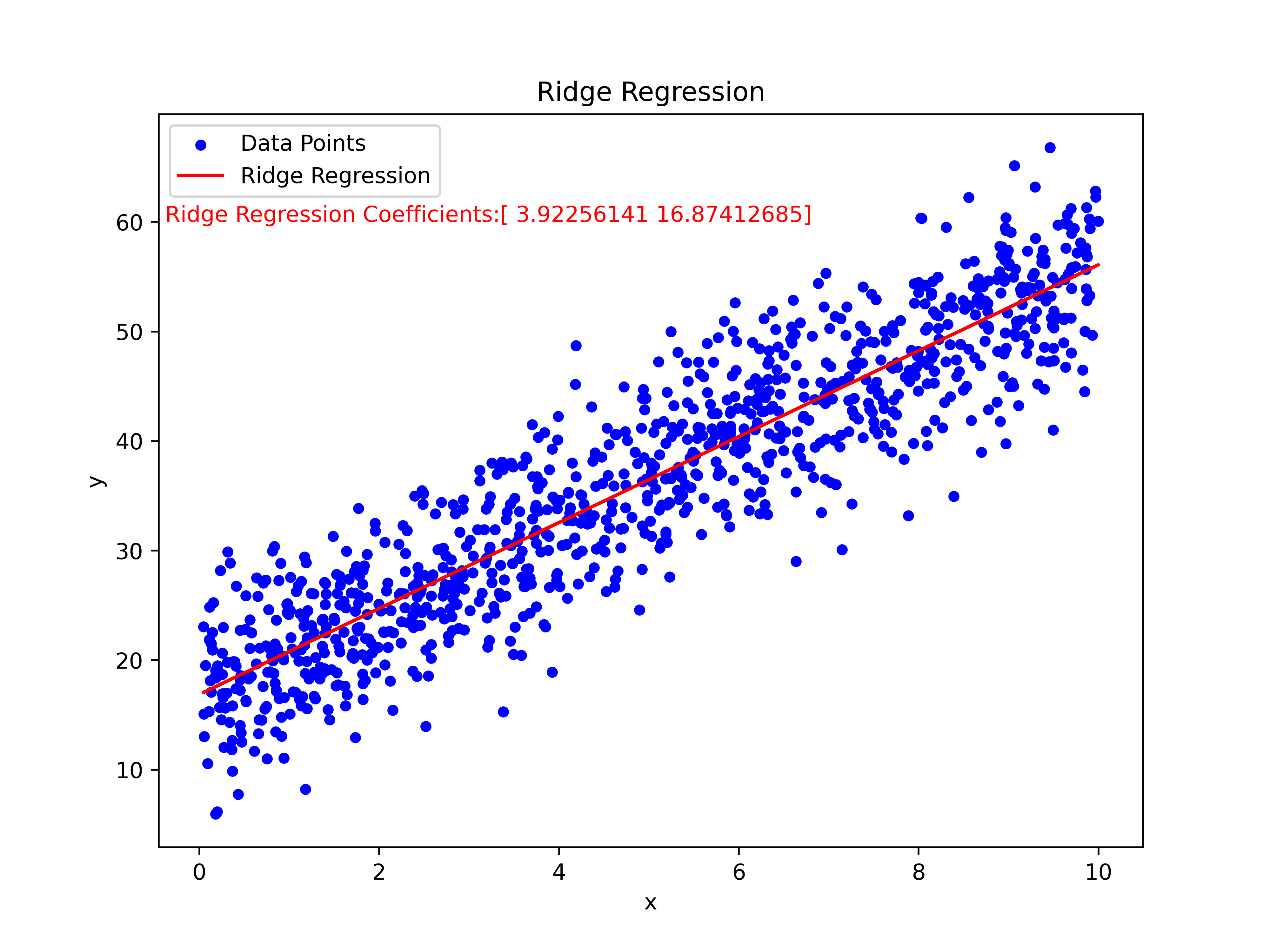

5.评价指标计算

MSE=i=1n(Yi-Y^)2nRMES=i=1n(Yi-Y^)2nMAE=i=1n|Yi-Y^|nR2=1-i=1n(Y^-Yi)2i=1n(Y¯-Yi)2

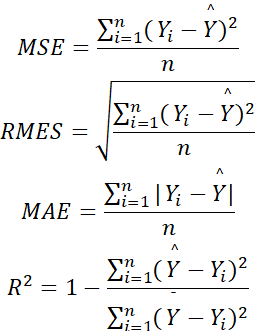
#4种误差评价指标
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
# 预测值
y_pred = ridge_reg.predict(X)
# 计算均方误差（MSE）
MSE = mean_squared_error(y, y_pred)
# 计算均方根误差（RMSE）
RMSE= np.sqrt(mse)
# 计算平均绝对误差（MAE）
MAE= mean_absolute_error(y, y_pred)
# 计算 R 方（决定系数）
R_squre = r2_score(y, y_pred)
print("均方误差:", MSE )
print("均方根误差:", RMSE)
print("平均绝对误差:", MAE)
print("R方误差系数:", R_squre)